求离散点的曲率

 例1.

clc;clear;close all;
x0 = linspace(0.1,2,100);%x0,y0验证函数离散点，可以非等间隔
y0 = 1./x0;
h1 = abs(diff([x0])) ;
h = [h1 h1(end)];
ht = h;
yapp1 = gradient(y0)./ht; %matlab数值近似
yapp2 = del2(y0)./ht; %matlab数值近似
k2 = abs(yapp2)./(1+yapp1.^2).^(3/2);
figure(2);hold on;plot(k2)
figure(2);hold on;title('曲率曲线')
[~,maxFlag] = max(k2);%曲率最大位置
x_max = x0(maxFlag);
y_max = y0(maxFlag);
%画出图像 标注曲率最大点
figure(1);hold on;plot(x0,y0,'.-');
figure(1);hold on;plot(x_max,y_max,'rp')
title('标注最大曲率点')
xlabel('log10((norm(B*Xk-L)))')
ylabel('log10((norm(Xk)))')

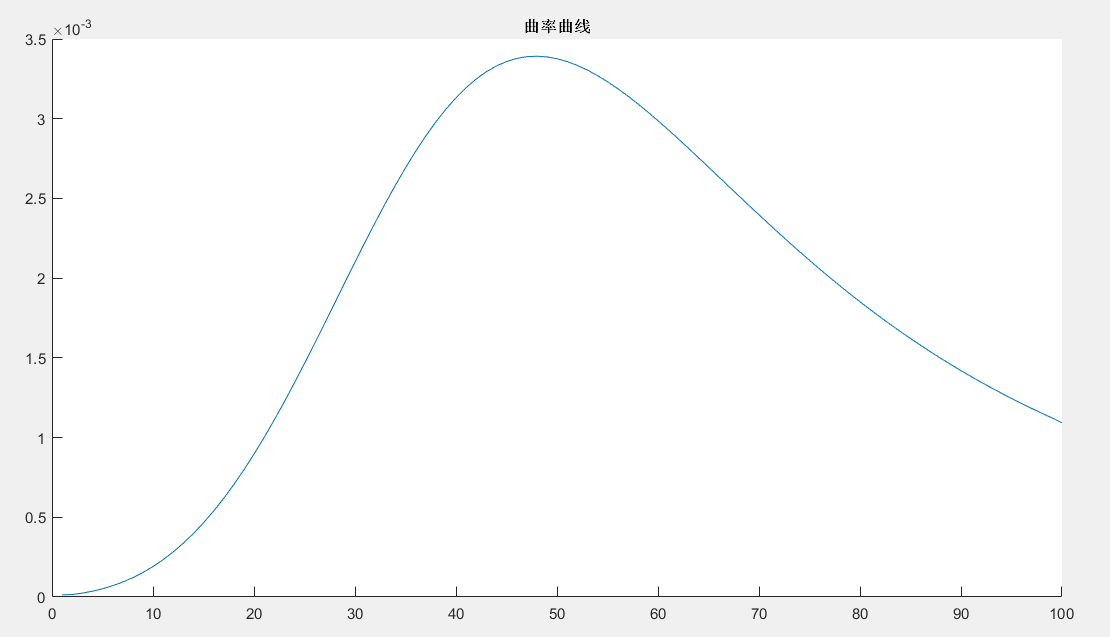
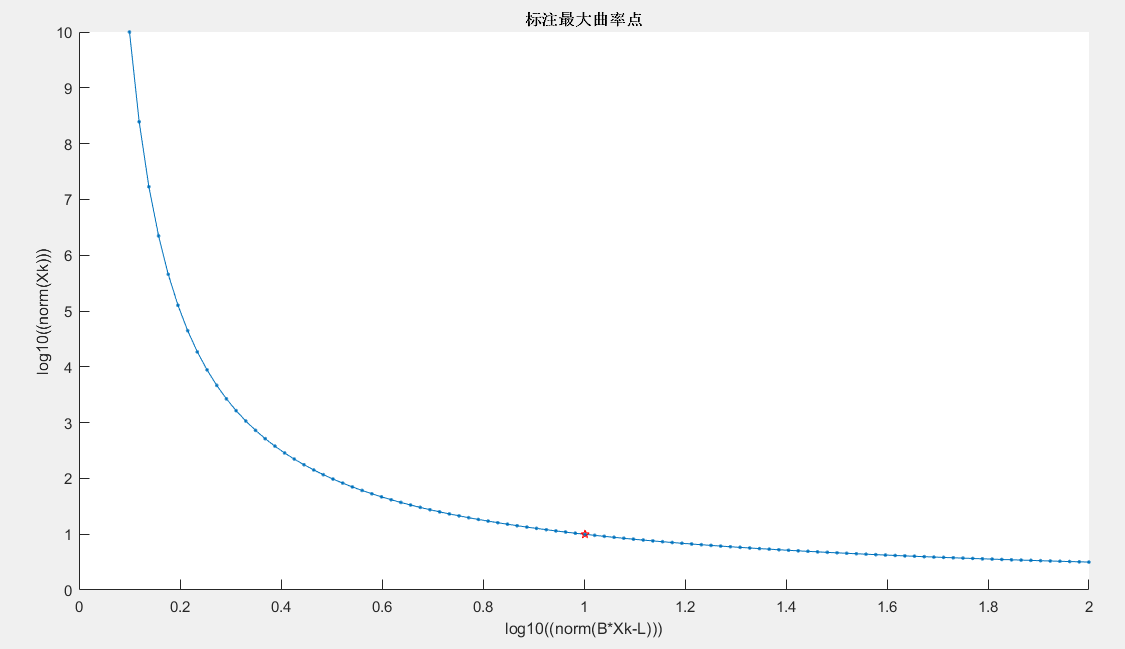
来源：https://blog.csdn.net/xiaoxiao133/article/details/77916363

---

 例2

clc;
clear;
close all;
x0 = 0 : 0.1 : 2 * pi;
y0 = sin(x0).*cos(x0);
figure(1);plot(x0,y0,'r-');
h = abs(diff([x0(2), x0(1)]));

%一阶导
ythe1 = cos( x0 ) .^2 - sin(x0).^2; %理论一阶导
yapp1 = gradient(y0, h); %matlab数值近似
figure(2);
hold on;
plot(x0, ythe1, '.');
plot(x0, yapp1, 'r');
legend('理论值', '模拟值');
title('一阶导');

%二阶导
ythe2 = (-4) * cos(x0) .* sin(x0); %理论二阶导
yapp2 = 2 * 2 * del2(y0, h);       %matlab数值近似

figure
hold on;
plot(x0, ythe2,'.');
plot(x0, yapp2,'r');
legend('理论值', '模拟值');
title('二阶导');

% 模拟曲率
syms x y
y = sin(x) * cos(x);
yd2 = diff(y, 2);
yd1 = diff(y, 1);
k = abs(yd2) / (1+yd1^2)^(3/2);  %% 曲率公式
k1 = subs(k, x, x0);
k2 = abs(yapp2)./(1+yapp1.^2).^(3/2);

figure
hold on;
plot(x0, k1, '.');
plot(x0, k2, 'r');
legend('理论值', '模拟值');
title('曲率');

　

 来源：https://blog.csdn.net/q1302182594/article/details/50545361

---

 例3

https://zhuanlan.zhihu.com/p/72083902