adam优化算法

1.SGD的难处：

考虑z=1/20*x²+y²图像，

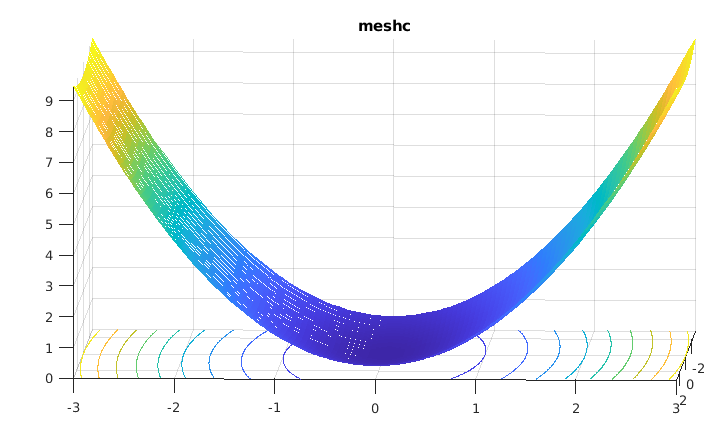
等高线图和负梯度方向：

假设从（-7,2）这一点开始进行梯度更新（下降）：

learningrate=0.9;

x-=0.9*(1/10)*x   (1)

y-=0.9*2*y          (2)

把（-7,2）这一点带入（1）和（2）式中，得到一个新的(x,y)，继续带入，可以得到一个x的列表和y的列表，这个列表代表了梯度下降的路线。

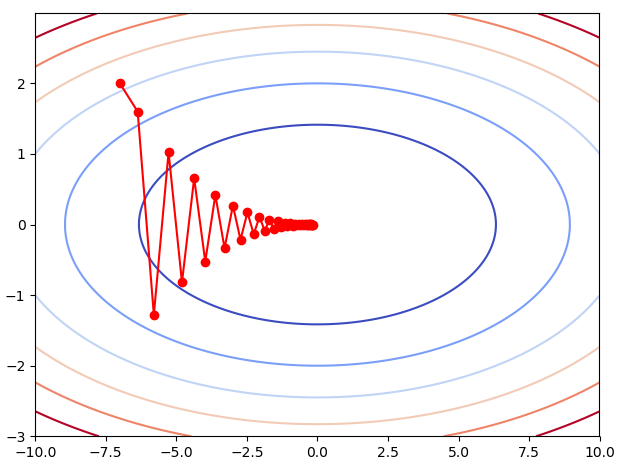
假设走40步，梯度下降的路线如图所示：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x_sgd=[-7.0]
y_sgd=[2.0]
x=-7.0
y=-2.0
N=40
lr=0.9
for i in range(N):
    x-=x/10*lr
    y-=2*y*lr
    x_sgd.append(x)
    y_sgd.append(y)
def f(x,y):
    return np.power(x,2)/20+np.power(y,2)
x=np.arange(-10,10,0.01)
y=np.arange(-3,3,0.01)
x,y=np.meshgrid(x,y)
plt.plot(x_sgd,y_sgd,color='red',marker='o',linestyle='solid')
plt.contour(x,y,f(x,y),cmap=plt.cm.coolwarm)
plt.show()

 或者：

clc;
clear;
close all;


[xx,yy]=meshgrid(-10:0.1:10,-3:0.1:3);
zz=xx.^2/20 + yy.^2;
%zz=(1/20)*xx.^2 + yy.^2;
figure(6);surfc(xx,yy,zz);
figure(7);h=contour(xx,yy,zz, 50);
%clabel(h);
%[dx, dy]=gradient(zz,.2,2);
[dx, dy]=gradient(zz,.1,.1);
hold on;
%quiver(-dx, -dy);


lr=0.9;
a=[];
b=[];
x=-7;
y=2;
for i=1:40
    a=[a,x];
    b=[b,y];
    x=x-lr*(1/10)*x;
    y=y-lr*2*y;
    if i>40
        break
    end       
end
figure(6);hold on;plot(a,b,'r.-');
figure(7);hold on;plot(a,b,'r.-');

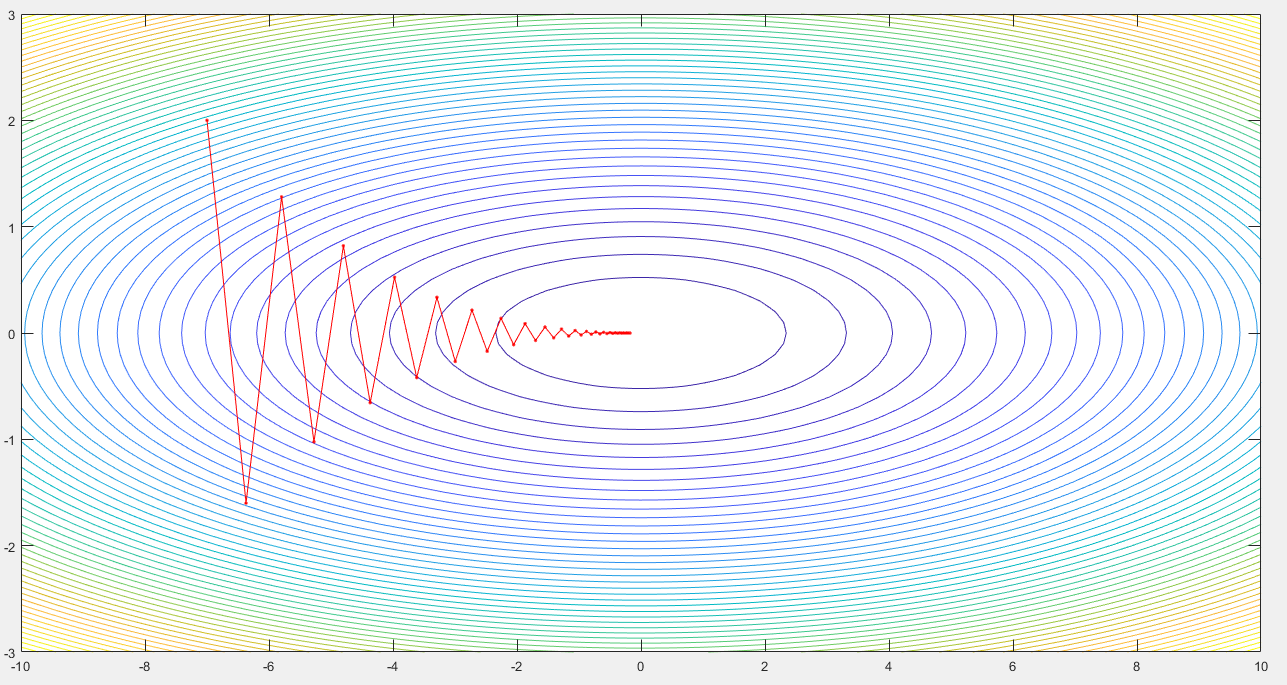
 所以SGD的困难在于：梯度下降的方向不是朝着坑的最低点移动，而是“之”字形向最低点移动，或者称之为“蛇形移动”。

解决之法：Momentum

（1）

 （2）

B代表MiniBatch，指参数在一个小批量中更新。

是（待更新）的模型参数，当=0的时候，式子（2）是：

 ，就变成了一般的SGD梯度下降。

 把式子（1）变形一下：

（3）

（3）

这是个很优美的形式。

（3）式的另一个观察视角：

 （4）

对于（4）式：

 y⁽²⁰⁾是对过去的时刻的值，做一个指数加权平均，越是离的近的时刻的值，起的作用越大，越是过去久远的时刻的值，起的作用越小。

 

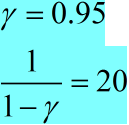
 这对我们有什么帮助呢？观察下图，注意到大部分的梯度更新呈锯齿状。我们也注意到，每一步的梯度更新方向可以被进一步分解为 w1 和 w2 分量。如果我们单独的将这些向量求和，沿 w1 方向的的分量将抵消，沿 w2 方向的分量将得到加强。

 

2.adagrad algrithm（adaptive gradiant algrithm）
自适应梯度下降算法，这种算法随着时间的增加，学习率会逐渐降低，就是说越靠近最小值的时候，步子越是小心。

 

圆圈里面一个点代表按照元素相乘，如=（4,9），=（16,81），代表对过往梯度和的累加。