三、行列式的逆序数法定义（行列式的第二种定义）
1. 排列和逆序
由n个数1,2,3，...n组成的一个有序数组成为一个n级排列，如2,3，1,4,5是一个5级排列，1,2,3,4,5也是一个5级排列，n级排列共有n！个，如，5级排列共有5！=120个。
逆序： 在一个n级排列i1,i2,i3,...is,...it,...in中，is>it ,且is 排在前面，则这两个数构成一个逆序。
比如6级排列：6 2 1 5 3 4 ，
6 2，6 1， 6 5 ，6 3 ， 6,4构成了5对逆序。只要前大后小，就构成一对逆序。
2 1 构成了1对逆序 1 5， 1 3， 1 4都是顺序，不是逆序。
5 3 ， 5 4 构成了2对逆序
逆序数：给定一个排列，逆序的总数称为逆序数，记作τ，如τ(6 2 1 5 3 4)=5+1+2=8, 即排列6 2 1 5 3 4的逆序数是8. 由小到大的排列称为自然排序，如1 2 3 4 5 ，显然，自然排序的逆序数是0，因为都是前小后大。
奇排列和偶排列： τ是一个排列的逆序数，τ为奇数的排列称为奇排列，τ为偶数的排列称为偶排列。τ(6 2 1 5 3 4)=8，所以排列6 2 1 5 3 4是偶排列。
2. n阶行列式的定义
n阶行列式（以5阶为例）：
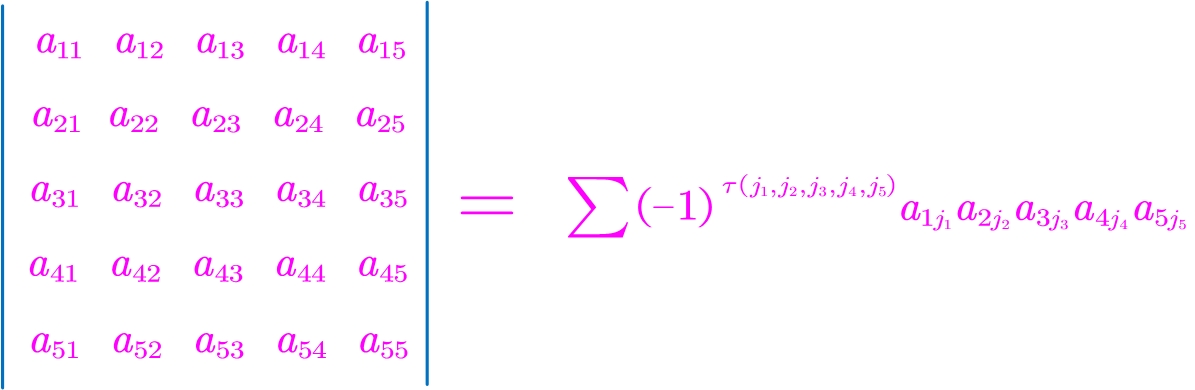
1,2,3,4,5是行下标（已顺排）。
j1,j2,j3,j4,j5是列下标。
表示对所有n(5)个列下标排列求和，故为n!(5!)项之和，注意到行下标已经顺序排列，而列下标是5级排列中的任意一个排列，所以每项由不同行、不同列的n个(5个)元素乘积组成，每项的正负号取决于(-1)τ(j1,j2,j3,j4,j5) ,当列下标为奇排列时，为负号，为偶排列时，取正号。
举例：
确定5阶行列式展开后某一项a12a31a54a43a25的符号。
解答：
a. 含有5个元素，所以行列式必定是5阶行列式，展开后总共应该是120项。
b. 把行下标进行顺序排列：a12a25a31a43a54
c. τ(2 5 1 3 4)=4
所以，符号是正号。
2阶行列式的逆序数法定义(总共有2!=2项)：
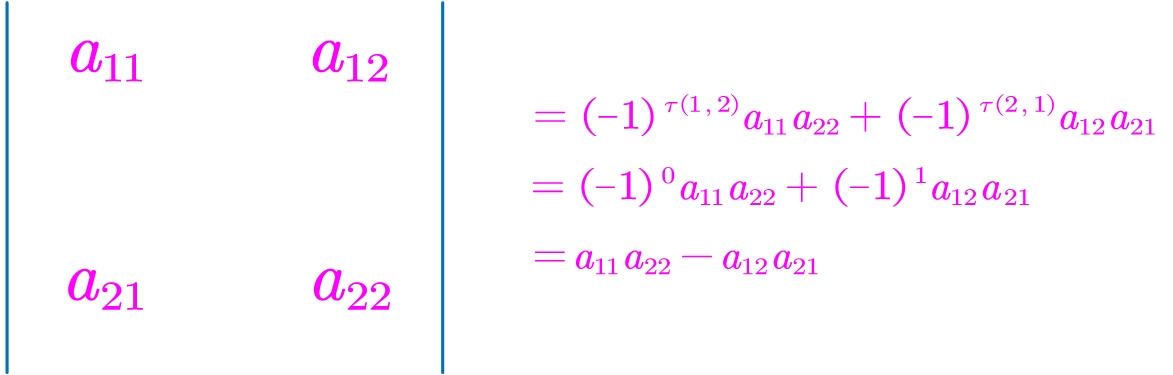
3阶行列式的逆序数法定义(总共有3!=6项)：
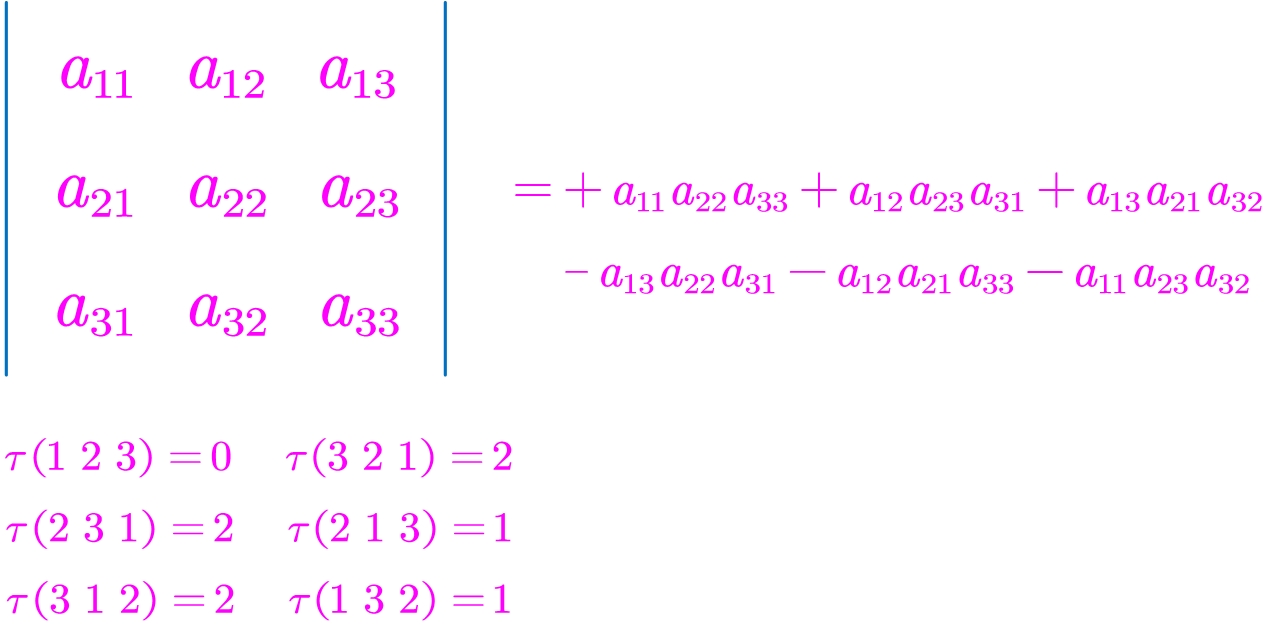
行列式表白：
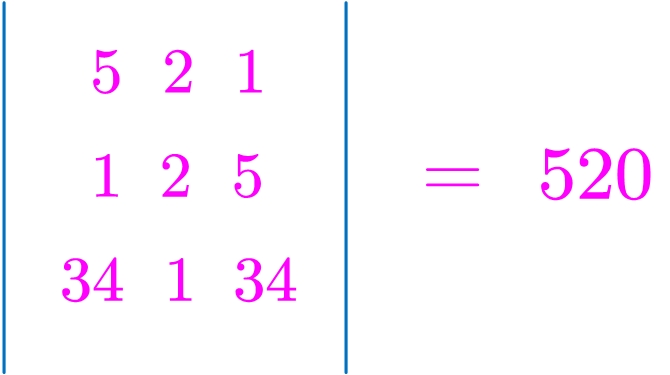
四、行列式的展开定理（行列式的第三种定义，本质：降阶）
注：行列式的第一种定义是柯西给出的面积定义(柯西给出的行列式的测度定义)，即具有几何意义的定义。
阶数超过3阶的行列式，若还用“一”、“三”的方法，就太麻烦了(如5阶行列式有120项)，所以，提出行列式的展开定理。
1.余子式
在n 阶行列式中，去掉元素aij所在的第i行，第j列元素，剩下的元素按原来的位置组成的n-1阶行列式称为元素aij的余子式，记作Mij,举例：
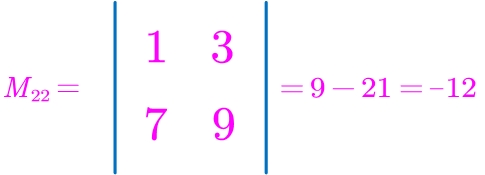
2.代数余子式
余子式乘以(-1)i+j后称为元素aij的代数余子式。记作：Aij
Aij=(-1)i+jMij
显然也有：
Mij=(-1)i+jAij
所以，余子式和代数余子式之间只差一个符号。
注意，余子式首先是行列式，其次是一个数，代数余子式是一个数。
举例：
3.行列式按某一行（列）展开：
行列式的值等于行列式的某行（列）的元素分别乘以其相应的代数余子式后再求和。即
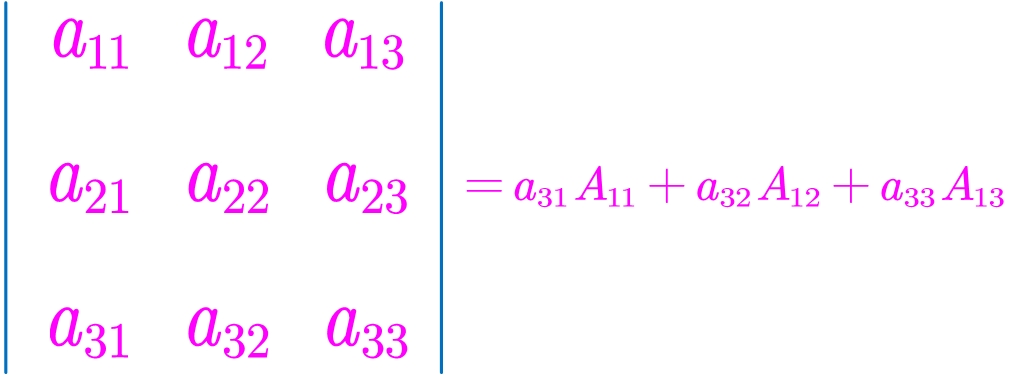
行列式按行展开的本质是降阶：把一个n(3)阶写成n(3)个n-1(2)阶。
如果某一行的元素有很多是0，就相当于项数减少很多。
但：行列式的某行（列）元素分别乘以另一行（列）元素的代数余子式后再求和，结果是0.
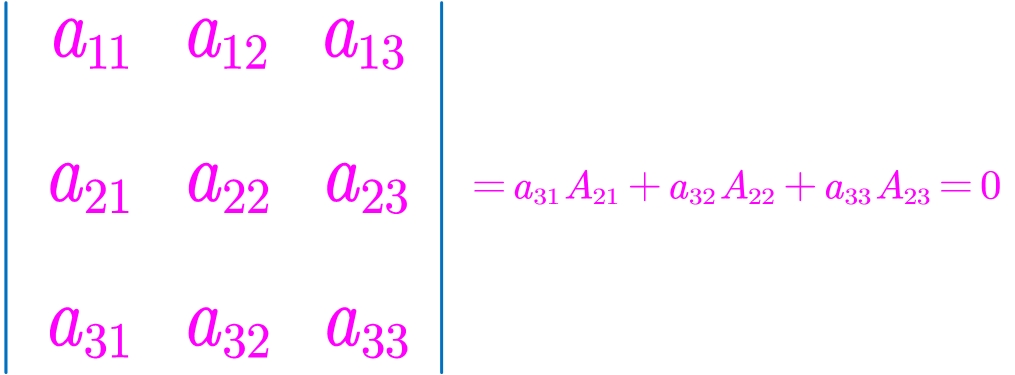
五、几个重要的行列式
1.主对角线行列式（右上（左下）三角行列式）
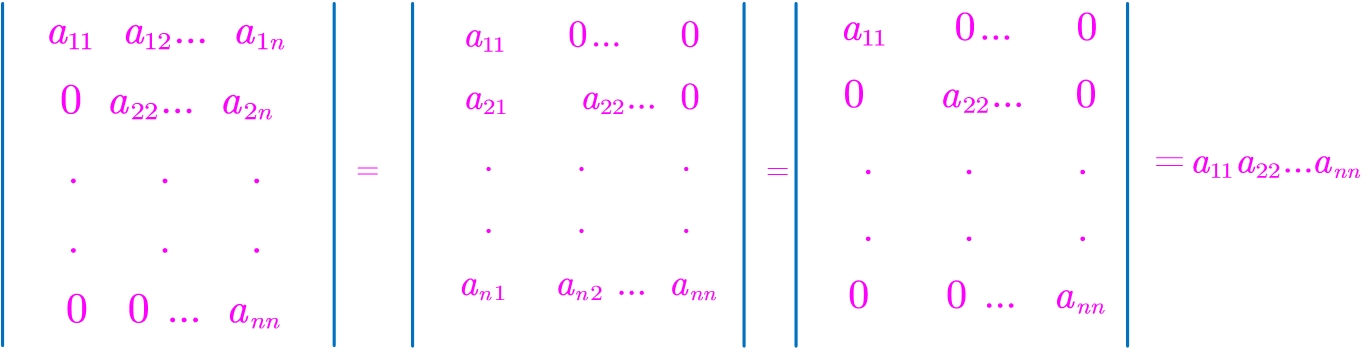（按行列式的第二种定义计算）
2.副对角线行列式
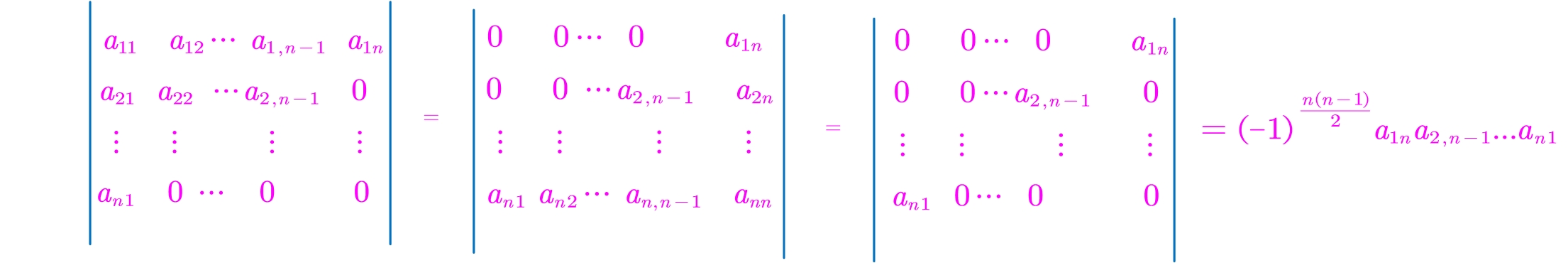（按行列式的第二种定义计算）
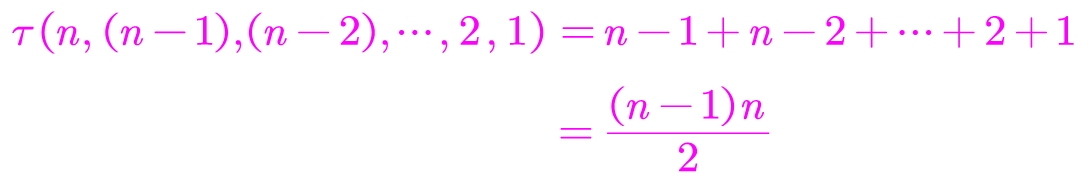
3.拉普拉斯展开式
A为m阶矩阵，B为n阶矩阵，O为0矩阵，则：
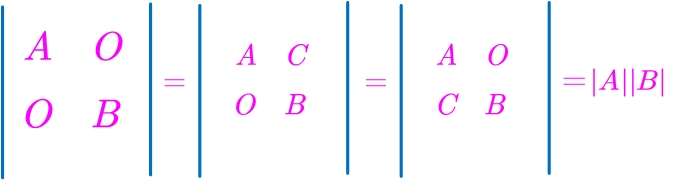
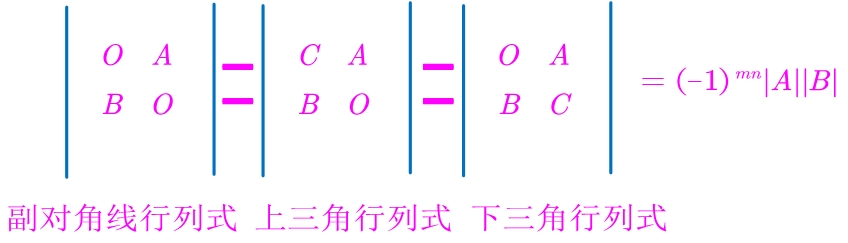
为何要加个-1的m*n次方？因为下面的副对角线行列式转换成上面的主对角线行列式交换行的次数是m*n次。
4. n阶范德蒙德行列式
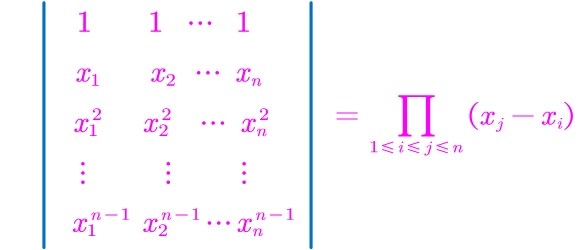
可以用数学归纳法证明这个结果。
例如：3阶方德蒙德行列式：
有1、2、3年级的学生，高年级要欺负所有低年级，所以结果是：
（x3-x2）（x3-x1）（x2-x1）