P5 第二讲 矩阵01

 截图来自：https://www.bilibili.com/video/BV1iV411f7KD?p=5

注解：求矩阵逆的3中方法：

1. 定义法。
2. 伴随矩阵法。
3. 用初等变换求矩阵的逆。

• 矩阵的秩表示着矩阵最本质的特征。

 

 

 注解：

1. 子式一定是个行列式，是可以算的。
2. 某阶子式不具备唯一性。

 注解：

1. 2阶子式不为0，则这两个行向量(2,7)和(8,1)不平行，则意味着它们也线性无关。
2. 如果这个二阶子式的两个行向量再添加几个数:(1,2,5,7),(6,8，-3,1)，则它们同样不会平行，同样线性无关。
3. 如果一个n阶方阵的秩是n，则意味着组成这个矩阵的所有行向量线性无关，谁也表示不了谁，还意味着此矩阵的行列式不为0，还意为着方阵是可逆矩阵,此方阵称为满秩矩阵。例如，一个三阶方阵，如果秩是3,则意味着任意一个向量都无法用其它两个向量线性表示，任何两个向量也无法表示第三个向量，还意味着以这三个向量为棱所组成的平行六面体的体积不为0。

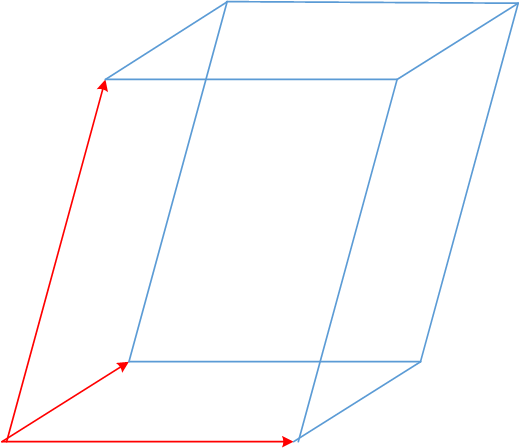
• 矩阵的秩本质就是组成该矩阵的线性无关的向量的个数，如果矩阵的秩是k,则意味着此矩阵最高阶非零子式的阶数是k阶，任何(k+1)阶子式都是0，则意味着该矩阵最多有k个线性无关的向量，如果再多一个，则矩阵的行列式就会为0.
• 矩阵的秩反应的是矩阵中各个行向量或者各个列向量之间某种客观的联系。(相关或无关)
• 矩阵的秩表明了矩阵中有多少个向量是线性无关的，这些个向量之间谁也表示不了谁。

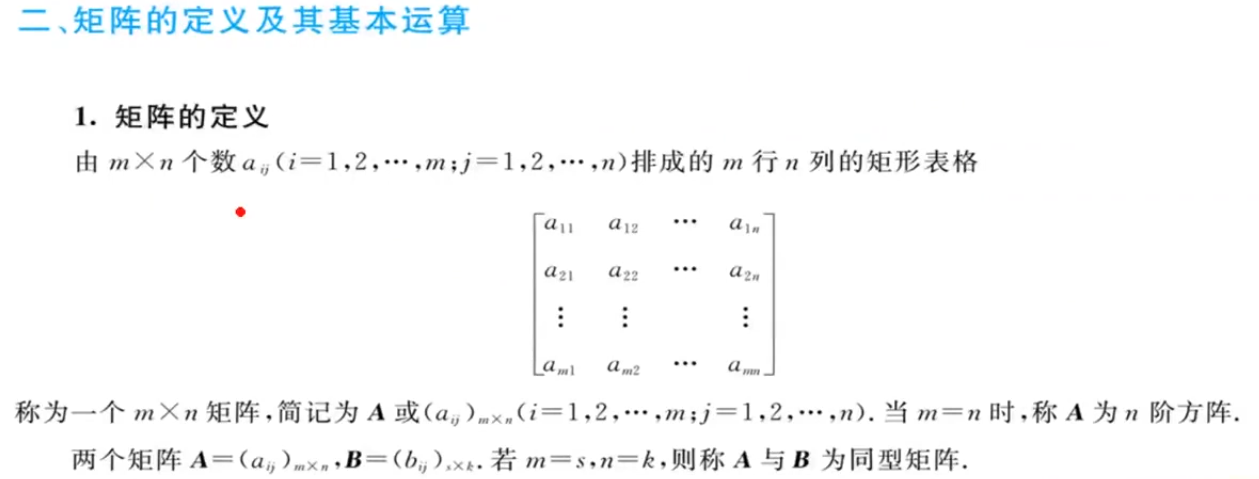
注解：

1. n阶方阵也叫n阶矩阵。

 

 

注解：

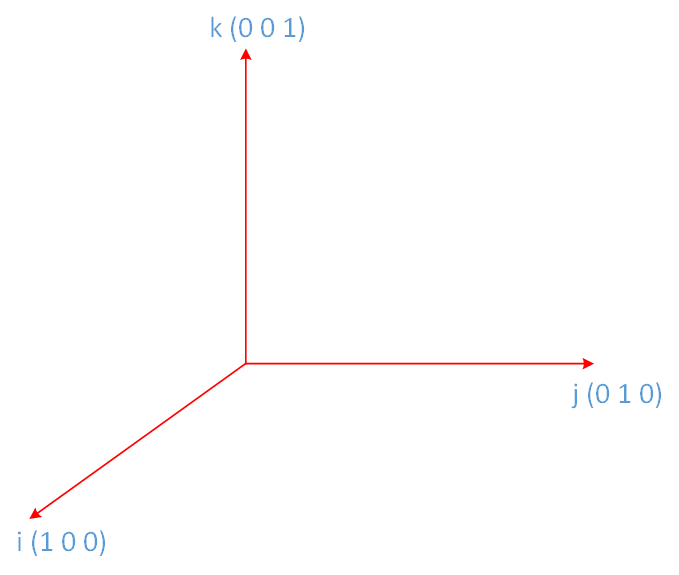
1. 标准正交向量组又叫规范正交基。
2. i=j的时候，模是1，就是说自己与自己的内积是1；i≠j的时候，内积是0，说明它们是正交的。
3. 标准正交向量组中每一个向量都是单位向量，且任意两个列向量都是正交的。
4. 下面的笛卡尔坐标系中的单位向量组：(i j k)就是一组标准正交基。