[Class]数值分析.王兵团.北京交通大学.全128讲[48:35:32]_哔哩哔哩_bilibili

插值与拟合是最早的数据挖掘的方法。
现在还有神经网络等手段。

问:什么函数最简单?
答:肯定是多项式了。
所有的插值函数都是建立在多项式函数的基础上的。插值函数有无穷多,那我就选择最简单的多项式函数。多项式函数只有+-*/ 可以用计算机来做。发展到后来,可以用三角函数,指数函数,对数函数进行插值。

4.2式有n+1个式子,
n+1个已知的插值点:(x0,y0),(x1,y1),(x2,y2)...(xn,yn)------->(n+1)个插值点意味着有n+1个插值条件
m次幂。
a在此处是待求参数,或者说是线性方程组的待求系数,a的幂次都是1次,所以是线性方程组。此线性方程组变量(未知数)的个数:m+1个:a0,a1,...am. 数据点的个数即方程的个数是n+1个。

下面是一个例子,用范德蒙行列式解线性方程组的例子:


注解:
1.此处的常数项是指y值。

下面的这个例子的来源是:(41条消息) 【线性代数(6)】范德蒙德行列式及克莱姆法则_lys_828的博客-CSDN博客_线性代数范德蒙德行列式

定理4.1说明了满足插值条件的插值多项式是存在的,下面还要说明这样的插值多项式还是唯一的。

注解:
1.两个插值多项式在n+1个插值节点上的值一定是相等的。
2.两个n次插值多项式,n次项系数一样的的话,那么相减后的插值多项式最多是n-1次。所以说小于等于n。
3.一个2次多项式有3个根,那这个多项式(函数)只能是恒等于0.连常数也不能是。
n次多项式最多有n个根,这是代数基本定理。
下面的事情:怎么去找出来这个存在且唯一的n次插值多项式?
按道理来说,解上面的那个线性方程组就行了,因为那个线性方程组有唯一解,把唯一解求出来就是要求的系数了。
但是,人们发现,方程组是病态的。何为病态?
答:系数变化一点,解就变化很大。下面这个图里面,这些系数都是会经常发生扰动的,扰动是经常会出现的。所以每个待求参数的值(有扰动的话,分子分母都在发生变化)都很容易发生变化。一发生扰动,就保证不了结果是准确的了。2阶的,3阶等低阶的问题还好,高阶的问题这种解法肯定是不行的了。
比如说,有个观测值(x20,y20)中的x20发生了0.1的变化,假如插值函数是3次的,那么行列式中的值就会发生0.001的变化,此时,行列式的值会发生很大的变化。

那怎么办呢?怎么解决直接解线性方程组无法抵抗病态这个事情呢?

注解:
1.a和b 应该是插值点两端的端点。
2.为何能外推呢?答:因为多项式函数的定义域是全体实数。
3.假如需要用现在的数据,去推断未来的数据,这个是必须要外推的。
拟合:
1.拟合问题里面的数据点可以是相同的。

拟合的思想:某个最大值最小!
假如用插值,那δ不就是0了吗?误差是0呀,等于没有误差,看起来插值比拟合好。但是,这些数据点有的不是互异的,所以不满足插值的前提条件。而且,一般拟合的数据点都带有误差,用带有误差的数据点去做插值,解的波动会很大(函数的波动性会很大)。要想去除波动性,用拟合比较好。
所以,插值和拟合解决问题的数据点是不一样的。区别如下:
1.插值问题的数据点没有重复,自变量是互异的。
2.拟合问题数据点的自变量不一定互异。拟合问题的定义里面就有:互异和不互异都行。
3.对于某些问题,插值和拟合差不多,有些问题,只能用其中的一种方法。

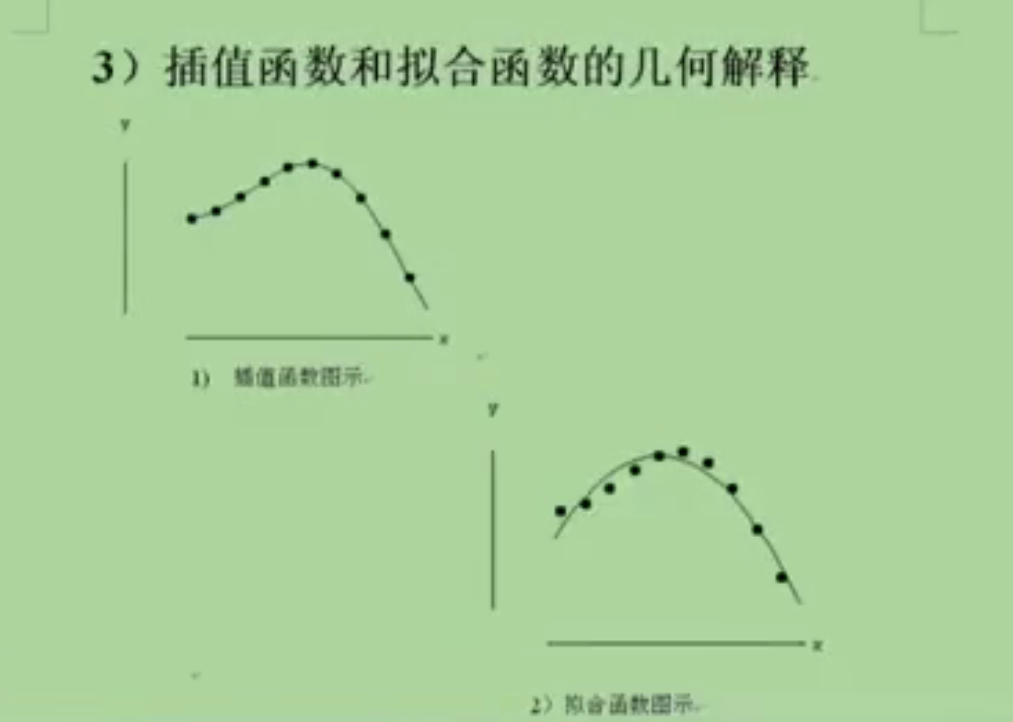
数据的波动比较大的情况,用拟合好一些。数据的波动不是特别大,用插值好一些。
为了对抗病态问题,下面看拉格朗日是怎么做的?(拉格朗日解决问题的办法叫做拉格朗日插值),自己设计了一套方法,越过解线性方程组,去找多项式。

拉格朗日的思想:求一个多项式的问题变成一堆多项式的线性组合的问题。表面上难,实际上不难。

无关的意思:插值的基函数和观测值无关。
最后一行黄色:把第k个插值节点带进去。等式最左边代表n次插值多项式,等式最右边是被插的值。
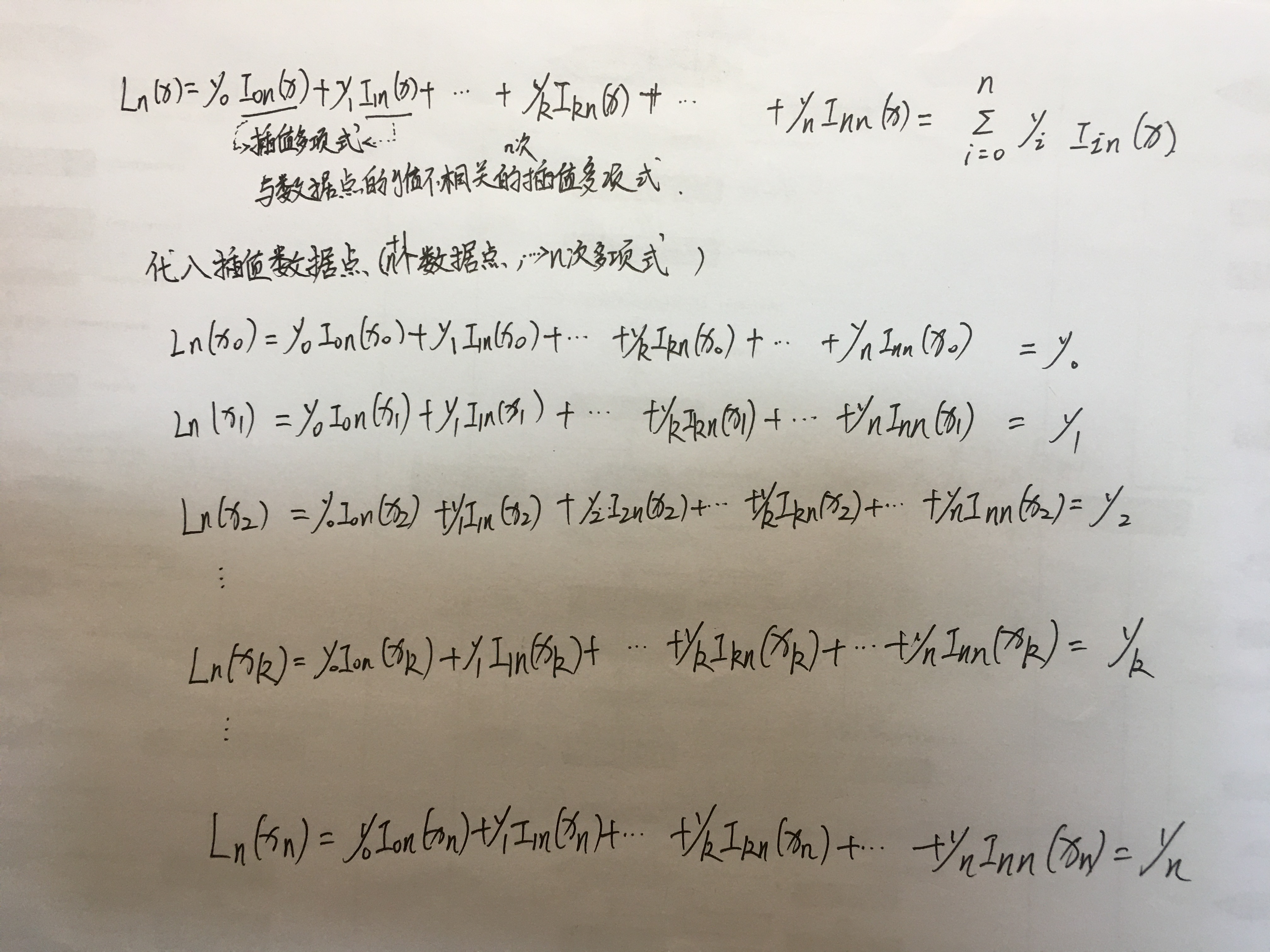



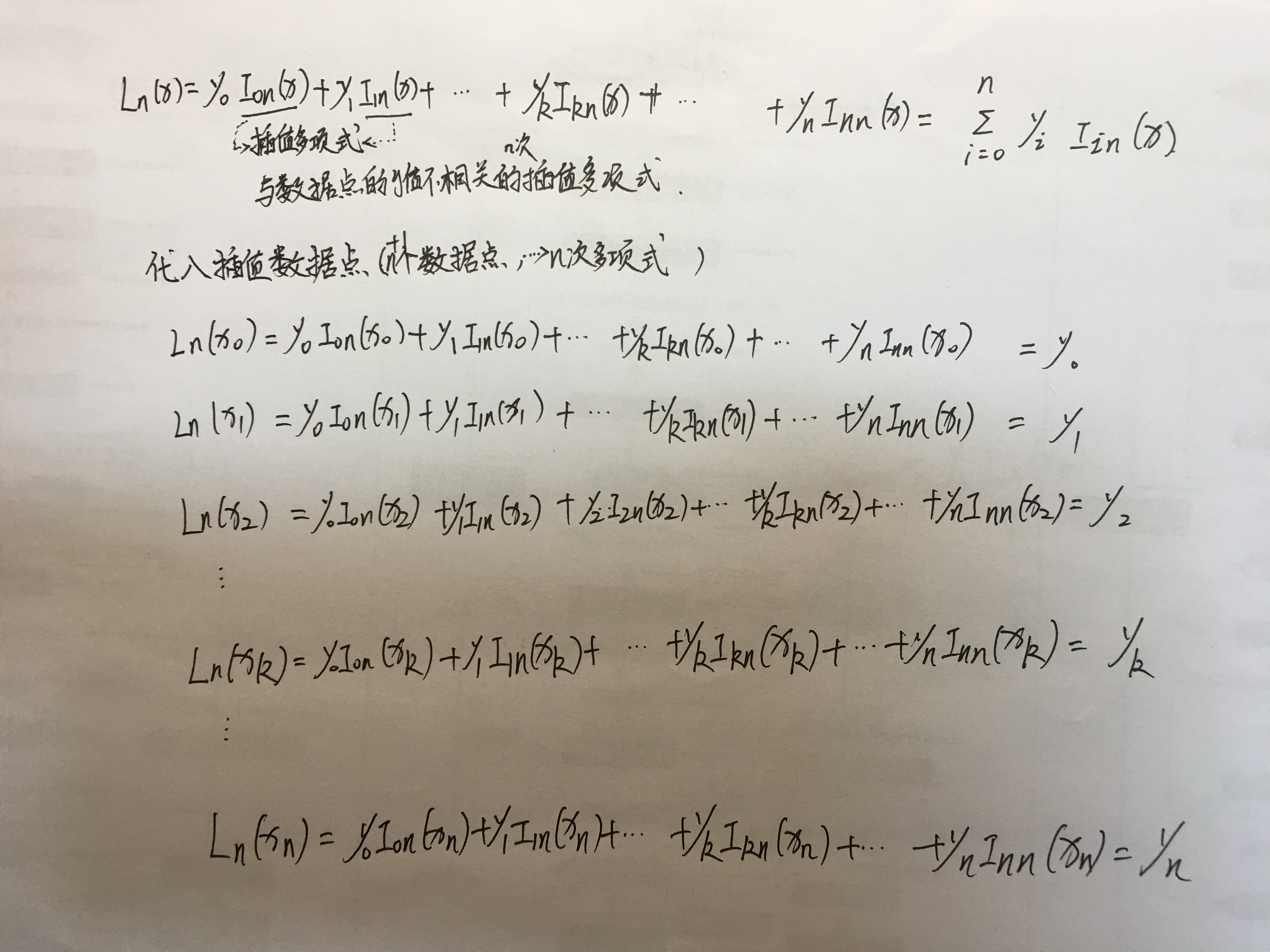
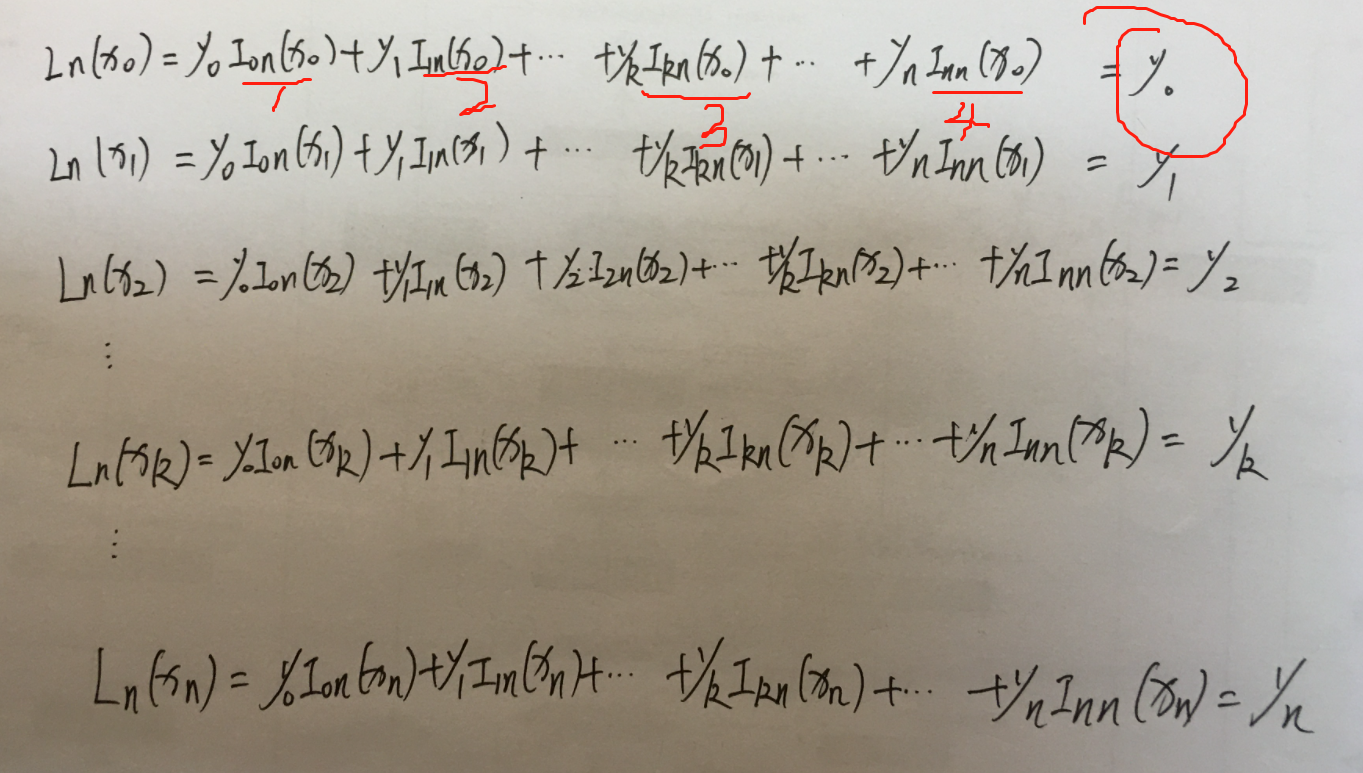
y0与1、2、3、4项无关,那就说明,1、2、3、4项要么为0,要么为1.
假如x*是函数f(x)的一个根,那么一定有(f(x)一定能写成这样的形式:):
f(x)=(x-x*)g(x) ,其中,g(x)的幂数≥0.


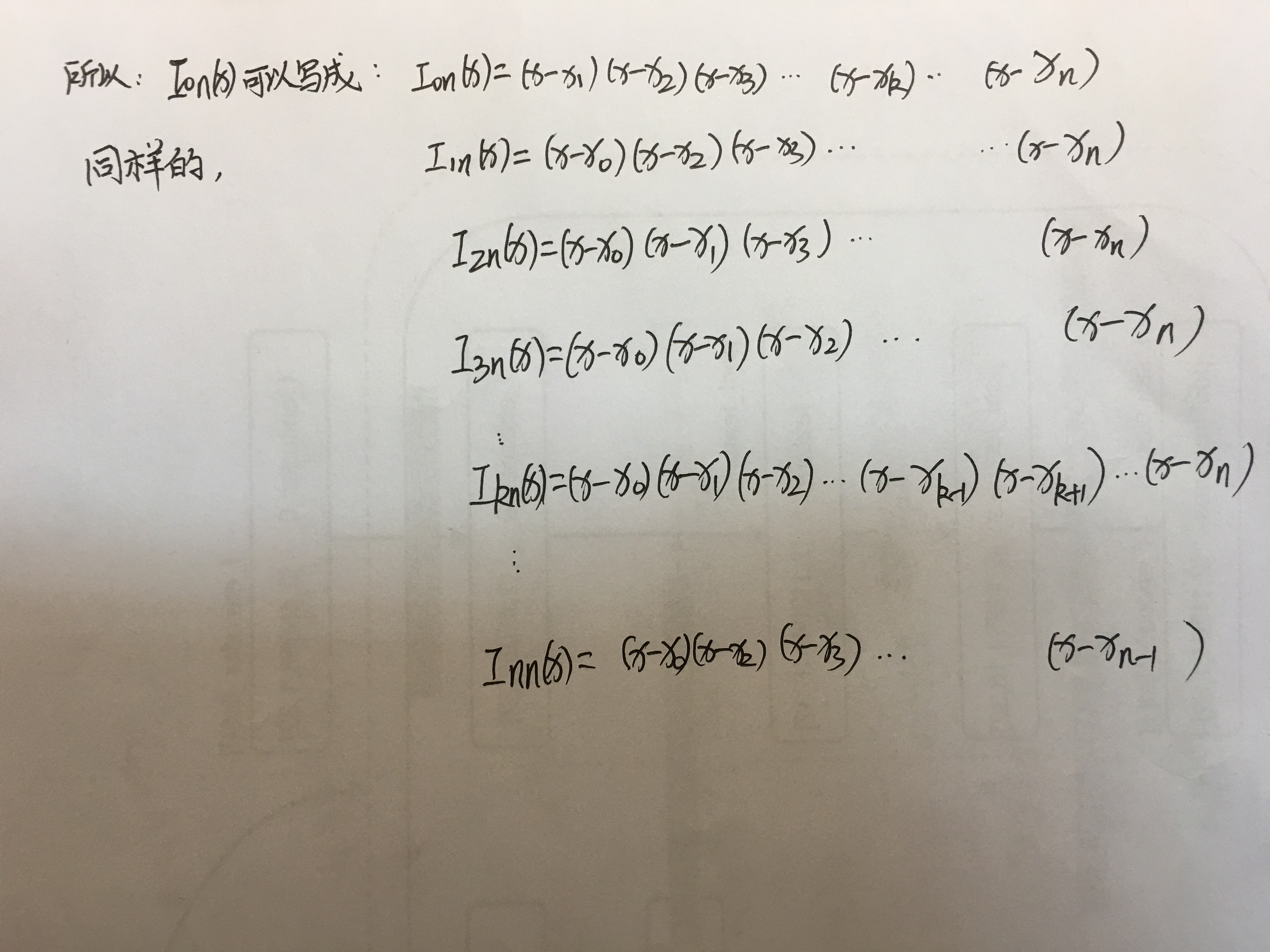

其它的n次多项式也是一样,也可以这样带入这个额外的条件求出来。





既然求出来了,那就说明插值函数是存在的。他越过了线性方程组的求解,避免了面对病态方程求解的困难局面。
下面具体说明拉格朗日插值的写法:




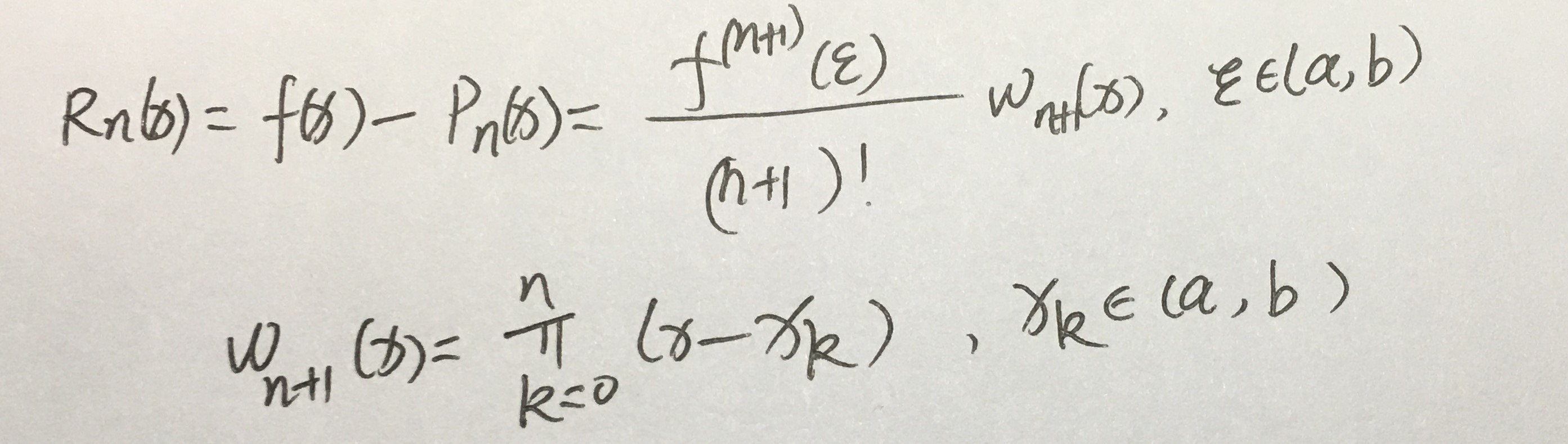
注解:
1.黄色部分是插值余项多项式,通过这个多项式,能知道插值的误差。
2.这个余项表达式是要记住的。
3.在求拉格朗日插值余项的时候,要求被插函数具有直到n+1阶的导数。

注解:
1.在插值点上,余项=0。所以,所有的插值点都是余项多项式的零点。
2.辅助函数在这里特别的重要,它的结构就是:辅助函数(t)=被插函数(t)-插值函数(t)-余项多项式的表达式。

注解:
1.改正:插值多项式P(x)的次数是n次,不是n+1次。
2.x为何也是g(t)的零点呢?
答:因为带入x后:
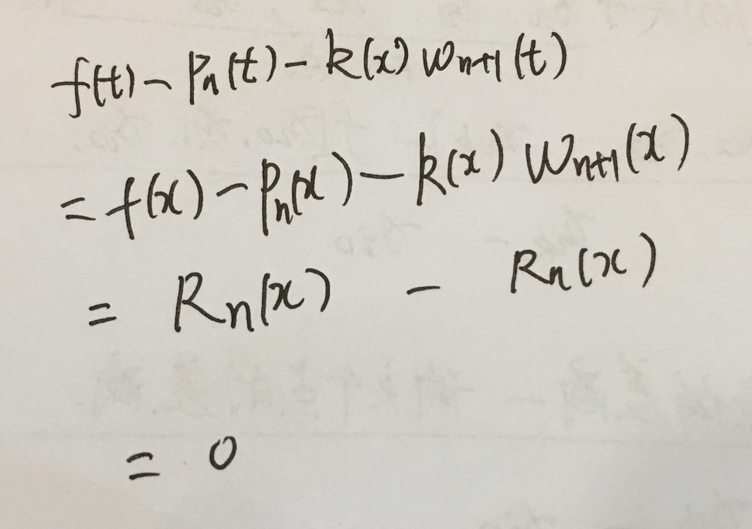

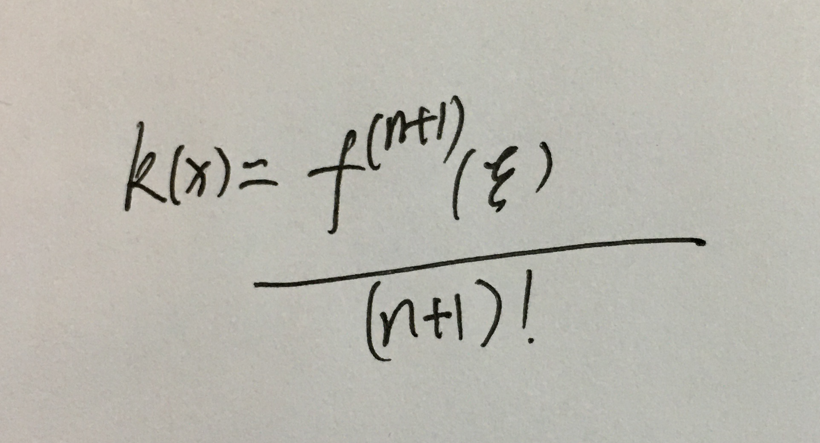
证明过程的关键点是:
1.把余项写成一定的函数结构。根据是余项的表达式中的零点。总之就是,通过找余项的零点把余项写成一定的函数结构
2.做一个新的辅助函数------>构造辅助函数。
3.对辅助函数两边同时求n+1阶的导数,看看余项的n+1阶的导数是不是有一个零点。
4.假定对于辅助函数只找到了[a, b]上的n+1个零点,没有找到n+2个零点,此时对(4.9)式的两边只能求n阶倒数。

5.升维的辅助函数带来的思考:
把等式左边的函数由1个变量写成2个变量:


注:
1.f(x)是被插函数。

注解:
1.式4.11跟x已经没关系了。等式右侧都是数值,这样可以评判出这两个函数最大差是多少,相当于评判出插值函数的好坏。
2.以上是关于插值函数的误差的处理。

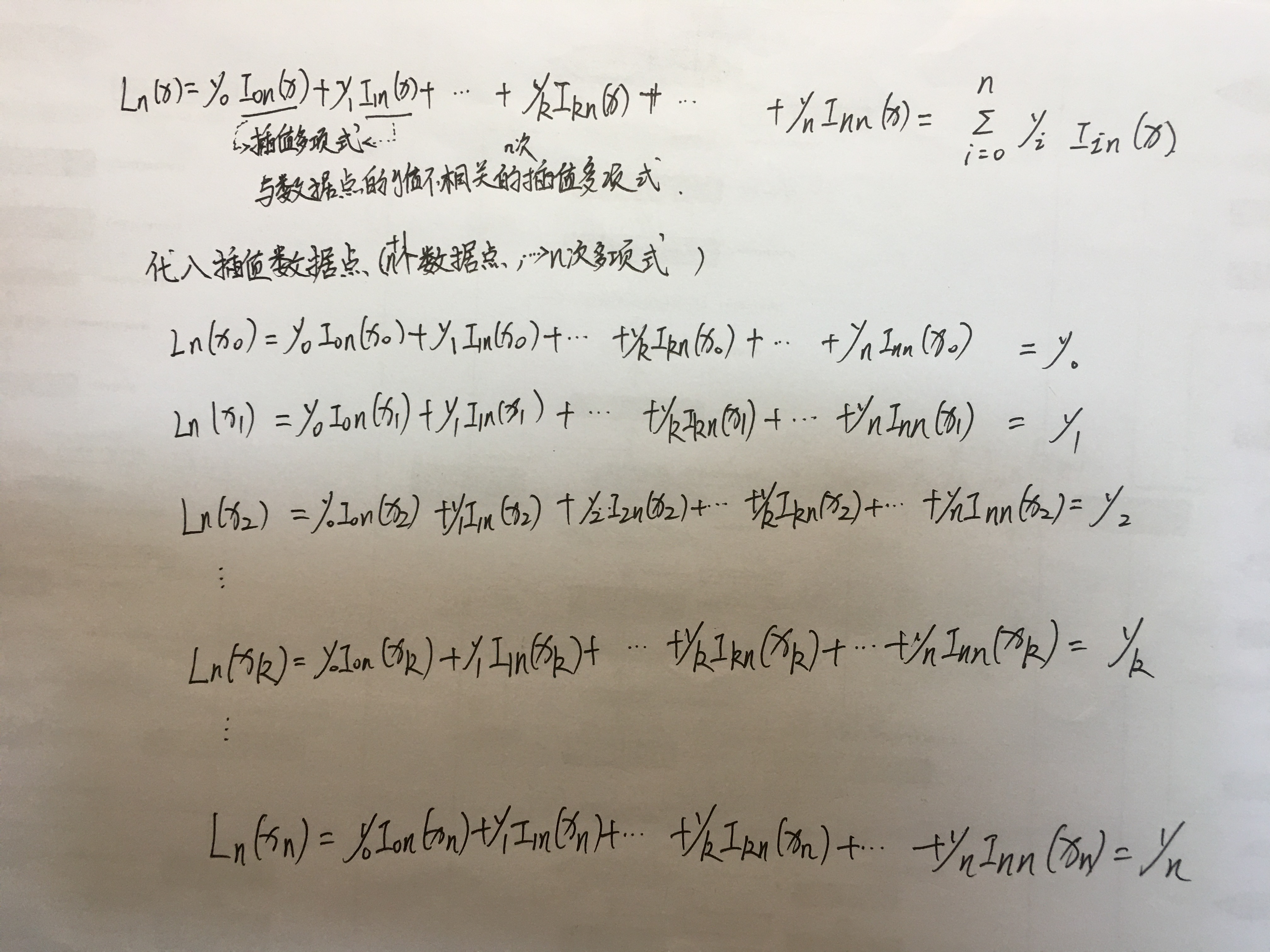


总纲:
插值与拟合问题,它们的本质都是一种数据逼近。


对于拉格朗日插值:
1.先学习他的思想,即处理问题的方法。
插值的次数越高,效果越是不好。
线性插值和抛物线插值的概念:

注解:
1.黄色高亮部分的式子是函数的一种展开式(插值函数+一个余项),是要记住的。

题目讲解:




注解:
1.抛物线插值的时候,要选择3个点,那就选择距离插值点最近的3个点。
这个题目的疑问:既然函数关系知道了,为何还要找插值函数?
答:因为这个函数是超越函数,假如经常重复的计算某个点的值,计算机运行的可能会比较慢,假如是插值,那运行的会很快。
线性插值,只有1个计算量。抛物线插值,也只有2个计算量。
所以,一些复杂的函数,往往用一些简单的插值函数来代替它。
插值函数第一个重要的作用:用于函数计算。知道函数在某些点的值,但还想知道函数在其它地方的值。
注解:
1.线性插值,给了5个点,用2个点就行了,插值一个1次多项式。
2.抛物线插值,给了5个点,用3个点就行了,插值一个2次多项式。
3.越近的点影响是越大的,越远的点影响越小。这是因为越近的点,分母的值越小,越远的点,分母的值越大。

二次插值计算误差项的时候,少一个因子,正确的应该是:


注解:
1.同一个位置,可以看到,2次插值的误差比线性插值的误差小很多,一个是-5次幂的数量级,一个是-3次幂的数量级。说明:高次插值比低次插值误差小。在形式上看,余项的那个分母中有个阶乘项,插值的次数(阶数)越高,那个阶乘越大,余项的值就会越小(理论上是这样)。





注解:
1.步长大了如何,小了又如何呢?
答:步长取的太大的话,当前点的误差小,但是当前点旁边的点误差会比较大。步长小的话,插值点会比较密集,各个地方的点的误差会比较小。
2.既想用二次函数来代替这个函数,又想截断误差小。
3.插值方法可以应用到找油田的应用中。
4.等距的意思: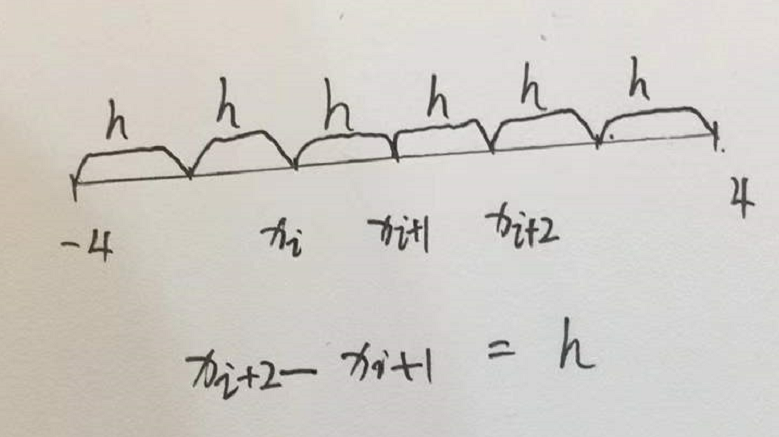
4.随着i的移动,点会遍历到整个[-4,4]区间。
5.对于x=xi+th(t∈[0,2])的解释:
当t=0的时候,x=xi,当t=2的时候,x=xi+2,右边的区间端点。当t在[0,2]之间的时候,x会遍历[xi,xi+2h]这个区间。


注解:
1.有了插值节点了,那怎样构造插值表呢?
答:对于当前的节点,利用左右相邻的2个节点,调用二次插值多项式,进行插值,算出当前插值点的值。
应该不是这样理解的,问题里面插值表应该是已知的,在插值表已知的情况下,要求插值后的阶段误差小于某一个值。
重点:
1.有n+1个插值点,如果被插函数是个次数≤n次的多项式,那么(拉格朗日)插值多项式可以100%把被插的多项式还原出来。

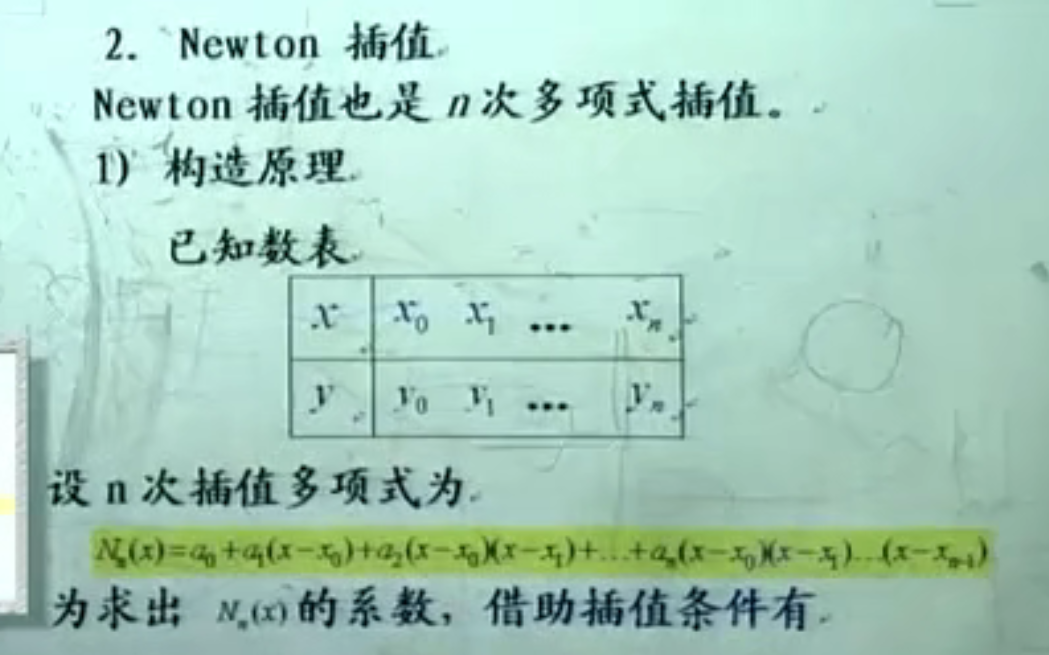
注解:
1.牛顿插值,还是多项式插值,还是相当于是越过了求线性方程组的解面对病态方程的困难。
2.每次的因子都多一个因子。
3.把求插值多项式的问题还是归为求系数的问题,拉格朗日是归为求基函数的问题。

改正:

4.牛顿为何能想到以这样的形式做?

5.系数ai存在且能求出来,这样的设计才是有用的。只能通过插值条件进行确定了。
6.当把x0带进去的时候,从第二项开始全部是0,这样a0可以解出来。
当把x1带进去的时候,从第三项开始都是0了,这样的话a1可以解出来。
。。。
7.牛顿不但利用这种方法解决了插值多项式的问题,而且得到了一个新的理论:差商理论。




注解:
1.2个点----1阶差商。

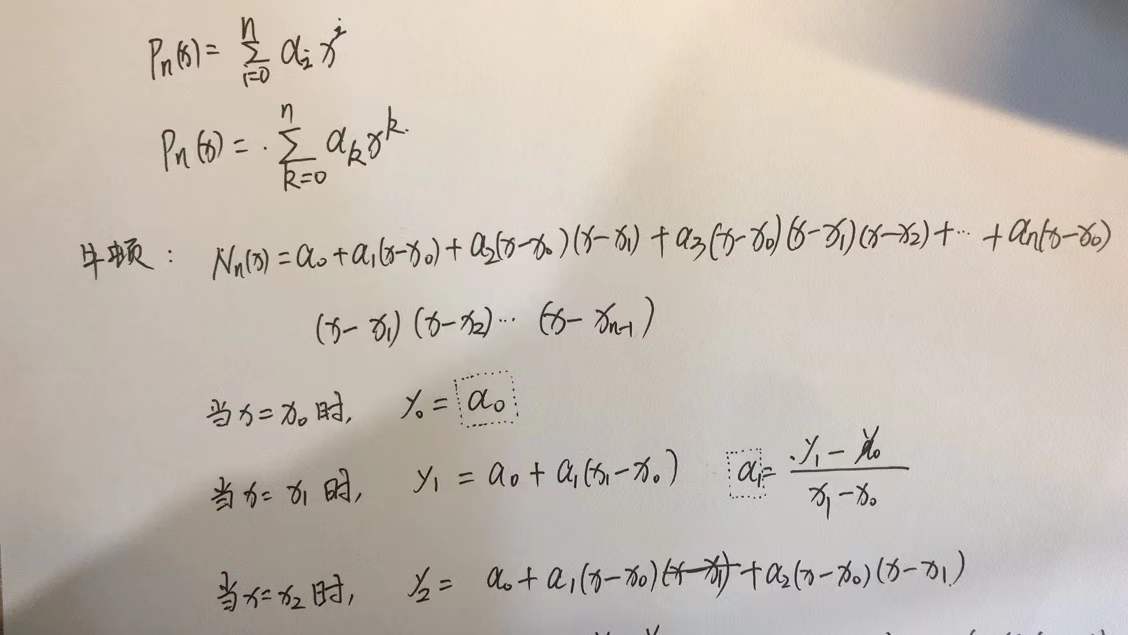
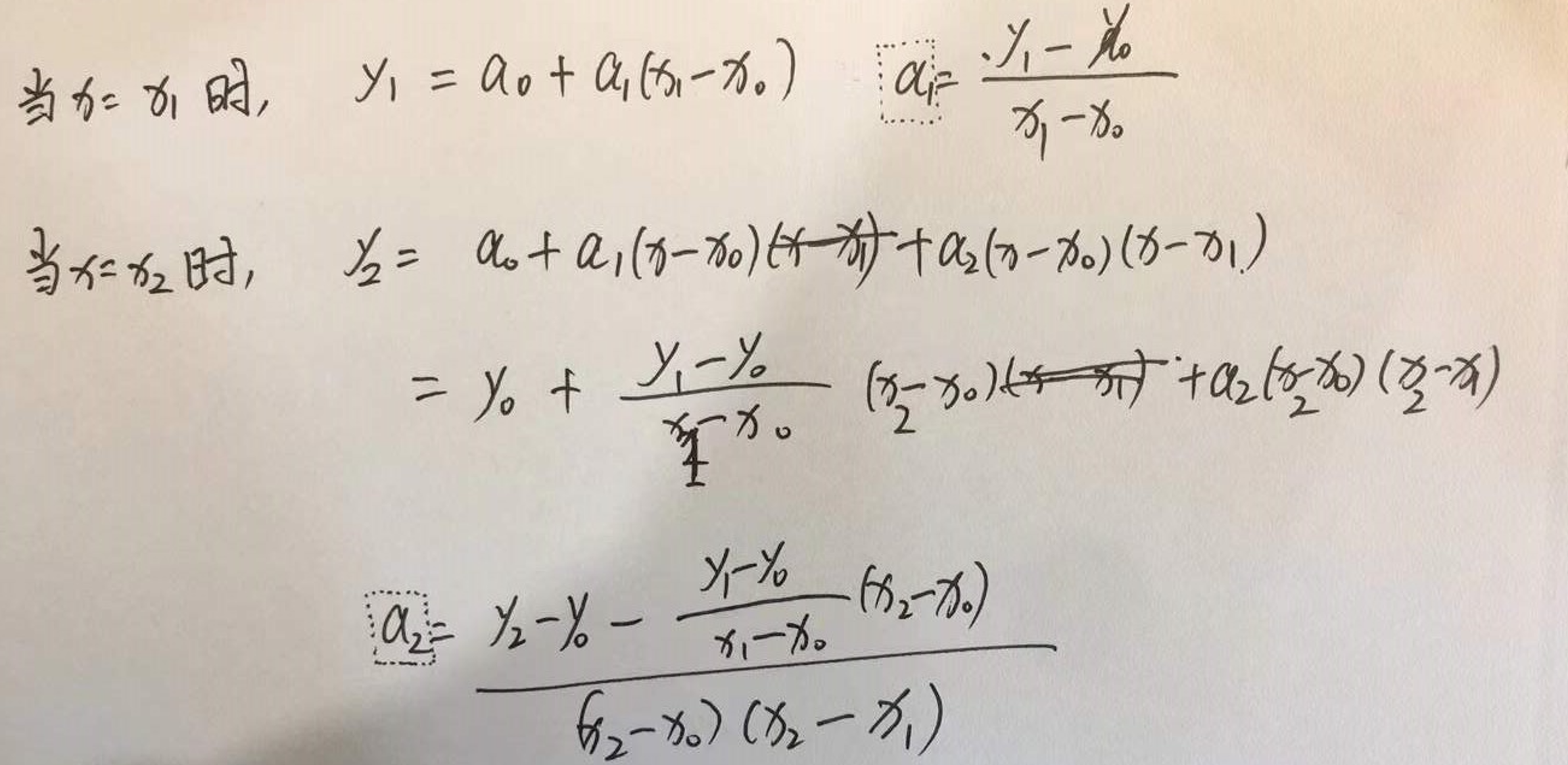

下面这个是一阶差商:
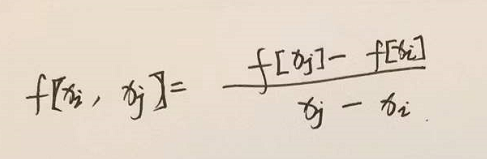

注解:
1.不要求求导数,涉及到求导问题的时候,函数不可导的时候,差商都可以做的。
2.根据1,相对于拉格朗日插值,不要求被插函数有n+1阶导数了,
3.牛顿插值里面的系数正好就等于差商。从下面的a0,a1,a2就能看出来了。

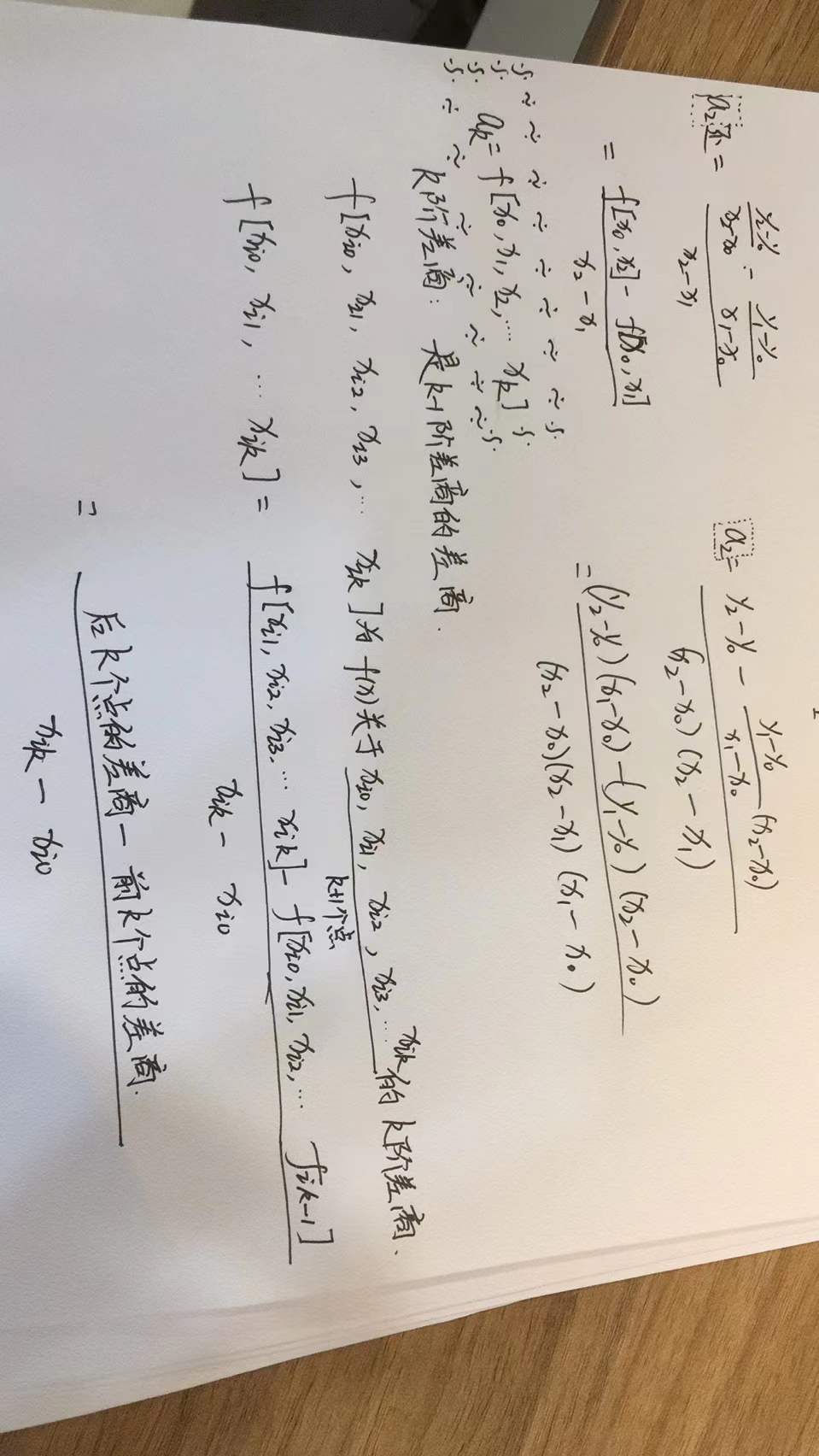
注解:
1.ak=f(x0,x1,...xk) k的取值是1,2,...n

注解:
1.差商表看上去像是一个左上三角矩阵。
2.每一个差商都是:(左侧相同行的值-左侧下一行的值)/自变量相减。
例如:
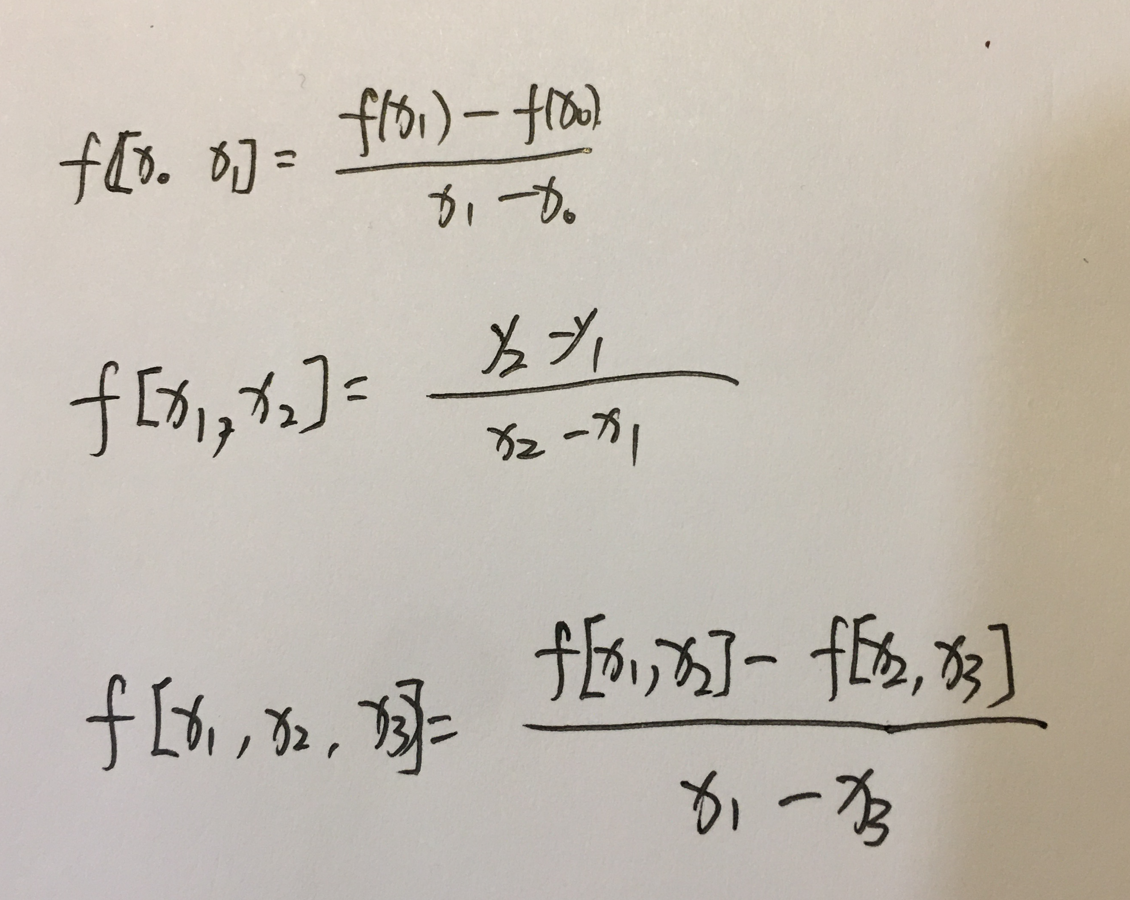
3.差商表结构比较清晰,编程也会很方便的。






注解:
1.当t=x的时候,即t在x这一点上,Nn+1(x)=f(x).等式的左边是插值函数,等式的右边是被插函数。
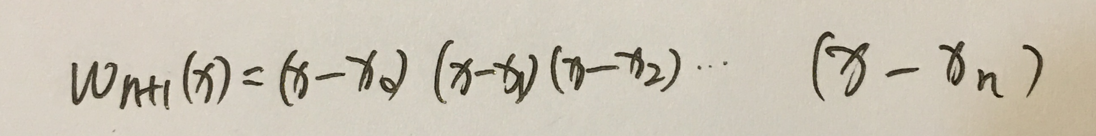

注解:
1.因为插值函数具有唯一性。所以,




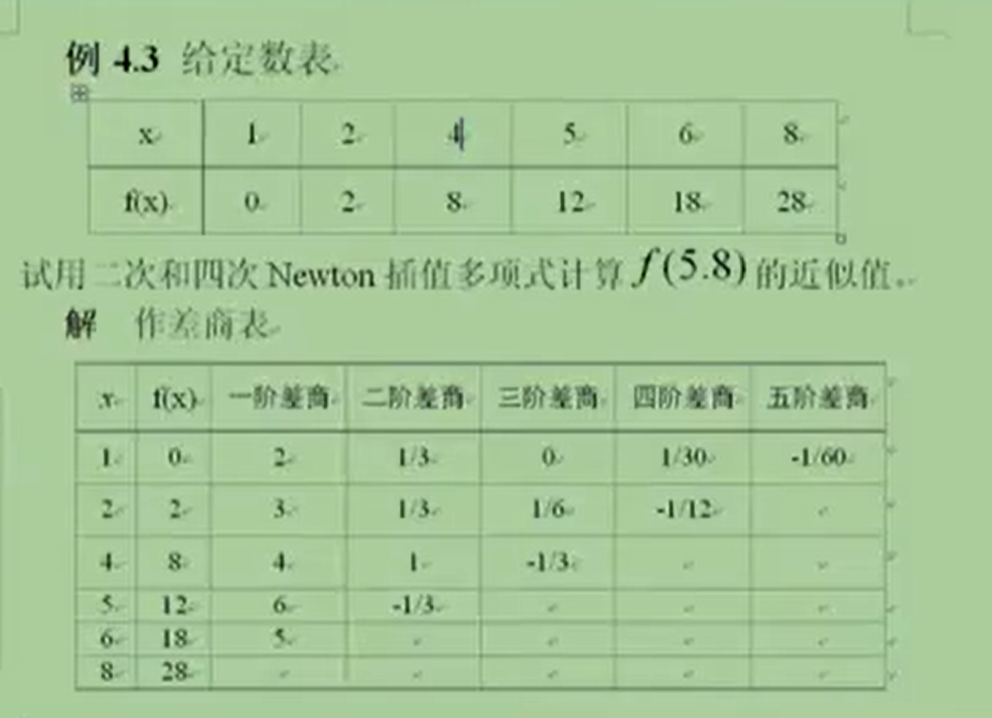





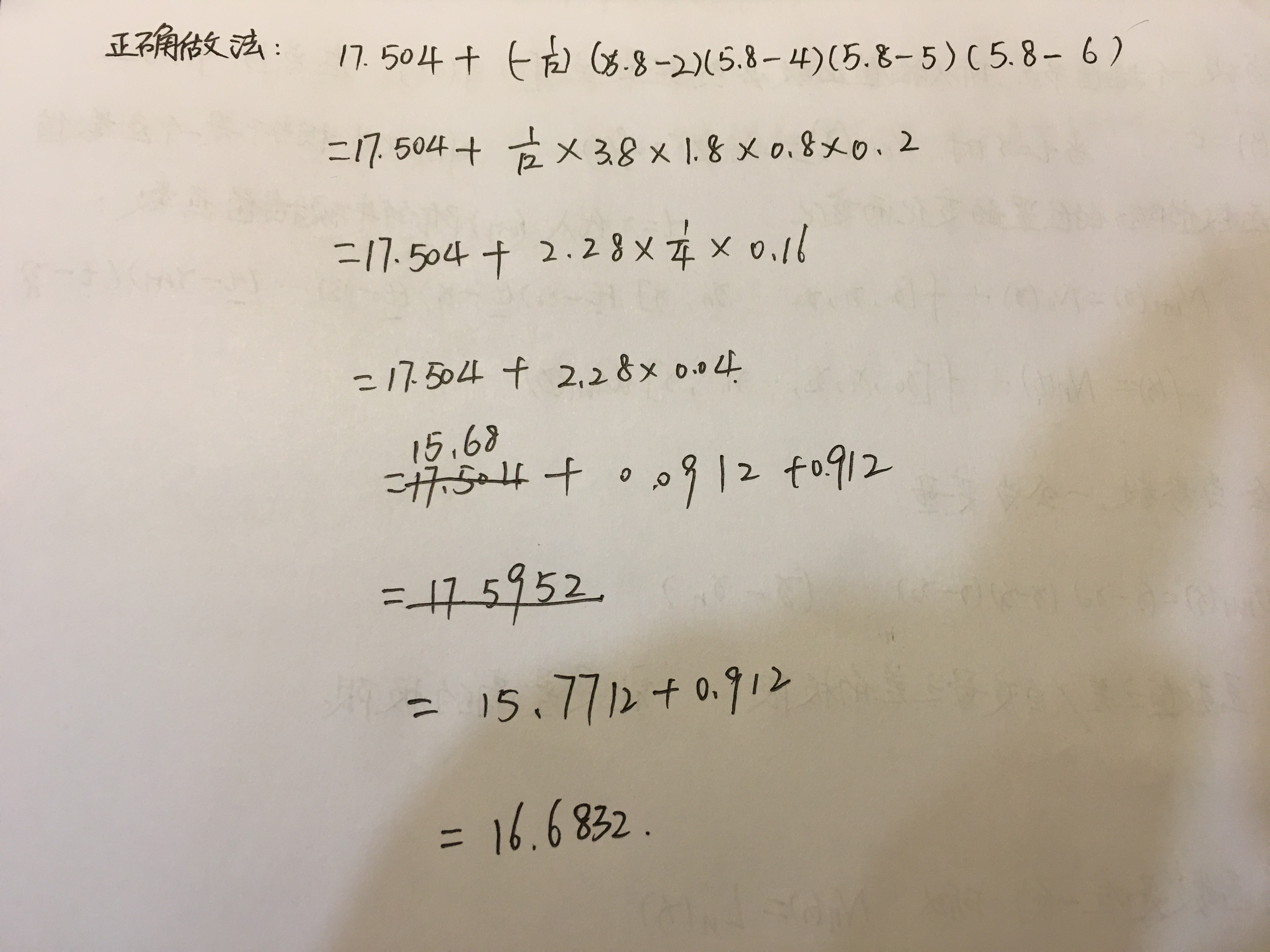
注解:
1.有了差商表,我可以做任何幂次的插值多项式。

牛顿插值的知识点到此结束。


插值:给出一些未知函数或者已知函数上的信息(如一些点上的函数值,导数值),找到一个近似函数,至少在这些已知信息上,插值函数和被插函数是相同的,这就叫做插值。
Hemite插值:加入导数信息的插值。


解决思想:往拉格朗日插值的方法上靠。
注解:
1.给了被插函数(未知或者已知)的n个信息,可以确定n-1个系数。
2.本题目给了4个已知信息,假如用多项式来做的话,可以列4个方程,解4个系数,确定一个3次多项式。
3.在知道了已知信息后,拉格朗日是怎么做的?
答:把插值点上的函数信息(函数值或者导数值)乘上相应的基函数,然后相加。导数值也是函数信息。接下来的事情就是求式子里面的4个函数了。
4.在插值点上,插值函数和被查函数的值是相等的,那么在插值点上,基于插值函数和被插函数的相似性,它们的导数也应该相等的。

注解:
1.为何在第一个插值点上,α1(1)=1,α2(1)=0,α3(1)=0,α4(1)=0,这是因为假如后三者不为0的话,那么H(1)=f(1)=0就不成立了。
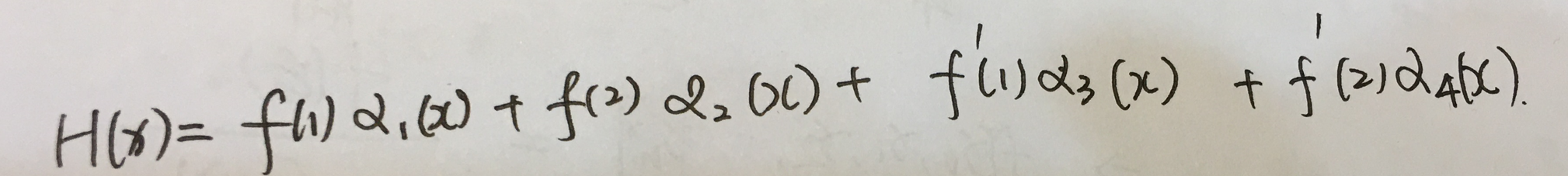
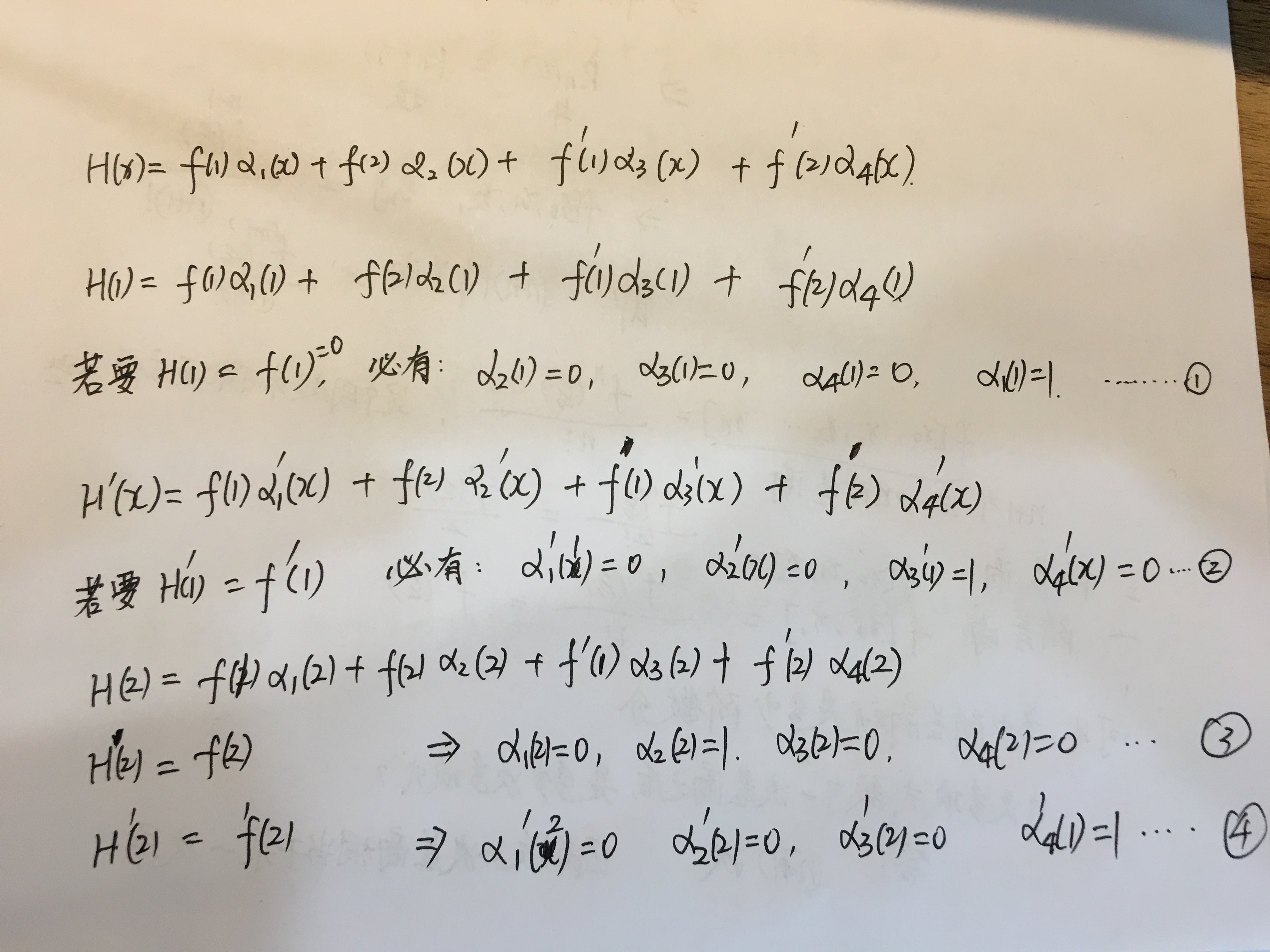
注解:
1.拉个朗日插值的一个重点是:构造插值基函数的结构。
![]()
2.
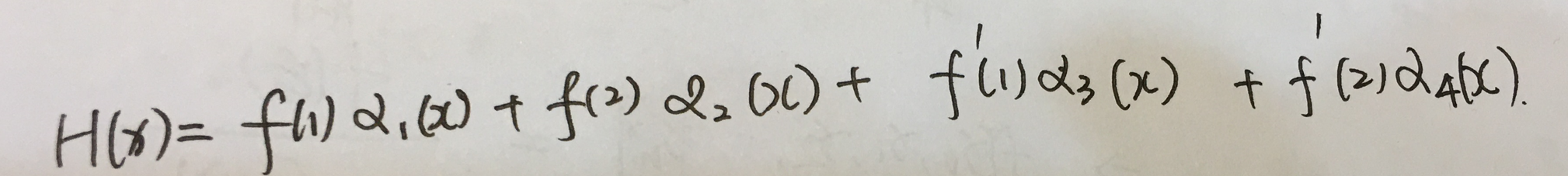
中的α(x)就是插值基函数。
3.要弄清楚基函数中的0因子。
如果一个函数f(x)有0点x*,那么函数一定能写成: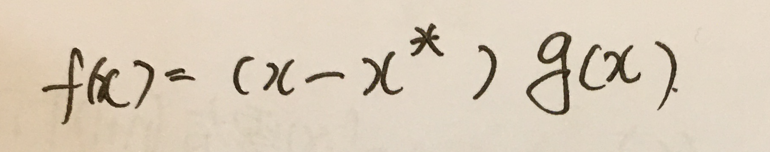
4.如果:
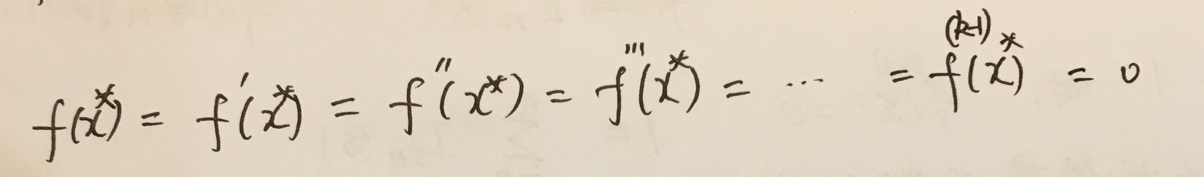
那么f(x)一定能写成:
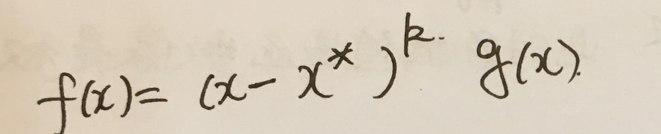
如果:
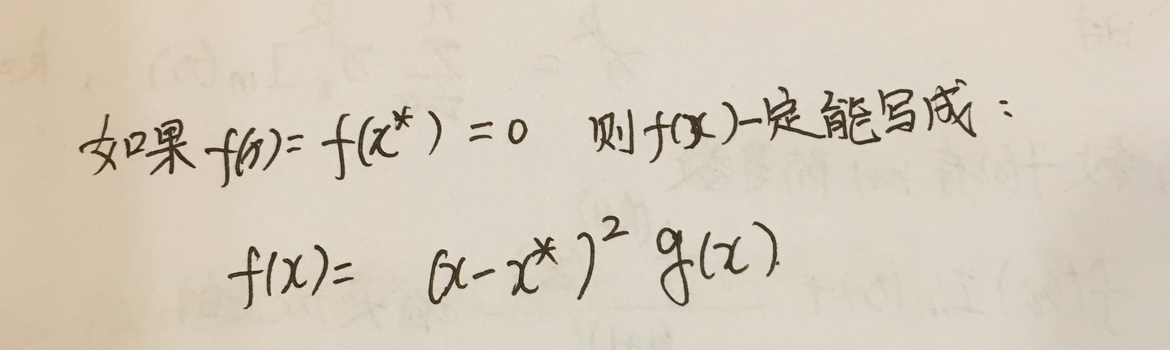
5.在考虑α1(x)的结构的时候,要先找它的零点。


注解:
1.解的过程还是拉格朗日的东西。
2.余项就是被插函数和插值函数做差,拉格朗日是先把余项的结构弄出来。弄函数的结构就相当于是找函数的零因子。
3.在插值点上,由于插值函数过插值点,所以插值点上余项是0,但是在插值点上余项的导数也为0,这是为何呢?
答:在插值点上,被插函数和插值函数的导数值也应该是相等的。


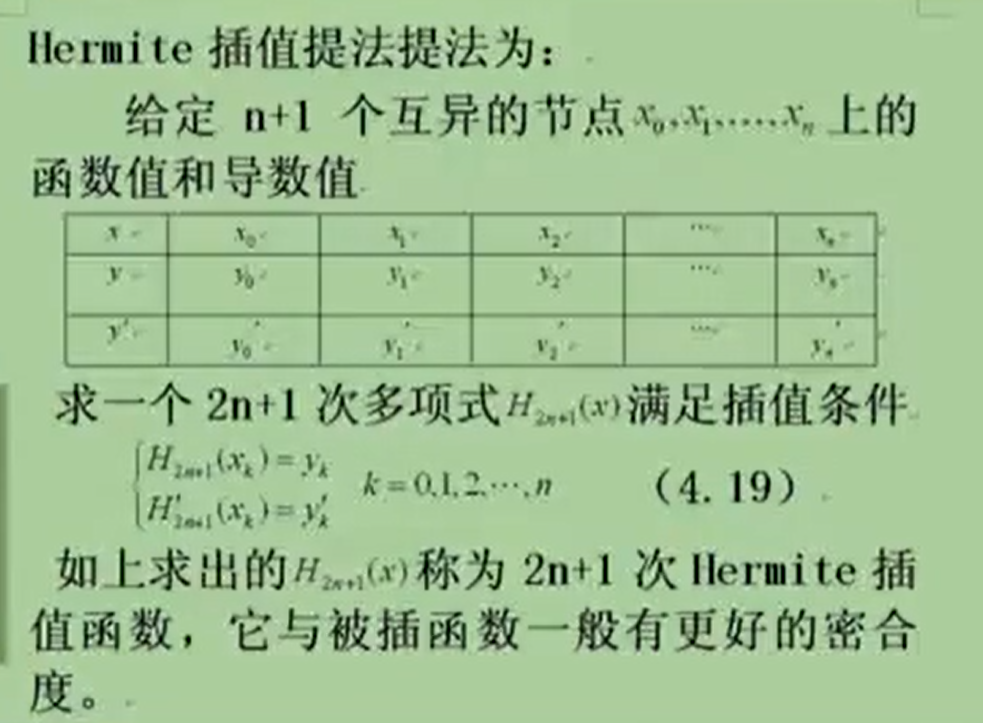
注解;
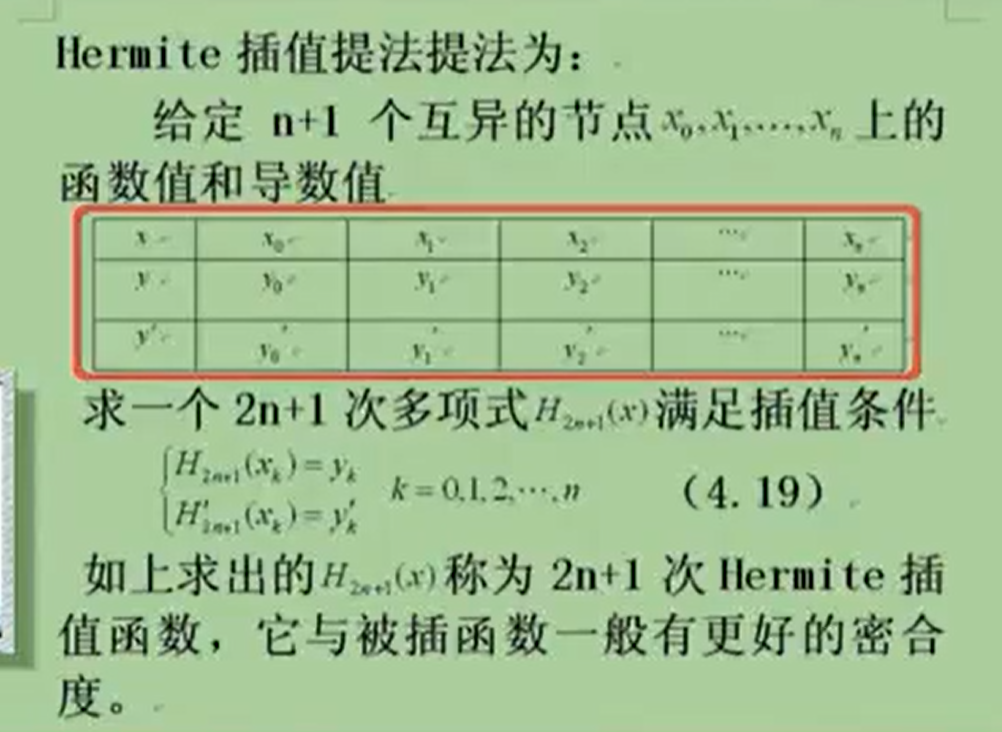
1.给出的条件是2n+2个已知条件,所以可以插值出一个2n+1次的多项式。


注解:
1.带有导数信息的插值都可以称为Hermite插值,但这个问题不是标准的赫尔米特插值,因为知道的已知信息不是插值点和对应的导数值。

[Class]数值分析.王兵团.北京交通大学.全128讲[48:35:32]_哔哩哔哩_bilibili
注解:
1.求插值函数的思路:让插值函数和被插函数在已知信息上(如函数值和导数值)相等。
2.指数插值,三角插值也都是可以的,但是它们做起来比较麻烦,都没有多项式插值来的简单。
3.一个等式就是一个插值条件,条件也可以称为约束。
4.插值多项式的次数始终是:条件数量-1,因为多项式有个常数项。
5.为何Hermiter插值函数有更好的蜜合?
答:因为插值函数和被插函数不但插值点上的函数值相等,而且导数值也相等。导数值相等就相当于是插值点附近的函数走向也基本上一致。假如只是在插值点处的函数值相等,那插值函数也可能是下面这样尖尖的,假如要求导数值也相等的话,那插值函数就必须是平滑的了,也就是和被插函数应该会更蜜合的了。
- 下面是Hermite插值的推导。
第一步:仿照拉格朗日插值多项式的构造,首先设置插值函数的形式:
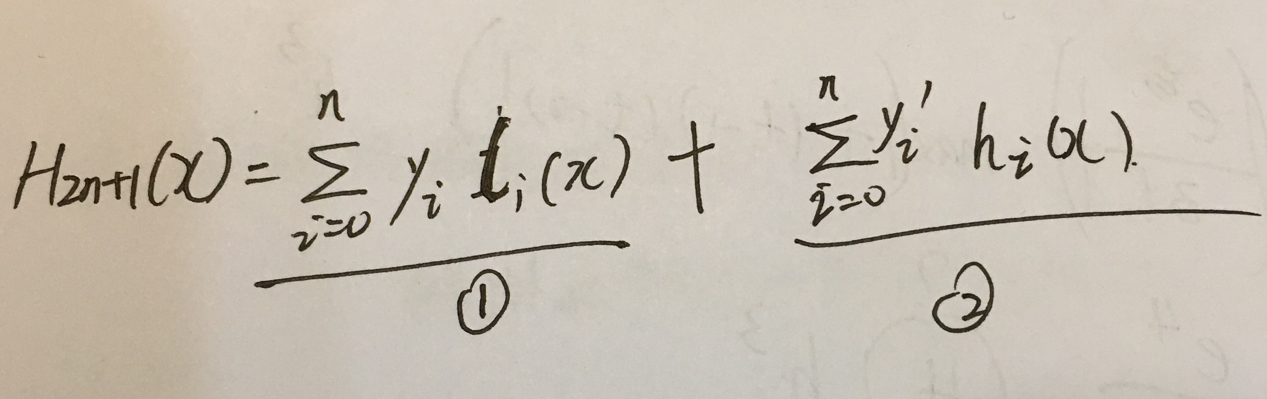
注解:
1.第1部分是拉格朗日插值的部分,第2部分是加上的导数部分。
2.总是利用一些已知的函数值信息乘以一个未知的函数,然后进行代数和相加,来做插值函数的形式。
3.无论是第1部分里面多项式,还是第2部分里面多项式,它们都是2n+1次多项式。
第二步:
根据插值条件写关系式,求出插值基函数。·
一般做的话都是做两个点的,简单一点。相当于是2个点,4个条件,做一个3次插值多项式。
第三步:
写余项。
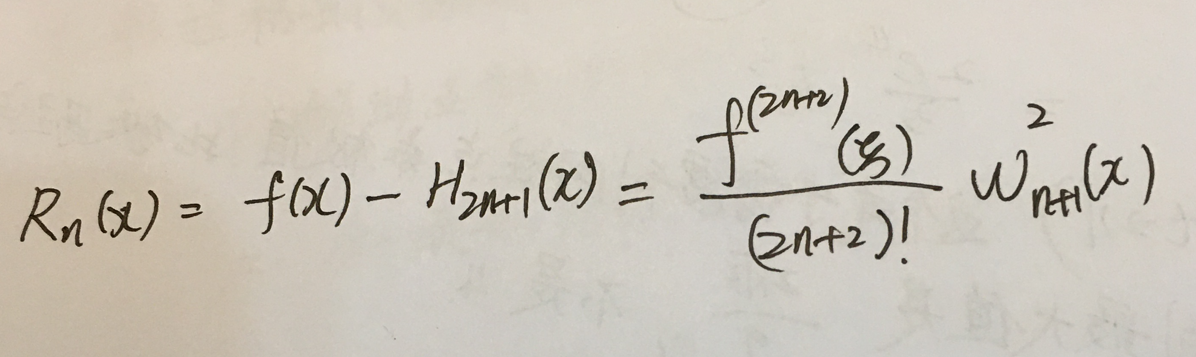


注解:
1.插值条件的个数也可以说成是插值信息的个数。

注解:
1.知道的信息:
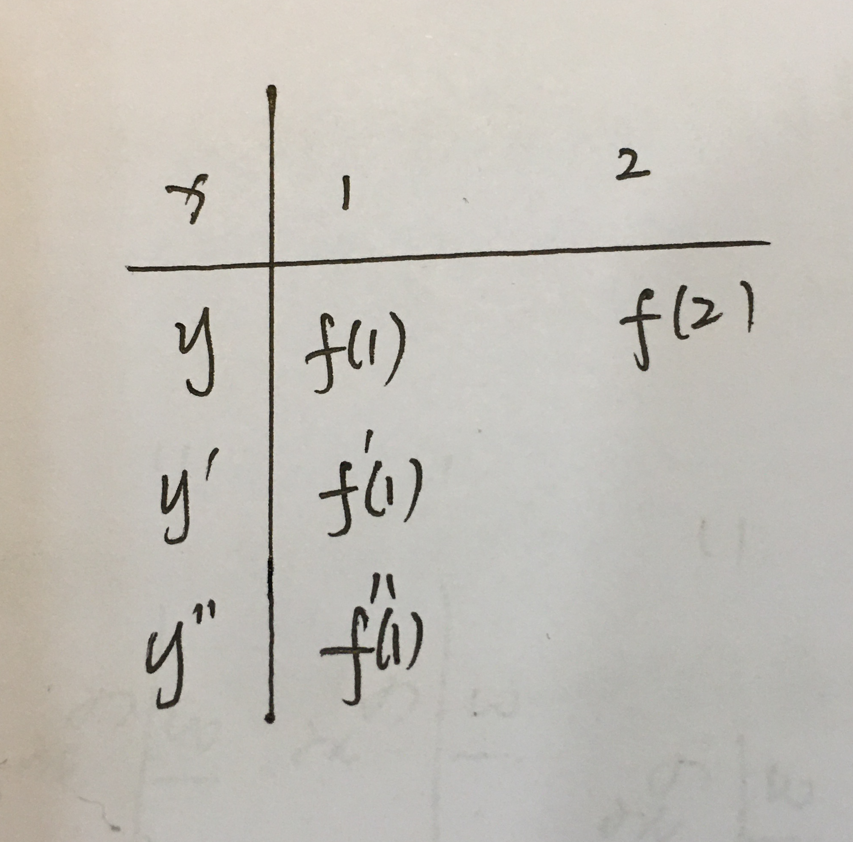
2.确定插值多项式次数和结构。
次数:4个条件-->3次多项式。
插值多项式结构:所有的函数信息(函数值)乘上待定函数(基函数-->3次多项式)。
这一步不像是Hermite的做法,这里是拉格朗日的做法。
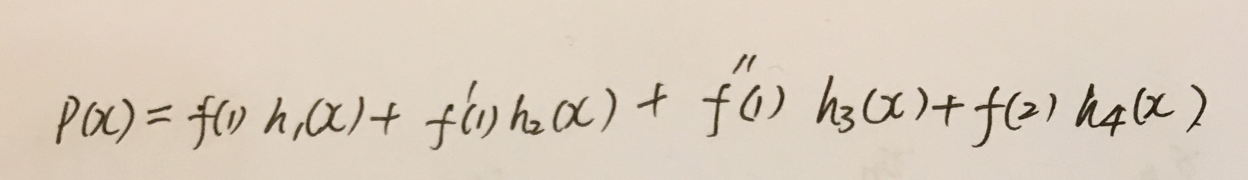
3.在插值多项式中带入插值条件。
规律:其中一个基函数等于1,其他基函数等于0.
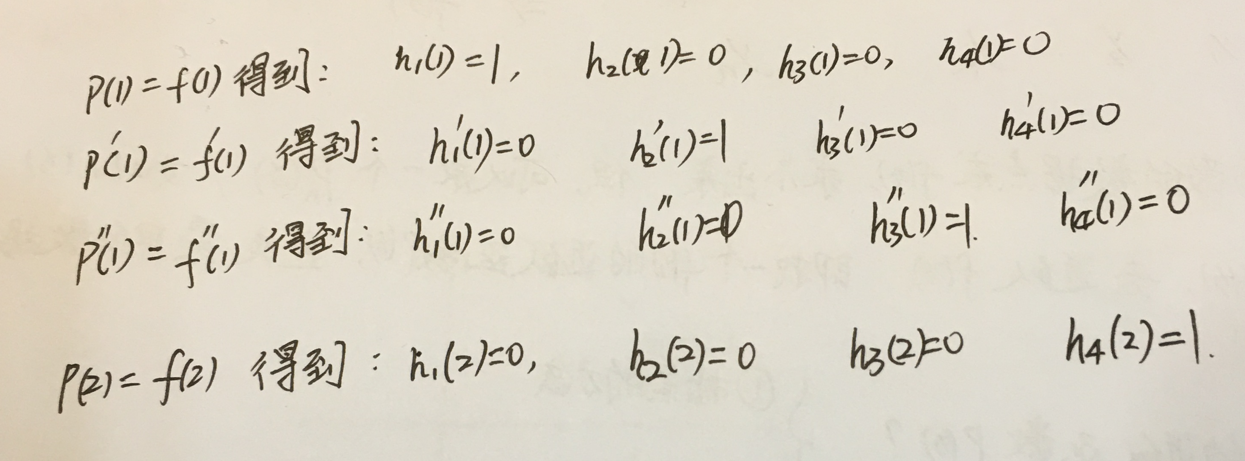
4.利用h1(x), h2(x), h3(x), h4(x), 都是3次多项式,写出它们的形式,然后根据第3点中它们的零点和非零点条件求出系数。

基函数h1(x)的形式的考虑:


注解:要是不那样设基函数h1(x),结局一定是利用前3个条件解一个线性方程组,比较麻烦。
基函数h2(x),h3(x),h4(x)的形式的考虑:


考察误差:

注解:只说让写出误差表达式,没说让证明。
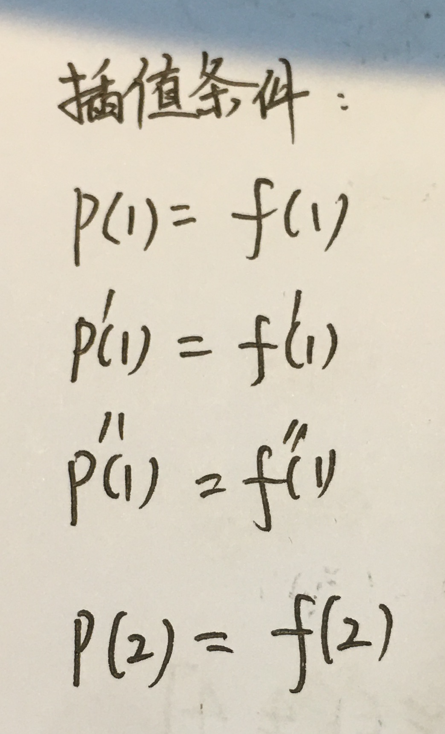
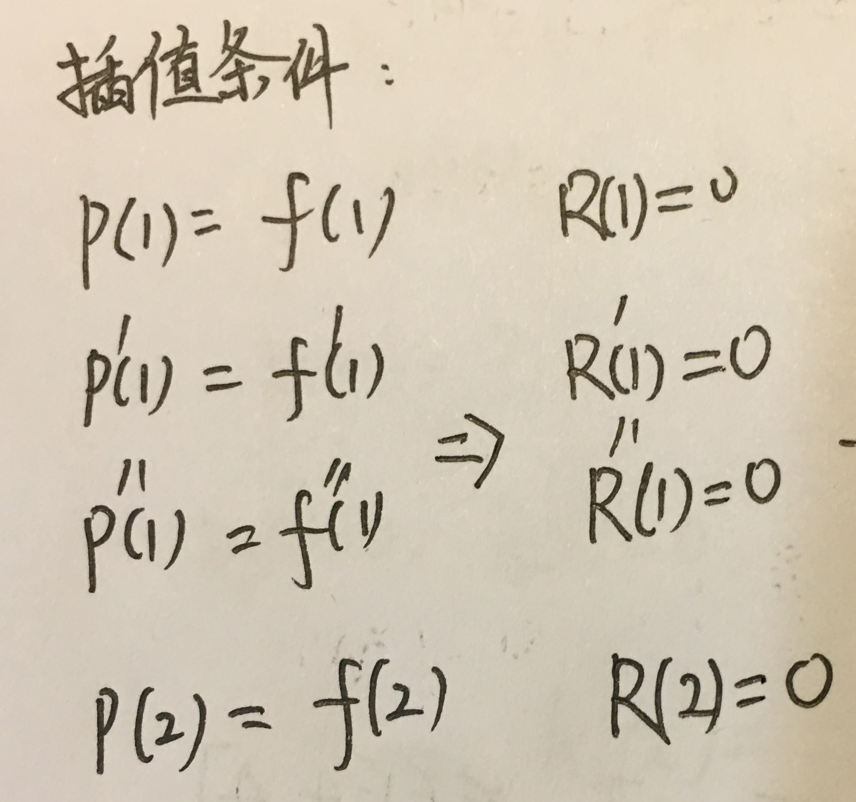
注解:其实R(x)不知道是多少次幂的多项式。
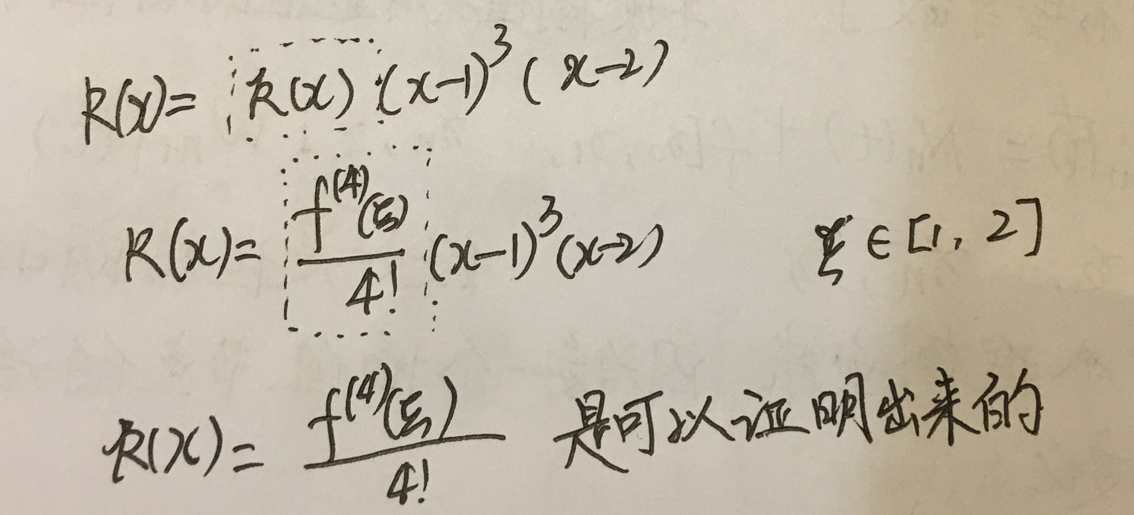
k(x)=?是可以直接看出来的:分母是信息个数(4)的阶乘,分子是信息个数(4)阶的导数。
怎么证明?
答:仿照拉格朗日余项的式子的证明给证明出来。
证明如下:

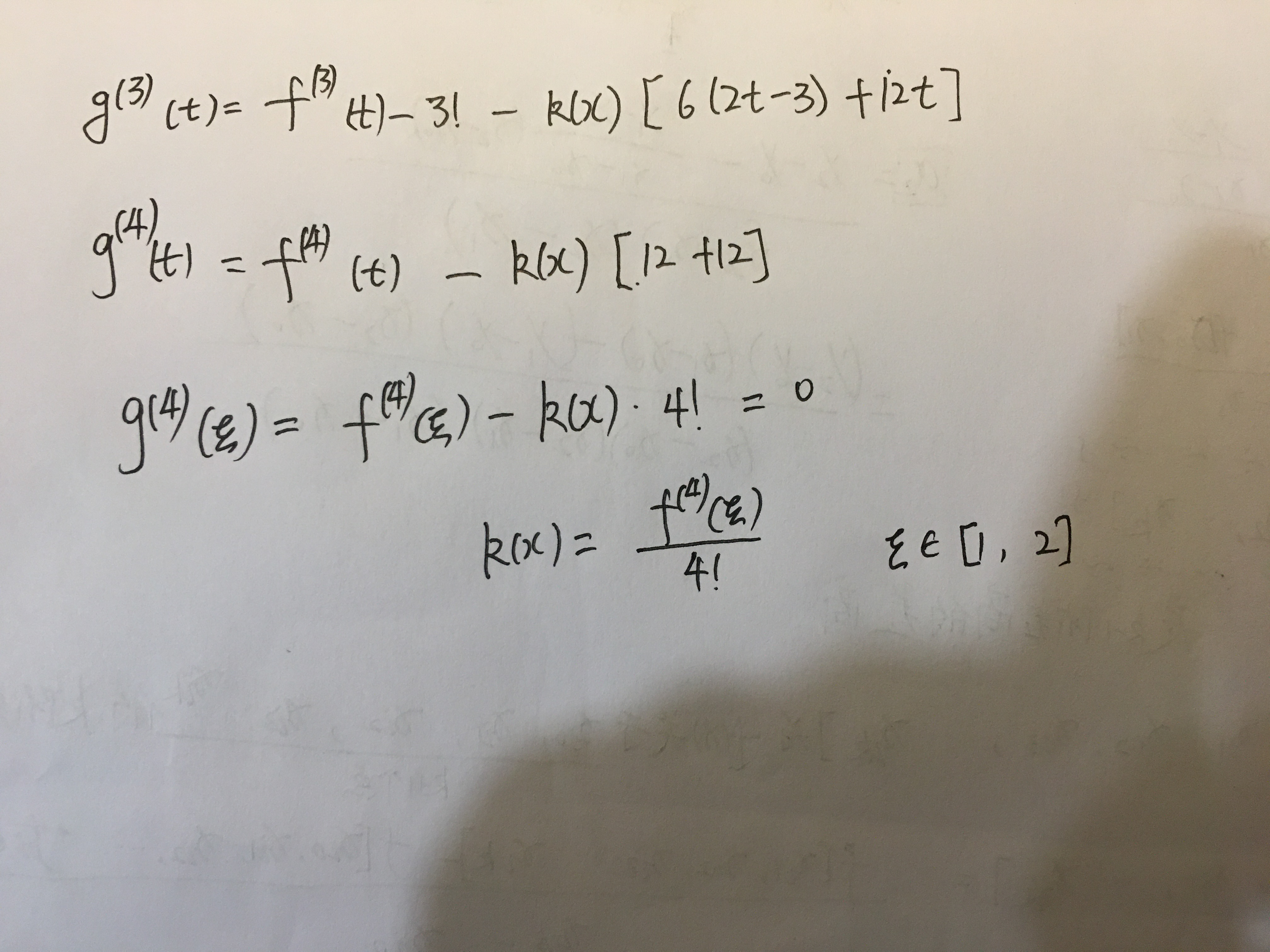
注解:
1.Hermiter插值的余项,不像拉格朗日插值的余项那样,在求零点的时候,只有函数值上有零点,Hermiter插值的余项,除了函数值上有零点外,本身的导数值也有零点。
考察拉格朗日插值的余项,既然插值余项的分母中有一个阶乘项:
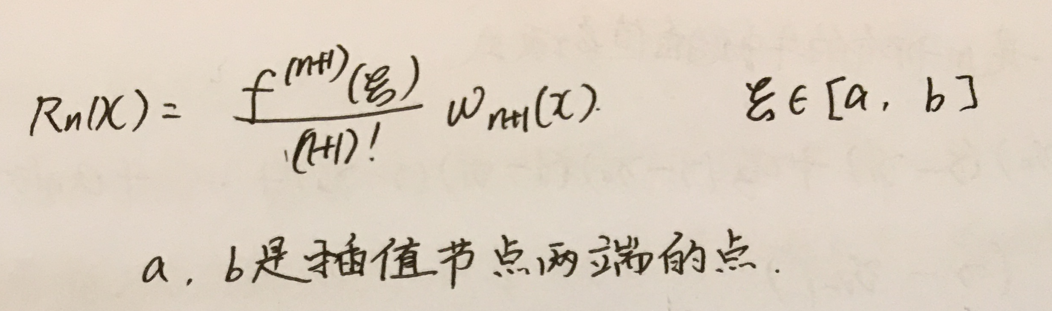

那是不是插值点数越多,插值的次数越高,误差就越小呢?当插值的次数n趋近于无穷大的时候,误差余项就趋近于0(阶乘是很大的),插值函数P(x)就无线接近于被插函数f(x)了,是这样吗?
答:不是,插值次数过高的时候,会出现隆格现象。

这会造成一个错误的印象:只要用更多的插值节点,提高插值次数,那插值函数的误差就会无限小。二次插值比线性插值的精度高,三次插值比二次插值的精度又高,实际是,插值次数很大的时候,插值误差不但没有减小,而且还增大了。就是说插值次数很大的时候,精度不但没有提高,而且还降低了。这就是龙格现象。
谁这样做了呢?
答:Runge.


n=2对应:3个插值点
n=6对应:7个插值点
n=10对应:11个插值点
n=14对应:15个插值点
n=18对应:19个插值点
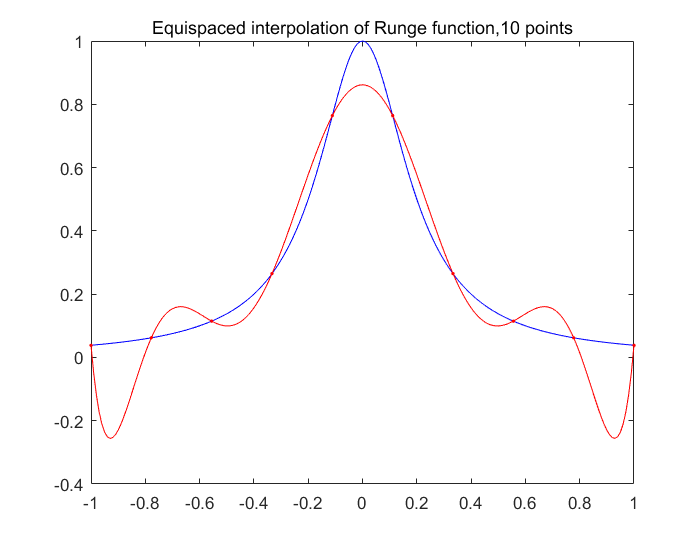
龙格现象的参考链接:
龙格现象(Runge Phenomenon) - 知乎 (zhihu.com)
数值计算(三十六)Lagrange插值的Runge现象 - 知乎 (zhihu.com)
龙格现象主要出现在插值函数的两端,中间部分会好一些。
给定一个已知函数,取上面的一些点进行插值实验,随着采集的实验点的增多,插值多项式的次数一定是逐渐增高的。
一次插值:不拐弯。
二次插值:拐一个弯。
三次插值:拐二个弯。
一般认为,随着次数的增高,函数图像摆动的弯也是增多的。高次插值的情况:插值函数一定要过很多点(某种程度上来说,插值点固定了函数的走向),要拐很多弯,所以在过点时候,拐的弯过大的话,拐弯地方的误差就会很大了。
另一方面,计算机做的时候,又有舍入误差。
一般来说,
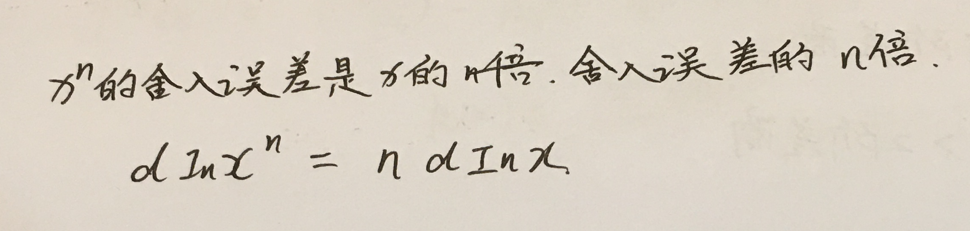
怎么解决龙格现象呢?
答:因为给的点数多,会造成高次插值出现龙格现象,即误差变大的迹象,为此,人们提出了把插值点分段,进行分段多项式插值的概念。

分段插值,就是一段一段的进行插值(分段低次插值),这样每一段的插值点个数就有有限了,从而限制插值多项式的次数。

似函数。

注解:
1.第1点是在整个插值区间上,插值多项还是连续的,不能间断。近似函数都有这个要求的。
2.第2点是满足插值条件。
3.分段函数之所以麻烦,在于不同的段上有不同的表达形式。
4.分段m次插值,用的最多的还是分段线性和3次插值,分段2次和分段4次用的很少,为何不用分段2次呢?
答:2次插值的话,函数的凸凹性不好,要么是凸的,要么是凹的。而3次插值就不一样了,函数图像有凸有凹,可调性稍微好一点。还有,2次的偶次的,描述事情的范围窄。而奇次的有时候可以描述偶次的,有时候可以描述奇次的,描述的东西更多。
5.医院里面的心电图很多是用分段线性插值做的。

注解:
1.实际上,把拉格朗日一次线性插值用在每个小区间上,就是分段线性插值了。

分段线性插值的结果,实际上是各个小区间连接起来后的折线,整体折线是连续的,但是在各个小区间端点处,相邻小区间的连接点处的导数值是不相等的,函数图像看起来是很不平滑的。现在想让相邻小区间的连接点处的导数值也相等。

注解:
1.用4个点做分段3次多项式也可以,但是连接点处的密合程度可能不够。假如连接点处的导数值也相等的话,那密合程度会很好,会有很好的蜜合性。
2.上面说的分段线性插值和分段3次多项式插值,分段多项3次多项式插值指的是赫尔米特插值,不是一般意义上的4个点3次的拉格朗日或者牛顿多项式插值。
3.分段3次赫尔米特插值笔分段线性插值的效果要好因为分段线性插值连接点处的函数图像有尖,这样光滑性就不好。如果坐轮船或者飞机的话我们希望轮船的船体或者飞机的机体是光滑的这样阻力就会小。
4.分段3次赫尔米特插值,连接点处导数存在的话就没有尖点了,导数再相等的话那光滑性和密合性就会更好。

注解:
1.分段插值可以实现真正的高次插值而且不会出现龙格现象。如果选择的点数足够多那么插值函数就可以无限的逼近被插函数。


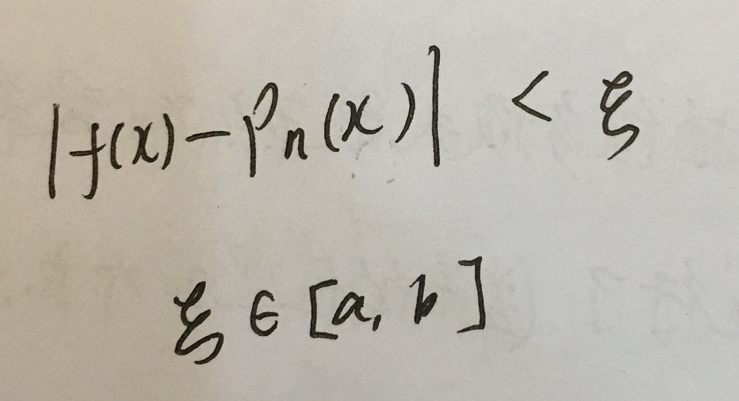
注解:
1.拉格朗日插值不能使误差无限的小假如强行增加插值点增加插值的次数让误差无限的小会出现龙格现象。
2.分段Hermite插值,只要h足够的小就能让误差足够的小。
3.分段子3次赫尔米特插值比分段线性插值的误差更加的小。 h般都是小于1的这样的话它的4次方会比2次方更加的小。
4.分段线性插值如果它的插值的点很近的话,即h足够小的话,那么它的插值图形会变得很平滑。心电图图像就是这样做出来的。
5.所以一般在做近似函数计算的时候,假如选择插值的方法一般会选择赫尔米特插值一般不会选择拉格朗日插值或者牛顿插值,后两者是理论的东西。
下面证明两点3次赫尔米特插值的误差余项,一般是选择一个有代表性的小区间,虽然说误差余项里面的x的取值是整个区大区间。

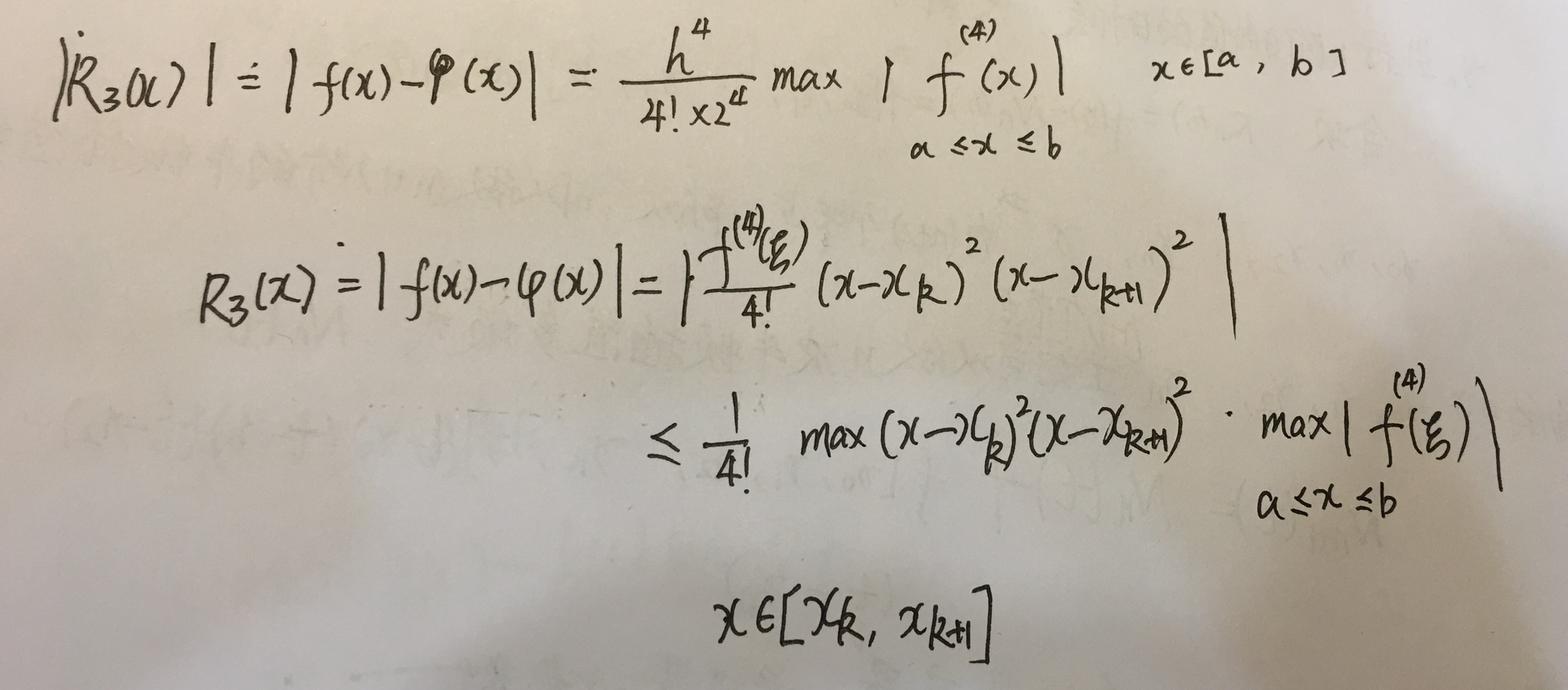

注解:
1. 3次样条插值也属于分段插值,它是分段插值的一种特例。
2.3次样条不是科学家提出来的,是造船工程师人员先提出来的,工程上的人先返发现的。
3. 连接点处1阶导数相同的话可以保证没有尖点,2阶导数代表弯曲程度,2阶导数相同的话曲率连续。高铁的时速400公里左右,曲率就很重要了,如果不注意的话可能会翻车。当达到一定速度的时候曲率就很重要了曲率的重要性就体现出来了。
4.赫尔米特插值需要知道所有连接点处的1阶导数值但是我们很多时候不能得到所有连接点的1阶导数值。
5.3次样条来源于造船,这里面有一个故事。船造好之后,工程师去采集一些船体上的点,在一个木板上放置一个软木条,用钉子按照采样点(的方位)依次固定这个软木条。那么软木条自然而然就会贴近这些点。此时,软木条就代表一个条曲线。这就是样条曲线的由来。科学家一看,这不就是一个插值问题吗?为何是插值问题呢?
答:a.采集的点相当于是样本点。b.曲线过这些点,说明这个曲线是插值曲线。c.导数必然是连续的,因为曲线不会有间断。d.具有很好曲率连续性,且不需要导数值。


注解:
1.3次样条插值是科学问题里面用的最多的插值方法。
2.定义4.3是数学家从工程(师)造船的实践中提取出来的一个数学上的定义。
3.S(x)开头的S代表:spline.
4.三次样条实际是分段插值,因为在固定软木条的时候,是依次固定,这就意味着样条是一段一段形成的,虽然整个是一个连续的样条曲线。
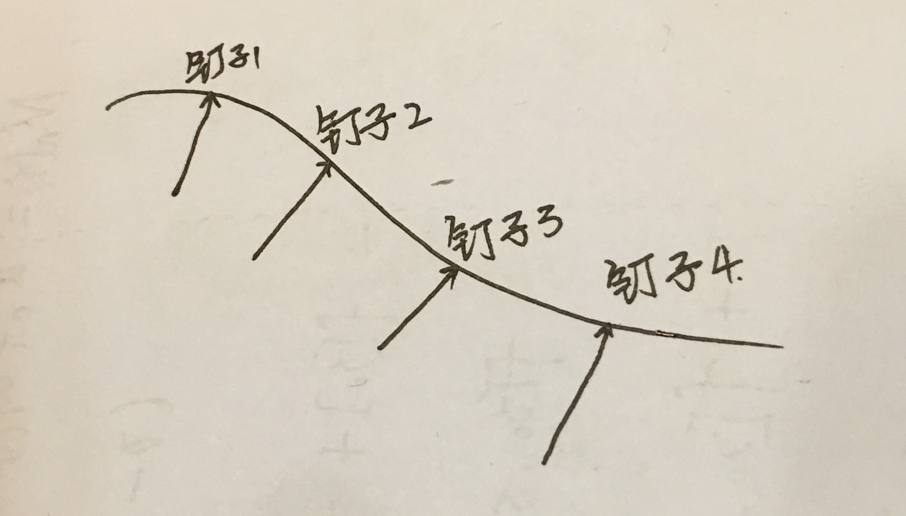
分段线性拉格朗日插值:有尖点。
分段3次Hermite插值:要求所有插值点有导数值。做出来的插值函数最多是1阶导数连续,2阶导数连续还不行。
3次样条:2阶导数连续,3次样条本身有2阶导数的,这是样条的特性。
3次样条插值的3个参考链接:
三次样条(cubic spline)插值 - 知乎 (zhihu.com)
矩阵与数值计算(13)——分段低次插值与三次样条插值 - 知乎 (zhihu.com)
三次样条插值在Python中的实现 - 知乎 (zhihu.com)
5.为什么强调S(x)是关于分划Δ的3次样条?为何S(x)不是1次样条,或者2次样条?
答:1次的话,求2阶导数就是0了,2次的话,求2阶导数后,就是一个常数了,常数的图像就不能发生变化了。
数学家或许是这样推出样条用3次做比较好的。当然也可以是4次,5次,6次,但是3次就行了,3次的话处理起来应该是比较简单的。
6.推广一下,如果提4次样条的定义,则第2条换成:S(x)在[a,b]上有3阶连续导数。如果提2次样条的定义也是可以的。用的最多的还是3次样条,因为计算简单。
7.3次样条函数和3次样条插值函数相比,只多了第3条的规定。
8.定义就是一个规定,定义的好坏取决于后面解决问题是不是得力。
9.3次样条插值函数的定义规定好之后,后面的事情就是看看符合这样定义的3次样条插值函数到底有没有,到底存在不。


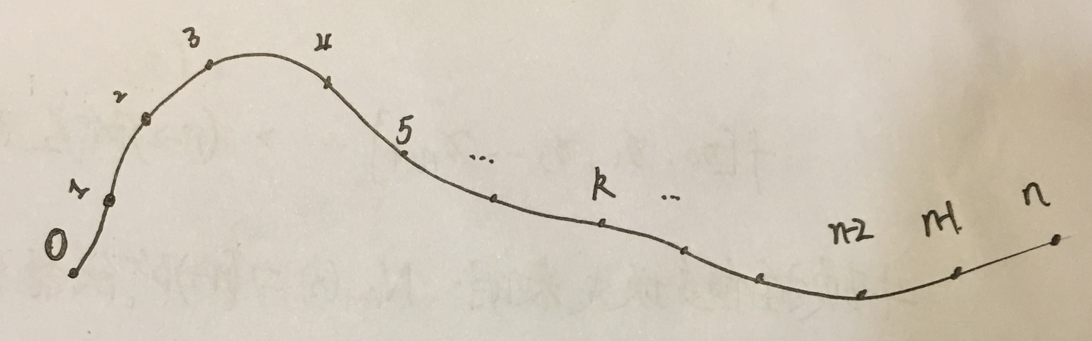
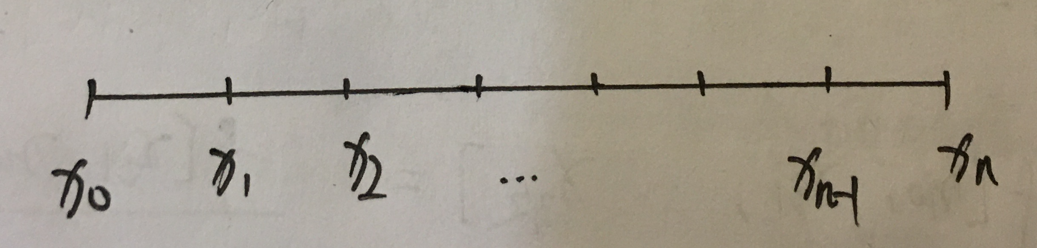
注解:
1.对于要知道的事情(3)的解释:在整个[a,b]区间上都有2阶连续导数,所以,x1到xn-1共n-1个内结点上自然也有2阶连续导数。有直到2阶连续导数,证明1阶导数也连续,证明函数也连续。
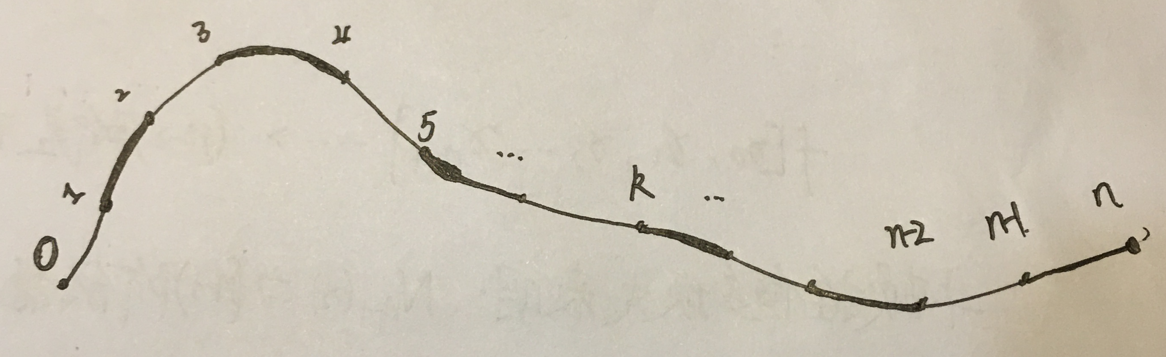
由于分段3次样条插值函数是拼接起来的,x1到xn-1共n-1个内结点上有直到2阶的连续导数,那么就意味着:在拼接点上,函数值相等,一阶导数值相等,二阶导数值相等,这就有了3(n-1)个条件了,也就相当于有了3(n-1)个方程了。
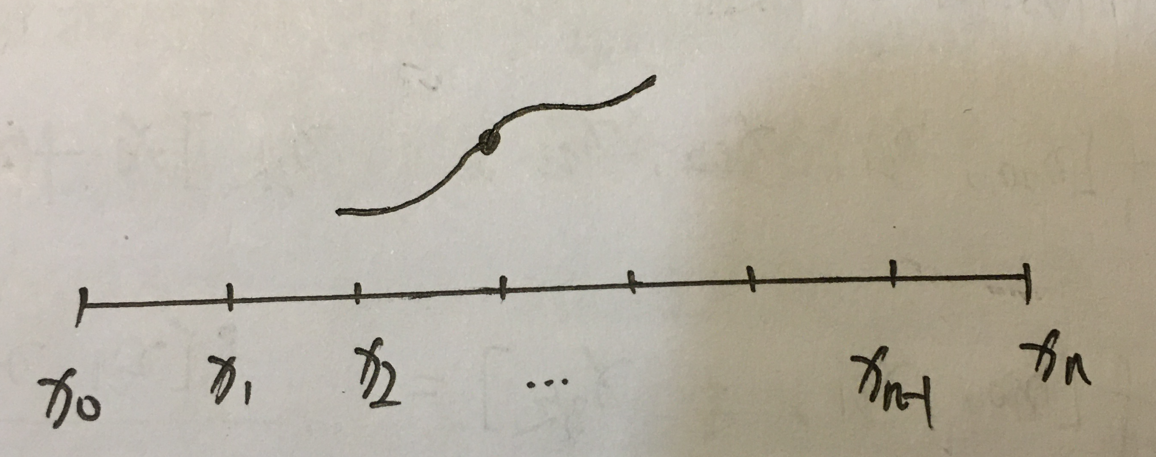
2.3次样条的边界条件也叫做3次样条的边值条件。

2阶导数是0,证明曲率是0,曲率是0证明函数图像是直线。
曲率就和二阶导数正相关了(请问函数在某一点处的二阶导数的几何意义是什么? 之前听人说是曲线在这一点的曲率,但是我感觉不太对啊? - 知乎 (zhihu.com))。
第一类条件为何叫自然条件?
答:海底地形可以用3次样条来建模,海边经过海水长时间的冲刷,边界是平的,是直线。所以是自然的边界条件。
第三类条件证明函数图像是有周期的,第三类条件适用于对周期函数的3次样条插值,首尾的信息相等。
假如不是对周期函数的插值,那么就用第一、二类边界条件。

下面对S(x)的推导来源于:三次样条(cubic spline)插值 - 知乎 (zhihu.com)


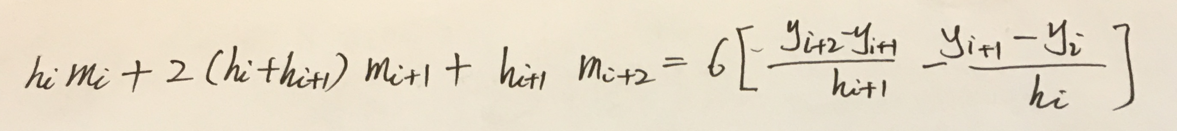
下面继续进行王兵团老师的学习:

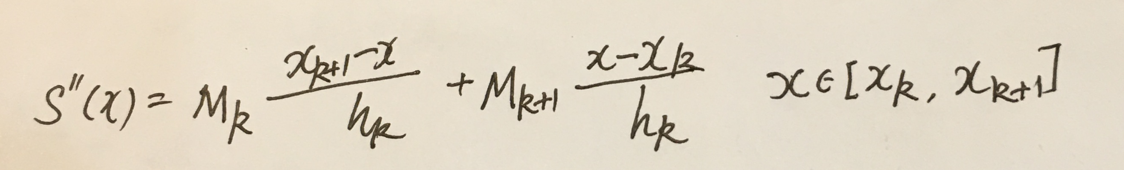
注解:
1.还是这个推导比较简洁。
2.连续两次积分的时候,是从xk开始积,积分到x
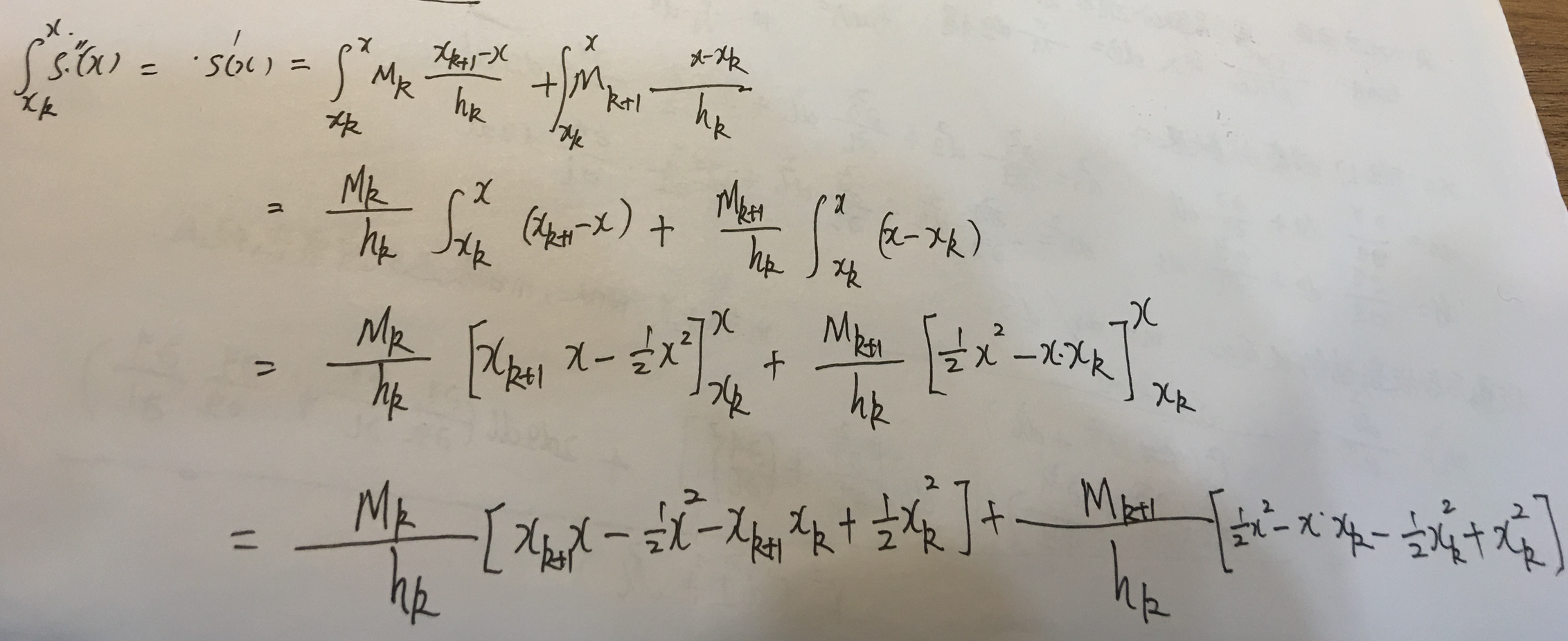
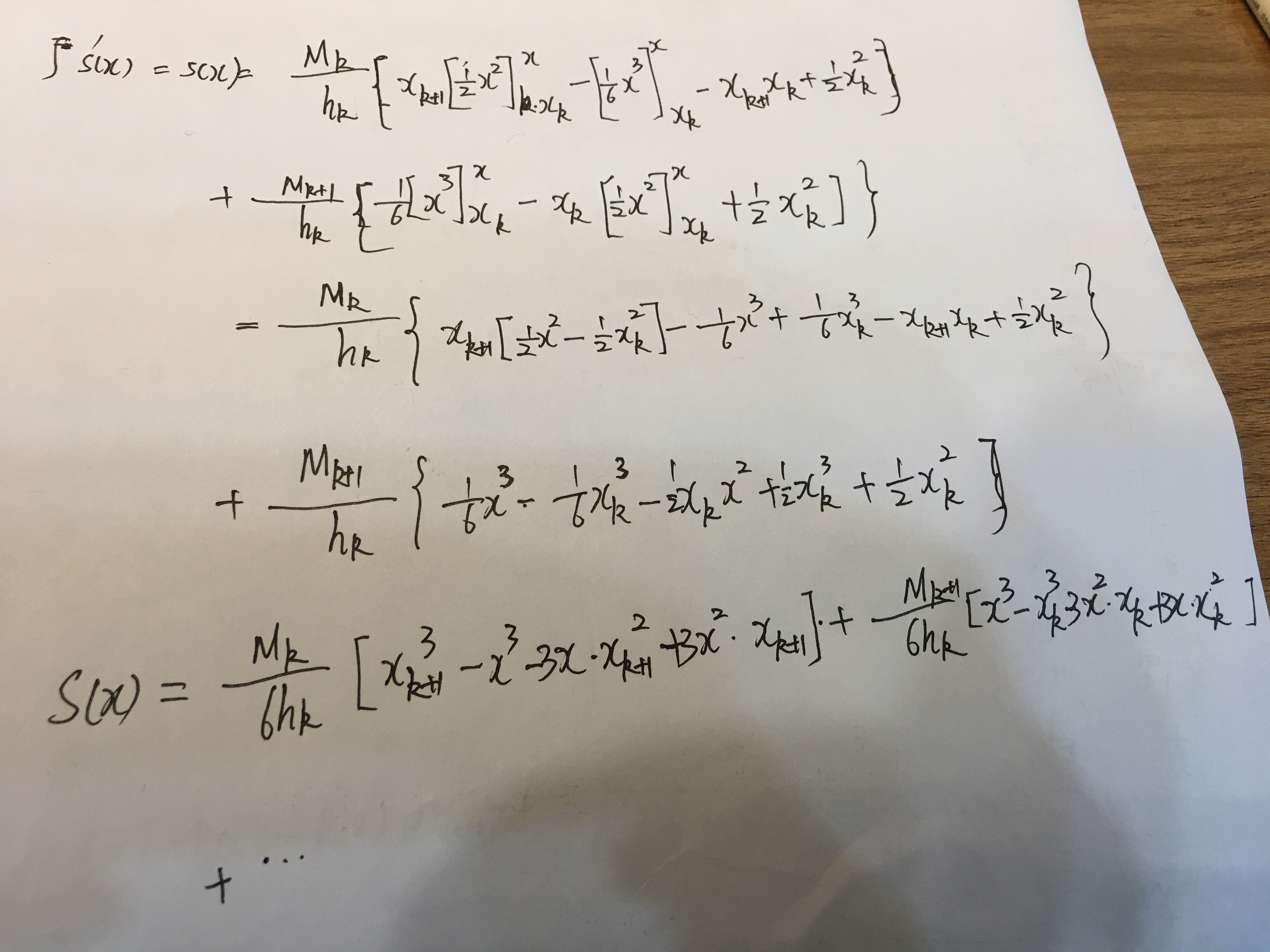

注解:
1.[a,b]区间上,1阶导数连续,就说明在[a,b]区间上的任何一点上,左导数=右导数。

注解:
1.函数的范数问题。向量是一个特殊的函数。所有向量问题可转变为函数问题。
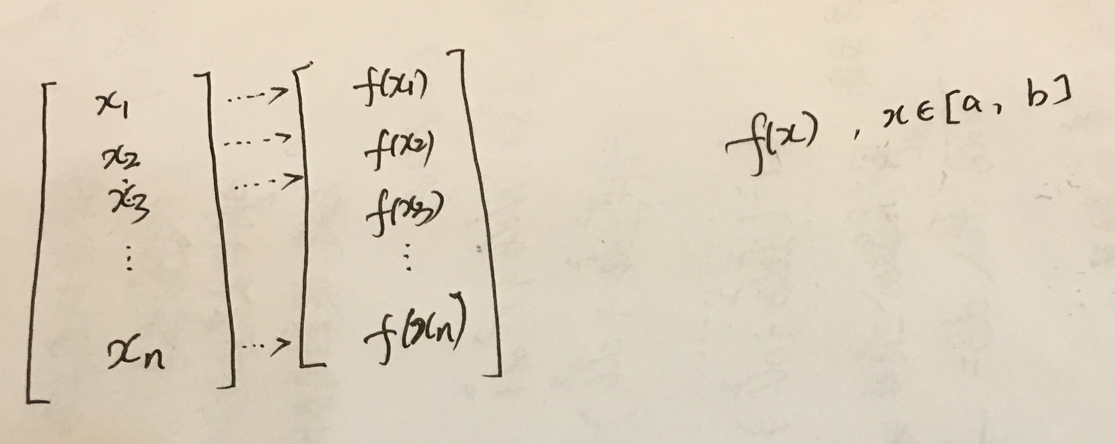
向量是有限个函数节点,有限个函数值。函数在一个连续定义域上,是有无限个节点和值的。
向量的无穷范数:
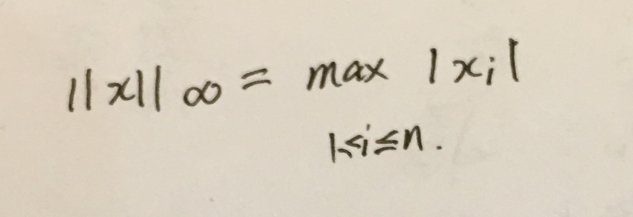
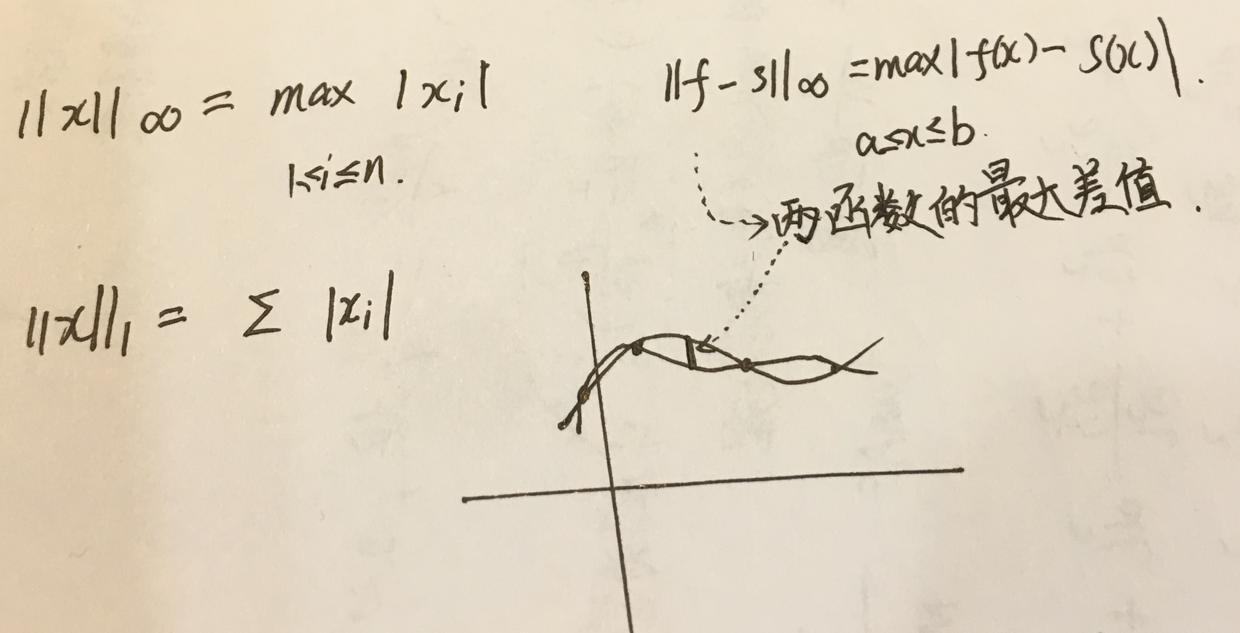
向量的一范是求和。
函数的一范就也是求和,和是什么?就是定积分。
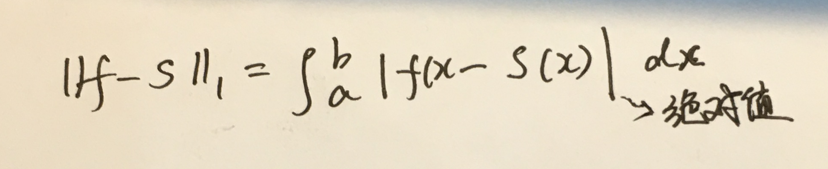
函数的二范:先平方,再求一个定积分。
函数是连续的东西,离散化的话,就能得到向量的一些结果。向量的东西一连续化就可以得到函数的东西。
2.h是步长。h4是很小的,说明逼近效果是很好的。3次样条不但函数逼近的很好,一阶导数和二阶导数也是有很好的逼近的。
至此,所有的插值理论已经讲完了。
反插值问题:略。
用插值方法求解一个特征多项式。略。
三角插值的提法;
指数插值的提法;
对数插值的提法。