机器学习02_逻辑回归作业

机器学习逻辑回归_02

---

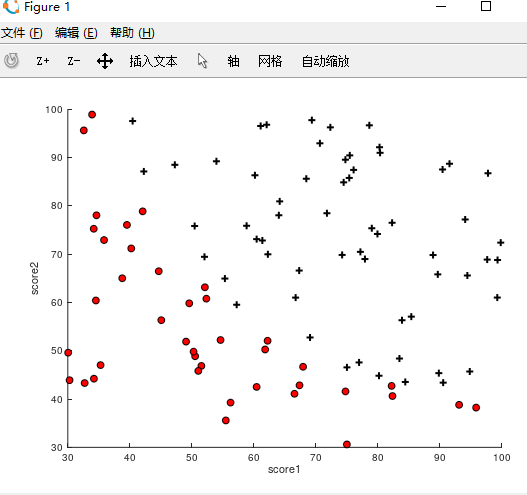
在本次逻辑回归作业中，我们将建立逻辑回归模型，通过学生的两门成绩，来预测该考生能都被大学录取。

---

I.数据可视化

将作业下载好后，打开octave，cd到machine-learning-ex2/ex2目录中，加载‘ex2data2.txt’（load）,编写plotData.m函数

function plotData(X, y)

figure; 
hold on;

% Find Indices of Positive and Negative Examples
pos = find(y==1); %找到y=1的行坐标
neg = find(y == 0);%找到y=2的行坐标
% Plot Examples
%画出通过的点  用 ‘+’ 表示
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, 'MarkerSize', 7);
%画出未通过的点 用‘o’ 表示
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'r', 'MarkerSize',7);

hold off;
end

---

II.编写逻辑回归假设函数

逻辑回归与线性回归的假设不同，逻辑回归的假设函数为

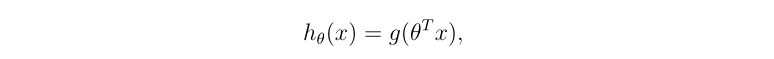
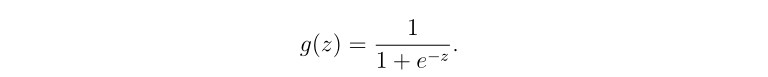
其中编写h(x)函数即sigmoid.m函数

function g = sigmoid(z)
%SIGMOID Compute sigmoid function
%   g = SIGMOID(z) computes the sigmoid of z.
% You need to return the following variables correctly 
g = zeros(size(z));

% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
%               vector or scalar).

g = 1./(1+ exp(-z));

end

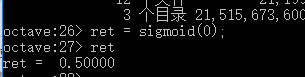
由上图可以看出当z为0是，g(z) = 1/2 = 0.5 检测函数如下图

---

III.编写cost & grad函数

根据下图公式，在costFunction.m中写出返回的J & grad

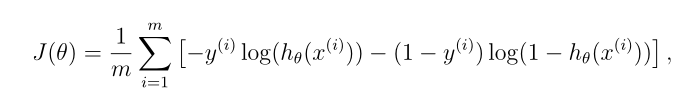
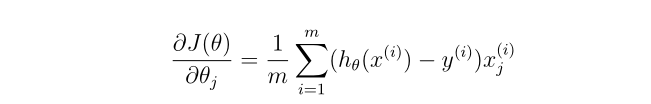
function [J, grad] = costFunction(theta, X, y)
m = length(y); 

J = 0;
grad = zeros(size(theta));
%sigmoid位阈值函数
J= -1 * sum( y .* log( sigmoid(X*theta) ) + (1 - y ) .* log( (1 - sigmoid(X*theta)) ) ) / m;

grad = ( X' * (sigmoid(X*theta) - y ) )/ m;               

end

---

IV.拟合函数的实现

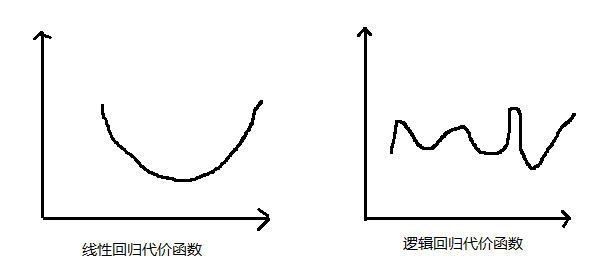
逻辑回归与线性回归不同，线性回归在寻找最优或者说最小J（花费时），由于J函数是完全凸函数，所以可以利用梯度下降算法找到最优解。而逻辑回归所J函数则不然(如下图)，无法利用传统的梯度下降算法找到最优解，所以我们要用到Octave中系统的fminunc自定义梯度下降的迭代次数来找到最优的解。

options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
plotDecisionBoundary(theta, X, y);

fminunc的参数说明：
1.@(t)(costFunction(t,X,y)) 是Octave中‘@’的句柄知识，大致可以理解为C语言中的指针。 2.initial_theta 设定好的初始值 3.options是指使用自定义的梯度下降公式‘GradObj’，以及400次的迭代次数(MaxIter)。

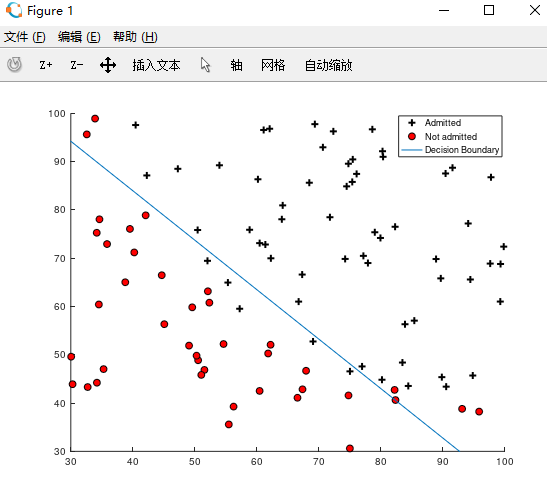
最后预测学生两门成绩分别为45,85是可以够录取。
Sorry =.=
忘记截屏啦。。。。。

机器学习第二次作业逻辑回归的附加作业会在下一次的博客中给出,今天出了点小问题。