转载至:https://blog.csdn.net/rekeless/article/details/82663767
二叉树的遍历分为深度优先遍历和广度优先遍历,其中,深度优先遍历又分为先序遍历,中序遍历和后序遍历三种。
先,中,后都是根据根节点而言的 ,即:
先序遍历:根——左——右
中序遍历:左——根——右
后序遍历:左——右——根
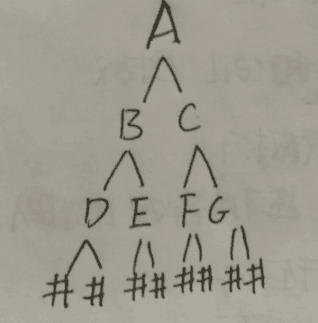
先序:ABDECFG
中序:DBEAFCG
后序:DEBFGCA
层次遍历:ABCDEFG
一 深度优先遍历递归实现
代码如下:
1 /* 2 calss Node{ 3 public: 4 Node(int v){ 5 val=v; 6 left=NULL; 7 right=NULL; 8 } 9 int val; 10 Node* left; 11 Node* right; 12 }; 13 14 */ 15 //先序遍历 16 void preOrder(Node * root){ 17 if(root==NULL) 18 return; 19 cout<<root->val; 20 preOrder(root->left); 21 preOrder(root->right); 22 } 23 //中序遍历 24 void inOrder(Node *root){ 25 if(root==NULL) 26 return; 27 inOrder(root->left); 28 cout<<root->val; 29 inOrder(root->right); 30 } 31 //后序遍历 32 void postOrder(Node *root){ 33 if(root=NULL) 34 return ; 35 postOrder(root->left); 36 postOrder(root->right); 37 cout<<root->val; 38 }
二 深度优先遍历非递归实现
深度优先遍历的非递归实现需要借助到栈作为辅助,代码如下
1 //先序遍历 2 void preOrder(Node root){ 3 if(root==NULL) 4 return ; 5 stack<Node*>s; 6 Node node=root; 7 while(!s.empty()||node!=NULL){ 8 if(node!=NULL){ 9 cout<<node->val; 10 s.push(node); 11 node=node->left; 12 }esle{ 13 node=s.top(); 14 s.pop(); 15 node=node->right; 16 }; 17 } 18 } 19 //中序遍历 20 void postOrder(Node* root){ 21 if(root==NULL) 22 return; 23 stack<Node*> s; 24 Node* node=root; 25 while(!s.empyu()||node!=NULL){ 26 if(node!=NULL){ 27 s.push(node); 28 node=node->left; 29 }else{ 30 node=s.top(); 31 s.pop(); 32 cout<<node->val; 33 node=node->right; 34 } 35 } 36 }
三 广度优先遍历非递归实现
//层次遍历方法非递归 void levelOrder(Node* root){ if(root==NULL)return; queue<Node*>q; q.push(root); while(!q.empty()){ Node * node=q.front(); q.pop(); cout<<node->val; if(q->left!=NULL)q.push(q->left); if(q->right!=NULL)q.push(q->right); } }
四 求二叉树的最长路径递归算法
1 int getlength(Node *root){ 2 if(root==NULL) 3 return 0; 4 else{ 5 int left=getlength(root->left); 6 int right=getlength(root->right); 7 return max(left,right)+1; 8 } 9 }
五 求二叉树的最长路径非递归算法
求二叉树最长路径的非递归算法其实是和层次遍历的逻辑一样的,算一下该二叉树有多少层就是最长路径,代码如下:
1 int getDepth(Node * root){ 2 if(root==NULL) 3 return 0; 4 else{ 5 //记录二叉树的高度 6 int depth=0; 7 //记录遍历到当前层的第几个节点 8 int num=0; 9 //记录当前层的节点个数 10 int count=1; 11 queue<Node*>q; 12 q.push(root); 13 while(!q.empty()){ 14 Node * node=q.front(); 15 num++; 16 if(node->left!=NULL)q.push(node->left); 17 if(node->right!=NULL)q.push(node->right); 18 if(num==count){ 19 depth++; 20 num=0; 21 count=queue.size(); 22 } 23 } 24 return depth; 25 } 26 }