一、什么是算法?
- 算法(Algorithm):一个计算过程,解决问题的方法

一个算法应该具有以下七个重要的特征:
- ①有穷性(Finiteness):算法的有穷性是指算法必须能在执行有限个步骤之后终止;
- ②确切性(Definiteness):算法的每一步骤必须有确切的定义;
- ③输入项(Input):一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输 入是指算法本身定出了初始条件;
- ④输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。没 有输出的算法是毫无意义的;
- ⑤可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行 的操作步,即每个计算步都可以在有限时间内完成(也称之为有效性);
- ⑥高效性(High efficiency):执行速度快,占用资源少;
- ⑦健壮性(Robustness):对数据响应正确。
二、时间复杂度:参考链接
1、时间复杂度举例说明
时间复杂度:就是用来评估算法运行时间的一个式子(单位)。一般来说,时间复杂度高的算法比复杂度低的算法慢。
类比生活中的一些时间,估计时间:

现在我们来说说下面这些代码的时间复杂度是多少呢?
print('hello world') print('hello python') print('hrllo ssd ') #O(1) 大O,简而言之可以认为它的含义是“order of”(大约是)。 # for i in range(n): print('hello world') for j in range(n): print('hello world') #O(n^2) for i in range(n): for j in range(i): print('hrllo owd') ##O(n^2) n= 64 while n>1: print(n) #O(log2n)或者O(logn) n = n//2 # while的分析思路: # 假如n = 64的时候会输出:如下图
# 这时候可以发现规律:
在n趋于无穷大的时候,任意两个不同底数的对数仅差一个常数。
所以从研究算法的角度log的底数不重要。
2、常见的算法时间复杂度(按照效率)由小到大依次为:
Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<O(n2logn)< Ο(n3)<…<Ο(2^n)<Ο(n!)
例如:

由图中我们可以看出,当 n 趋于无穷大时, O(nlogn) 的性能显然要比 O(n^2) 来的高
一般来说,只要算法中不存在循环语句,其时间复杂度就是 O(1)
而时间复杂度又分为三种:
- 最优时间复杂度 (Best-Case)
- 平均时间复杂度 (Average-Case)
- 最差时间复杂度 (Worst-Case)
最差时间复杂度的分析给了一个在最坏情况下的时间复杂度情况,这往往比平均时间复杂度好计算,而最优时间复杂度一般没什么用,因为没人会拿一些特殊情况去评判这个算法的好坏。
3、如何一眼判断时间复杂度?
- 循环减半的过程-》O(logn)
- 几次循环就是n的几次方的复杂度
三、空间复杂度
空间复杂度:用来评估算法内存占用大小的一个式子
四、对于递归的简单复习
1、递归最大的两个特点:
- 调用自身
- 结束条件
2、做个小练习来判断一下下面那些函数是递归函数?


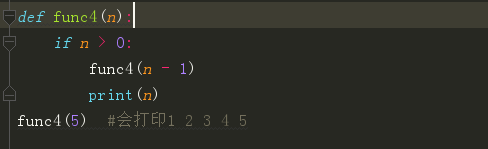
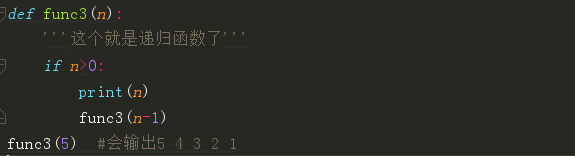
3、递归练习1

代码实现
def fun(n): if n>0: print("抱着",end="") fun(n-1) print("的我",end="") else: print("我的小鲤鱼",end="") fun(4)
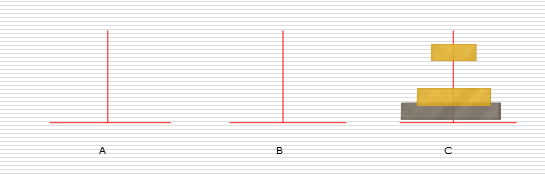
递归练习2:汉诺塔问题
解决思路:
假设有n个盘子:
- 1.把n-1个圆盘从A经过C移动到B
- 2.把第n个圆盘从A移动到C
- 3.把n-1个小圆盘从B经过A移动到C

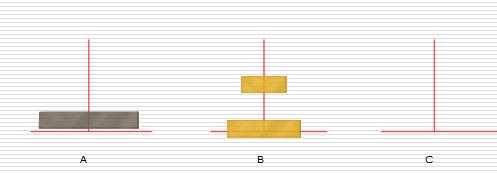
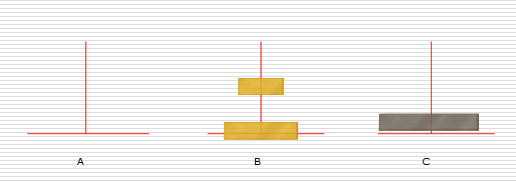
代码实现:
def func(n,a,b,c): if n==1: print(a,'-->',c) else: func(n-1,a,c,b) #将n-1个盘子从a经过c移动到b print(a,'-->',c) #将剩余的最后一个盘子从a移动到c func(n-1,b,a,c) #将n-1个盘子从b经过a移动到c n = int(input('请输入汉诺塔的层数:')) func(n,'柱子A','柱子B','柱子C')
总结:汉诺塔移动次数的递推式:h(x)=2h(x-1)+1


