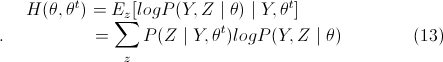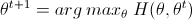EM算法简述
EM算法是一种迭代算法，主要用于含有隐变量的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由两步完成：
E步，求期望
M步，求极大。
EM算法的引入
如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法或贝叶斯估计法估计模型参数，但是当模型中含有隐变量时，就不能简单地使用这些估计方法。因此提出了EM算法。
EM算法流程
假定集合 
由观测数据 
和未观测数据 
组成， 
和 分别称为不完整数据和完整数据。假设Z的联合概率密度被参数化地定义为 
，其中 
表示要被估计的参数。 的最大似然估计是求不完整数据的对数似然函数
的最大值而得到的：
EM算法包括两个步骤：由E步和M步组成，它是通过迭代地最大化完整数据的对数似然函数 
的期望来最大化不完整数据的对数似然函数，其中：
假设在算法第t次迭代后 
获得的估计记为 
，则在(t+1)次迭代时，E-步：计算完整数据的对数似然函数的期望，记为：
M-步：通过最大化 
来获得新的 
。通过交替使用这两个步骤，EM算法逐步改进模型的参数，使参数和训练样本的似然概率逐渐增大，最后终止于一个极大点。
直观地理解EM算法，它也可被看作为一个逐次逼近算法：事先并不知道模型的参数，可以随机的选择一套参数或者事先粗略地给定某个初始参数，确定出对应于这组参数的最可能的状态，计算每个训练样本的可能结果的概率，在当前的状态下再由样本对参数修正，重新估计参数λ，并在新的参数下重新确定模型的状态，这样，通过多次的迭代，循环直至某个收敛条件满足为止，就可以使得模型的参数逐渐逼近真实参数。
可见上述算法流程中Q()是EM算法的核心，称为Q函数。
即完整数据的对数似然函数logP(x,y|)关于在给定观测数据x和当前参数下对未观测数据y的条件概率分布P(y|x,)的期望称为Q函数，
EM算法的导出
我们面对一个含有隐变量的概率模型，目标是极大化观测数据（不完全数据）x关于参数的对数似然函数，即极大化
L()=logP(x|)=logΣyP(X,y|)=log(ΣyP(X|y,)P(y|))
注意到这一极大化主要困难是式中有未观测数据并有包含和（或积分）的对数
示例
给定样本T = {X1, X2, …， Xm}，现在想给每个Xi一个Zi，即标出： {(X1,Z1), (X2,Z2),…，(Xm,Zm)}（z是隐形变量，zi=j可以看成是Xi被划分为j类），求对T的最大似然估计：
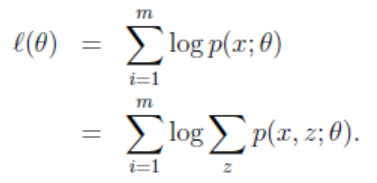
其实Zi也是个向量，因为对于每一个Xi，都有多种分类的情况。设第i个样本Xi在Z上的概率分布为Qi(Zi)，即Qi(Zi=j)表示Xi被划分到类j的概率，因此有ΣQi(Zi) = 1。
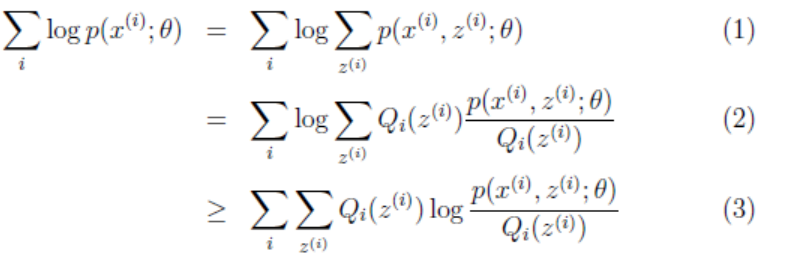
(2)到(3)是利用Jensen不等式，因为log(x)为凹函数，且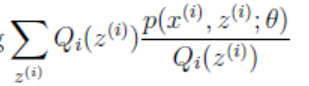
这个就是p（xi, zi; θ）/Qi(zi)的期望。
现在，根据Jensen不等式取等号的条件：
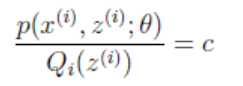
因为这个式子对于Zi等于任何值时都成立，且有ΣQi(Zi) = 1，所以可以认为：Σp(xi, zi;θ) = c。此时可以推出：
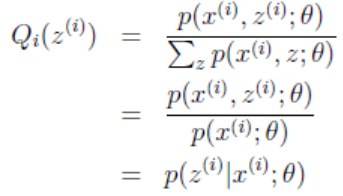
式子中，Zi是自变量，若θ已知，则可计算出Qi(zi)。
至此，终于可以描述算法过程了：
1）给θ一个初始值；
2）固定当前的θ，让不等式(3)取等号，算出Qi(zi)；-------> E 步
3）将2）算出的Qi(zi)代入g(Q, θ) =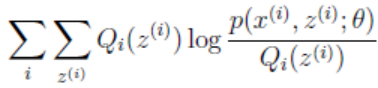 
，并极大化g(Q，θ)，得到新的θ。-------------->M步
4）循环迭代2）、3）至收敛。
证明EM算法收敛
当θ取到θt值时，求得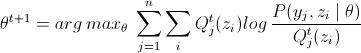
那么可得如下不等式：
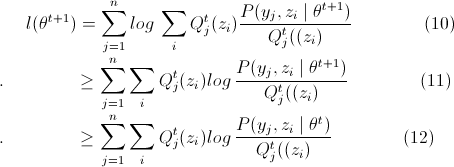
（10）=>（11）是因为Jensen不等式，因为等号成立的条件是θ为θt的时候得到的
，而现在
中的θ值为θt+1，所以等号不一定成立，除非θt+1=θt，
（11）=>（12）是因为θt+1已经使得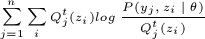
取得最大值，那必然不会小于（12）式。
所以l(θ)在迭代下是单调递增的，且很容易看出l(θ)是有上界的（单调有界收敛），则EM算法收敛性得证。
EM算法E步说明
上述EM算法描述，主要是参考Andrew NG教授的讲义，如果看过李航老师的《统计方法学》，会发现里面的证明以及描述表明上有些许不同，Andrew NG教授的讲义的说明（如上述）将隐藏变量的作用更好的体现出来，更直观，证明也更简单，而《统计方法学》中则将迭代之间θ的变化罗列的更为明确，也更加准确的描述了EM算法字面上的意思：每次迭代包含两步：E步，求期望；M步，求极大化。下面列出《统计方法学》书中的EM算法，与上述略有不同：
EM算法（2）：
选取初始值θ0初始化θ，t=0
Repeat {
E步：
M步：
}直到收敛
(13)式中，Y={y1,y2,...,ym},Z={z1,z2,...,zm},不难看出将（9）式中两个Σ对换，就可以得出（13）式，而（13）式即是关于分布z的一个期望值，而需要求这个期望公式，那么要求出所有的EM算法（1）中E步的值，所以两个表明看起来不同的EM算法描述其实是一样的。
总结：EM算法就是通过迭代地最大化完整数据的对数似然函数的期望，来最大化不完整数据的对数似然函数。
参考文献：
1.《统计学习方法》
2. http://blog.csdn.net/hechenghai/article/details/41896213
3.https://baike.baidu.com/item/em%E7%AE%97%E6%B3%95/1866163?fr=aladdin