js高阶函数应用—函数柯里化和反柯里化

在Lambda演算（一套数理逻辑的形式系统，具体我也没深入研究过）中有个小技巧：假如一个函数只能收一个参数，那么这个函数怎么实现加法呢，因为高阶函数是可以当参数传递和返回值的，所以问题就简化为：写一个只有一个参数的函数，而这个函数返回一个带参数的函数，这样就实现了能写两个参数的函数了（具体参见下边代码）——这就是所谓的柯里化（Currying，以逻辑学家Hsakell Curry命名），也可以理解为一种在处理函数过程中的逻辑思维方式。

function add(a, b) {
    return a + b;
}

//函数只能传一个参数时候实现加法
function curry(a) {
    return function(b) {
        return a + b;
    }
}
var add2 = curry(2); //add2也就是第一个参数为2的add版本
console.log(add2(3))//5

通过以上简单介绍我们大概了解了，函数柯里化基本是在做这么一件事情：只传递给函数一部分参数来调用它，让它返回一个函数去处理剩下的参数。用公式表示就是我们要做的事情其实是

fn(a,b,c,d)=>fn(a)(b)(c)(d)；

fn(a,b,c,d)=>fn(a，b)(c)(d)；

fn(a,b,c,d)=>fn(a)(b，c，d)；

......

再或者这样：

fn(a,b,c,d)=>fn(a)(b)(c)(d)()；

fn(a,b,c,d)=>fn(a)；fn(b)；fn(c)；fn(d)；fn()；

但不是这样：

fn(a,b,c,d)=>fn(a)；

fn(a,b,c,d)=>fn(a，b)；

......

这类不属于柯里化内容，它也有个专业的名字叫偏函数，这个之后我们也会提到。

下面我们继续把之前的add改为通用版本：

const curry = (fn, ...arg) => {
    let all = arg;
    return (...rest) => {
        all.push(...rest);
        return fn.apply(null, all);
    }
}
let add2 = curry(add, 2)
console.log(add2(8));    //10
add2 = curry(add);
console.log(add2(2,8)); //10

如果你想给函数执行绑定执行环境也很简单，可以多传入个参数：

const curry = (fn, constext, ...arg) => {
    let all = arg;
    return (...rest) => {
        all.push(...rest);
        return fn.apply(constext, all);
    }
}

不过到目前我们并没有实现柯里化，就是类似fn(a,b,c,d)=>fn(a)(b)(c)(d)，这样的转化，原因也很明显，我们curry之后的add2函数只能执行一次，不能够sdd2(5)(8)这样执行，因为我们没有在函数第一次执行完后返回一个函数，而是返回的值，所以无法继续调用。

所以我们继续实现我们的curry函数，要实现的点也明确了，柯里化后的函数在传入参数未达到柯里化前的个数时候我们不能返回值，应该返回函数让它继续执行（如果你阅读到这里可以试着自己实现一下），下面给出一种简单的实现方式：

const curry = (fn, ...arg) => {
    let all = arg || [],
        length = fn.length;
    return (...rest) => {
        let _args = all.slice(0); //拷贝新的all，避免改动公有的all属性，导致多次调用_args.length出错
        _args.push(...rest);
        if (_args.length < length) {
            return curry.call(this, fn, ..._args);
        } else {
            return fn.apply(this, _args);
        }
    }
}
let add2 = curry(add, 2)
console.log(add2(8));
add2 = curry(add);
console.log(add2(2, 8));
console.log(add2(2)(8));

let test = curry(function(a, b, c) {

console.log(a + b + c);

})

test(1, 2, 3);

test(1, 2)(3);

test(1)(2)(3);

这里代码逻辑其实很简单，就是判断参数是否已经达到预期的值（函数柯里化之前的参数个数），如果没有继续返回函数，达到了就执行函数然后返回值，唯一需要注意的点我在注释里写出来了all相当于闭包引用的变量是公用的，需要在每个返回的函数里拷贝一份；

好了到这里我们基本实现了柯里化函数，我们来看文章开始罗列的公式，细心的同学应该能发现：

fn(a,b,c,d)=>fn(a)(b)(c)(d)()；//mod1

fn(a,b,c,d)=>fn(a)；fn(b)；fn(c)；fn(d)；fn()；//mod2

这两种我们的curry还未实现，对于这两个公式其实是一样的，写法不同而已，对比之前的实现就是多了一个要素，函数执行返回值的触发时机和被柯里化函数的参数的不确定性，好了我们来简单修改一下代码：

const curry = (fn, ...arg) => {
    let all = arg || [],
        length = fn.length;
    return (...rest) => {
        let _args = all;
        _args.push(...rest);
        if (rest.length === 0) {
　　　　　　　all=[];
            return fn.apply(this, _args);
        } else {
            return curry.call(this, fn, ..._args);
        }
    }
}
let test = curry(function(...rest) {
    let args = rest.map(val => val * 10);
    console.log(args);
})
test(2);
test(2);
test(3);
test();
test(5);
test();
test(2)(2)(2)(3)(4)(5)(6)();
test(2, 3, 4, 5, 6, 7)();

现在我们这个test函数的参数就可以任意传，可多可少，至于在什么时候执行返回值，控制权在我们（这里是设置的传入参数为空时候触发函数执行返回值），当然根据这逻辑我们能改造出来很多我们期望它按我们需求传参、执行的函数——这里我们就体会到了高阶函数的灵活多变，让使用者有更多发挥空间。

到这里我们科里化基本说完了，下面我们顺带说一下偏函数，如果你上边柯里化的代码都熟悉了，那么对于偏函数的这种转化形式应该得心应手了：

fn(a,b,c,d)=>fn(a)；

fn(a,b,c,d)=>fn(a，b)；

我们还是先来看代码吧

function part(fn, ...arg) {
    let all = arg || [];
    return (...rest) => {
        let args = all.slice(0);
        args.push(...rest);
        return fn.apply(this, args)
    }
}

function add(a = 0, b = 0, c = 0) {
    console.log(a + b + c);
}
let addPart = part(add);
addPart(9); //9
addPart(9, 11);//20

很简单了，我们现在的addPar就能随便传参都能调用了，当然我们也能控制函数只调用某一个或者多个参数，例如这样：

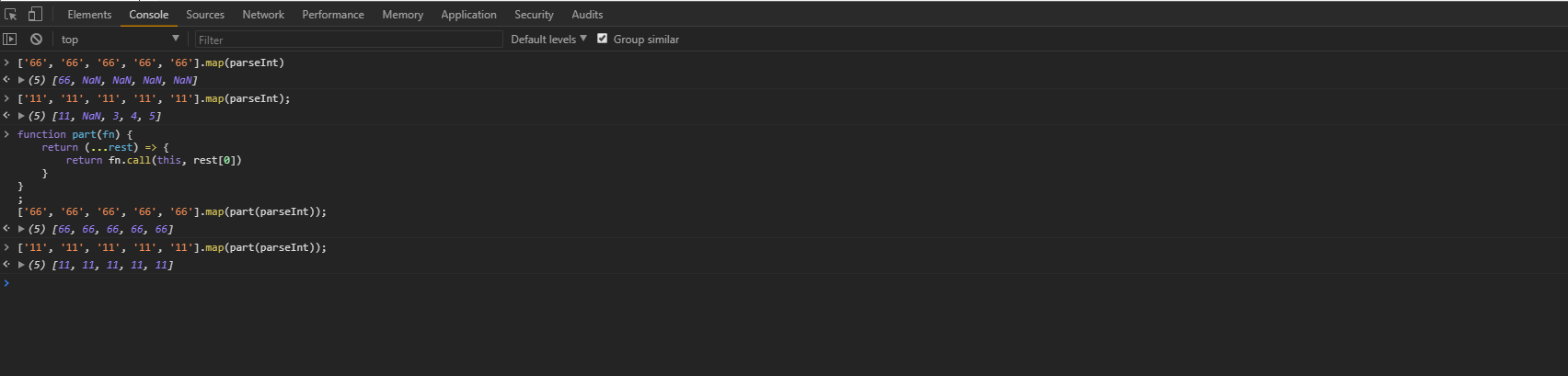
如上图所示，我们想用parseInt帮我们转化个数组，但是我们有没发改动parseInt的代码，所以控制一下传参就行了，这样我们map就传入的参数只取到第一个，得到了我们的期望值。

接着我们说一说反柯里化

鉴于时间较晚了，本来想写完的，还是打算先休息明晚再补上吧……