D [yLOI2019] 珍珠
Description
给定一个 deque,要求支持 push_back 和 push_front 操作,并且查询前缀与非和以及后缀与非和。
deque中只会有 (0) 或 (1),一共有 (n) 次操作,其中有 (m) 次操作给定,剩下的操作随机。
Limitations
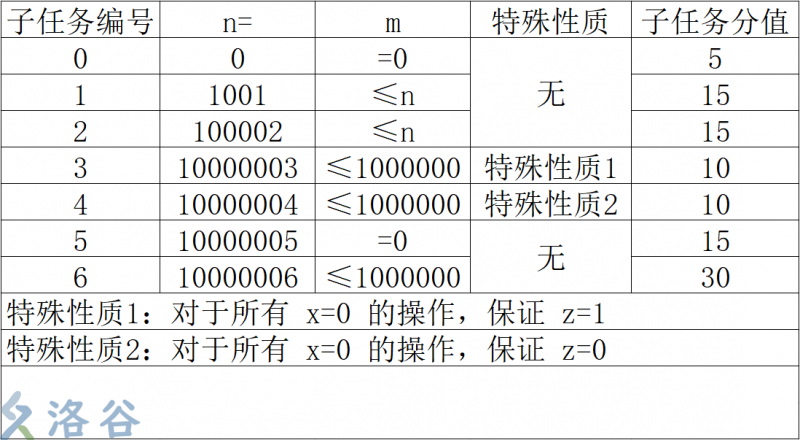
Solution
这是一道通过输入格式来防AK的题目
下面的做法只考虑前缀与非和,因为后缀的做法与前缀完全相同。
子任务 (0):
没有操作,输出四个 (0) 即可。期望得分 (5~pts)
子任务 (1):
暴力模拟,每次从前面插入的时候后面的元素暴力移位,暴力查询与非和即可。时间复杂度 (O(n^2)),期望得分 (15~pts)
子任务 (2):
考虑用线段树来维护每个区间的与非和,但是这样产生了一个问题,两个区间的与非和是无法合并的,因为与非运算没有交换律和结合律。
但是我们注意到事实上对于某个区间,序列的首部到区间左端点之前所有元素的与非和只可能是 (0) 或 (1),因此线段树每个节点维护两个信息:当该区间之前所有元素的与非和是 (0) 时与非上该区间的值,以及当该区间之前元素与非和是 (1) 时与非上该区间的值,然后即可 (O(1)) 转移。
时间复杂度 (O(n log n)),期望得分 (15 ~pts)
子任务 (3):
插入的元素全部是 (1)。
考虑一堆连续 (1) 的前缀与非和序列,一定形如 (101010101dots)
证明上,考虑第一个位置一定是 (1),然后 (1~ ext{nand}~1~=~0) ,(0~ ext{nand}~1~=~1),因此序列中 (0) 和 (1) 一定是循环出现的。
因此一个询问的答案一定是 (y~&~1)。时间复杂度 (O(n)),期望得分 (10~pts)
子任务 (4):
插入的元素全部是 (0)。
考虑一堆 (0) 的前缀与非和序列,一定形如 (011111111111 dots)
用与子任务 (3) 类似的办法即可解决。时间复杂度 (O(n)),期望得分 (10~pts)
子任务 (5):
考虑一个显而易见的事实,(0) 与非任何数都得 (1)。
因此考虑一次查询如果与非和的最后一项是 (0),则直接返回 (1) 即可。
同时对于最后一项是 (1) 的操作,只需要看这一项向前一共有连续的几个 (1),由于前面那一项是 (0),所以一段 (011111) 的序列的与非和一定是 (1010101010dots),而与 (0) 前面的项完全无关。
当然需要特判查询的 (0) 是序列第一个元素,以及查询的 (1) 前面没有 (0) 的情况。
那么问题就变成了对于每个位置维护它前面第一个 (0) 的位置。
由于 (m = 0) ,序列中的元素是完全随机的,因此连续 (0/1) 段的长度期望都是常数级的,因此暴力找即可,期望时间复杂度 (O(n)),期望得分 (15~pts)
子任务 (6):
考虑在序列不随机时怎么对每个数维护它前面第一个 (0) 的位置。
事实上,在每插入一个 (0) 时,都暴力修改这个 (0) 的有元素的一侧的连续 (1) 的信息即可。
例如,在序列左侧插入一个 (0),则暴力修改 (0) 右侧连续 (1) 的左侧最近的 (0) 的位置为该位置即可。在序列右侧插入同理。
考虑时间复杂度:每个为 (1) 的元素都只会在左侧最近和右侧最近的 (0) 插入的时候被修改信息,因此每个元素都只会被修改 (O(1)) 次信息,即每次均摊修改 (O(1)) 个信息,总的修改次数为 (O(n)),因此总时间复杂度 (O(n)),期望得分 (30~pts)。
appreciation
感谢@Burnside 神仙帮助进行题解的校对工作