【数论】中国剩余定理

百度百科

Pre-Knowledge

　　　　乘法逆元

 Definition&Solution

　　对于求解一元不定方程组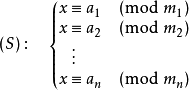的一种算法叫做中国剩余定理。又名孙子定理。

　　　求解方法：记tot=∏m_i，M_i=tot/a_i，即M_i为除a_i以外所有a的乘积。

　　　记t_i为M_i在Mod m_i意义下的逆元。求解单个逆元的方法见前置知识

　　　则方程组的唯一解为x≡Σ(a_i*t_i*M_i)　　(Mod tot)

　 　　下面的例题给出了一个中国剩余定理的典型应用

Example

传送门

Description

　　自从曹冲搞定了大象以后，曹操就开始捉摸让儿子干些事业，于是派他到中原养猪场养猪，可是曹冲满不高兴，于是在工作中马马虎虎，有一次曹操想知道母猪的数量，于是曹冲想狠狠耍曹操一把。举个例子，假如有16头母猪，如果建了3个猪圈，剩下1头猪就没有地方安家了。如果建造了5个猪圈，但是仍然有1头猪没有地方去，然后如果建造了7个猪圈，还有2头没有地方去。你作为曹总的私人秘书理所当然要将准确的猪数报给曹总，你该怎么办？

Input

　　第一行包含一个整数n表示 建立猪圈的次数，解下来n行，每行两个整数。表示建立了ai个猪圈，有bi头猪没有去处。你可以假定ai,aj互质.

Output

　　输出包含一个正整数，即为曹冲至少养母猪的数目。

Sample Input

3
3 1
5 1
7 2

Sample Output

16

Hint

　　n<=10;

　　bi<=ai<=1000

　　保证输入合法。

Solution

　　不难发现这是一道中国剩余定理的裸题。按照算法计算即可。

Code

#include<cstdio>
#define ll long long int
#define maxn 25

inline void qr(ll &x) {
    char ch=getchar();ll f=1;
    while(ch>'9'||ch<'0')    {
        if(ch=='-')    f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')    x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    x*=f;
    return;
}

inline ll max(ll a,ll b) {return a>b?a:b;}
inline ll min(ll a,ll b) {return a<b?a:b;}

inline void swap(ll &a,ll &b) {
    ll c=a;a=b;b=c;return;
}

ll n,m[maxn],ans,b[maxn],a[maxn],t[maxn],tot=1,x,y,MOD;

void exgcd(ll a,ll b,ll&fx,ll&fy) {
    if(!b) {
        MOD=a;fx=1;fy=0;return;
    }
    ll gx,gy;
    exgcd(b,a%b,gx,gy);
    fx=gy;
    fy=gx-(a/b)*gy;
    return;
}

int main() {
    qr(n);
    for(int i=1;i<=n;++i) {
        qr(a[i]);qr(b[i]);
        tot*=a[i];
    }
    for(int i=1;i<=n;++i) {
        m[i]=tot/a[i];
        a[i]*=-1;
        exgcd(m[i],a[i],t[i],y);
        a[i]*=-1;
        if(MOD<0)    t[i]=-t[i];
        while(t[i]<=0) t[i]+=a[i];
        ans+=b[i]*t[i]%tot*m[i]%tot;
        ans%=tot;
    }
    while(ans>0)    ans-=tot;
    while(ans<=0)　　ans+=tot;
    printf("%lld
",ans);
    return 0;
}