Description
有一个取数的游戏。初始时,给出一个环,环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后,将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏,两人轮流取数,取数的规则如下:
(1)选择硬币左边或者右边的一条边,并且边上的数非0;
(2)将这条边上的数减至任意一个非负整数(至少要有所减小);
(3)将硬币移至边的另一端。
如果轮到一个玩家走,这时硬币左右两边的边上的数值都是0,那么这个玩家就输了。
如下图,描述的是Alice和Bob两人的对弈过程,其中黑色节点表示硬币所在节点。结果图(d)中,轮到Bob走时,硬币两边的边上都是0,所以Alcie获胜。
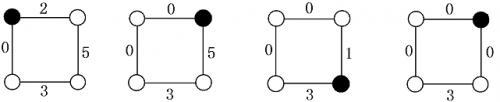
(a)Alice (b)Bob (c)Alice (d)Bob
现在,你的任务就是根据给出的环、边上的数值以及起点(硬币所在位置),判断先走方是否有必胜的策略。
Input
第一行一个整数N(N≤20),表示环上的节点数。
第二行N个数,数值不超过30,依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。
Output
仅一行。若存在必胜策略,则输出“YES”,否则输出“NO”。
Sample Input_1
4 2 5 3 0
Sample Output_1
YES
Sample Input_2
3 0 0 0
Sample Output_2
NO
Hint
(N≤20)
Solution
博弈论。有如下性质:
定理一:先手决定取数的方向。
证明:如图一: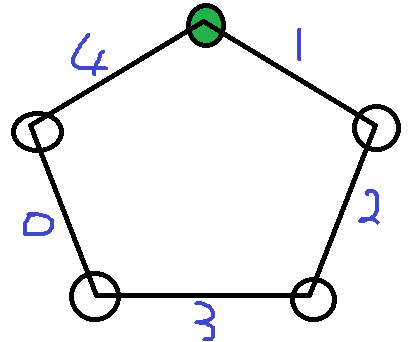 (图一)
(图一)
从绿色点开始取数,不妨设先手想顺时针方向取数,那么只需要把权值为1的边取成0即可。后手只能继续顺时针取数,因为不能取边权0的一侧。
一般的,先手只要将自己想要的方向取成0,那么就可以决定自己取数的方向。
定理2:取数过程的方向是单向的,一旦确定不会折返。
证明:
如图一,依然不妨设先手想顺指针取数,那么他先取了边权为1的边,此时后手只能继续顺时针取数,不管他将2取成1还是0,先手如果想继续顺时针取数,那么只需要继续取边权为3的边为0即可,无需考虑后手上一步是怎么取得。因为下一条边取成0之后,无论如何都不会返回上一条边了。
一般的,先手只要把自己经过的边取成0,就可以保证过程单向不会折返。
由定理1、2易推知定理3:在取数过程中,每个人会取到哪个位置是唯一确定的。
由定理2可以推知定理4:在取数过程中,谁的“前进道路”的下一条边是零边谁就会输。
证明:由定理2可知方向是单向的。如果前面是0边,则无法往前走,由定理二也无法往后走(只需要上一手的人把上一条边取成0)。于是会输。
综合定理1、2、3、4可以知道,只要出发点的取数方向一侧的线段离0边距离为偶数,则必胜,否则必输。由于先手可以选择顺时针或逆时针,所以枚举两个方向,如果有必胜策略则必胜。如果都会输则GG。
Code
#include<cstdio> #define maxn 25 inline void qr(int &x) { char ch=getchar();int f=1; while(ch>'9'||ch<'0') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); x*=f; return; } inline int max(const int &a,const int &b) {if(a>b) return a;else return b;} inline int min(const int &a,const int &b) {if(a<b) return a;else return b;} inline int abs(const int &x) {if(x>0) return x;else return -x;} inline void swap(int &a,int &b) { int c=a;a=b;b=c;return; } int n,MU[maxn]; int main() { qr(n);for(int i=1;i<=n;++i) qr(MU[i]); if(MU[1]) for(int i=1;i<=n;++i) { if(MU[i]==0) { if(!(i&1)) { putchar('Y');putchar('E');putchar('S');putchar(' ');return 0; } break; } } if(MU[n]) for(int i=n;i;--i) { if(MU[i]==0) { if(!((n-i+1)&1)) { putchar('Y');putchar('E');putchar('S');putchar(' ');return 0; } break; } } putchar('N');putchar('O');putchar(' '); return 0; }