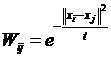机器学习降维算法四：Laplacian Eigenmaps 拉普拉斯特征映射

原创书写，转载请注明此文出自：http://www.cnblogs.com/xbinworld，http://blog.csdn.net/xbinworld

 

Laplacian Eigenmaps 

继续写一点经典的降维算法，前面介绍了PCA,LDA，LLE，这里讲一讲Laplacian Eigenmaps。其实不是说每一个算法都比前面的好，而是每一个算法都是从不同角度去看问题，因此解决问题的思路是不一样的。这些降维算法的思想都很简单，却在有些方面很有效。这些方法事实上是后面一些新的算法的思路来源。

Laplacian Eigenmaps[1] 看问题的角度和LLE有些相似，也是用局部的角度去构建数据之间的关系。

它的直观思想是希望相互间有关系的点（在图中相连的点）在降维后的空间中尽可能的靠近。Laplacian Eigenmaps可以反映出数据内在的流形结构。

Laplacian Eigenmaps也通过构建相似关系图（对应的矩阵为）来重构数据流形的局部结构特征。Laplacian Eigenmaps算法的主要思想是，如果两个数据实例i和j很相似，那么i和j在降维后目标子空间中应该尽量接近。设数据实例的数目为n，目标子空间的维度为m。定义大小的矩阵，其中每一个行向量是数据实例i在目标m维子空间中的向量表示，Laplacian Eigenmaps要优化的目标函数如下

定义对角矩阵，对角线上位置元素等于矩阵的第i行之和，经过线性代数变换，上述优化问题可以用矩阵向量形式表示如下：

其中矩阵是图拉普拉斯矩阵。限制条件保证优化问题有解，并且保证映射后的数据点不会被“压缩”到一个小于m维的子空间中。使得公式最小化的Y的列向量是以下广义特征值问题的m个最小非0特征值（包括重根）对应的特征向量：

 

使用时算法具体步骤为：

步骤1：构建图

使用某一种方法来将所有的点构建成一个图，例如使用KNN算法，将每个点最近的K个点连上边。K是一个预先设定的值。

步骤2：确定权重

确定点与点之间的权重大小，例如选用热核函数来确定，如果点i和点j相连，那么它们关系的权重设定为：

另外一种可选的简化设定是如果点i，j相连，否则。

步骤3：特征映射

计算拉普拉斯矩阵L的特征向量与特征值：

其中D是对角矩阵，满足，。

使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。

前面提到过，Laplacian Eigenmap具有区分数据点的特性，可以从下面的例子看出：

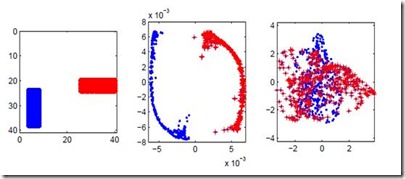
图1 Laplacian Eigenmap实验结果

见图1所示，左边的图表示有两类数据点（数据是图片），中间图表示采用Laplacian Eigenmap降维后每个数据点在二维空间中的位置，右边的图表示采用PCA并取前两个主要方向投影后的结果，可以清楚地看到，在此分类问题上，Laplacian Eigenmap的结果明显优于PCA。

 

图2 roll数据的降维

图2说明的是，高维数据（图中3D）也有可能是具有低维的内在属性的（图中roll实际上是2D的），但是这个低维不是原来坐标表示，例如如果要保持局部关系，蓝色和下面黄色是完全不相关的，但是如果只用任何2D或者3D的距离来描述都是不准确的。

下面三个图是Laplacian Eigenmap在不同参数下的展开结果（降维到2D），可以看到，似乎是要把整个带子拉平了。于是蓝色和黄色差的比较远。

 

 

Reference

[1] Belkin, M., Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Advances in neural information processing systems. 2002, 1585-592.