后缀数组

后缀数组

后缀数组，也就是后缀排序，是一个给字符串所有后缀排序的算法。

• 构造

  直接排序我们比较的是前 $ n $ 个字符的大小关系。为了优化这个过程，后缀数组用了一种倍增的思路。比较每个字符串的第一位，再比较前 2 位，再比较前 4 位... 最后得到整个数组。这样可以合理利用已经处理的结果。在比较前 $ 2 imes k $ 位的时候，其实就是做了一个双关键字排序：已经求出了所有后缀前 $ k $ 位的排名，那么对于第 $ i $ 个后缀它的双关键字分别是 $ rnk[i] , rnk[i+k] $。其中 $ rnk $ 表示一个后缀的排名。

  双关键字排序的过程往往用的是基数排序。准确地说，我们先把每个东西放进第一关键字的桶内，比较麻烦的处理方法是，从后往前从每个桶中按照第二关键字从大到小取出得到新的排名。但是这样不方便，可以先对桶做一次前缀和，这样的话第 $ i $ 个桶从上面取出一个元素的排名就是 $ S[i] $ ， 再把 $ S[i] $ 减一。

  注意，这里是认为两个相同关键字答案一样，实际上需要最后处理一下，把所有后缀排名设置为不同，否则会挂。

代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define MAXN 1000006
#define C 130
char ch[MAXN];
int sa[MAXN] , tp[MAXN] , rnk[MAXN] , buc[MAXN] , len;
void init(  ) {
    len = strlen( ch + 1 ); int m = C;
    for( int i = 1 ; i <= len ; ++ i ) ++ buc[rnk[i] = ch[i]];
    for( int i = 1 ; i <= m ; ++ i ) buc[i] += buc[i-1];
    for( int i = len ; i >= 1 ; -- i ) sa[buc[rnk[i]] --] = i;
    for( int k = 1 , p = 0 ; p < len ; k <<= 1 ) {
        p = 0;
        for( int i = 0 ; i <= m ; ++ i ) buc[i] = 0;
        for( int i = len - k + 1 ; i <= len ; ++ i ) tp[++p] = i;
        for( int i = 1 ; i <= len ; ++ i ) if( sa[i] > k ) tp[++p] = sa[i] - k;
        for( int i = 1 ; i <= len ; ++ i ) ++ buc[rnk[i]];
        for( int i = 1 ; i <= m ; ++ i ) buc[i] += buc[ i-1 ];
        for( int i = len ; i >= 1 ; -- i ) sa[buc[rnk[tp[i]]] --] = tp[i];
        p = 1;
        swap( rnk , tp );
        rnk[sa[1]] = 1;
        for( int i = 2 ; i <= len ; ++ i )
            rnk[sa[i]] = ( tp[sa[i]] == tp[sa[i-1]] && tp[sa[i] + k] == tp[sa[i-1] + k] ) ? p : ++ p;
        m = p;
    }
}

int main() {
    scanf("%s",ch+1);
    init();
    for( int i = 1 ; i <= len ; ++ i )
        printf("%d ",sa[i]);
}

复杂度是 $ O(nlog_2 n) $

height 数组

设 $ h[i] $ 表示排名为 $ i $ 的后缀和 排名为 $ i - 1 $ 的后缀的LCP

对于任意两个后缀 $ i , j $ 它们的 LCP $ LCP(suffix(i),suffix(j)) $ 就是 $ min(h[rnk[i]+1dots h[rnk[j]]]) $。

把后缀排序后的后缀写一起，那么

红色框内（也就是LCP）必然是相同的，毕竟再后缀排名中相邻。黄色框和绿色框必然不相同，因为LCP没有继续延申。但是由于黄色到绿色是有字符改变的 ，所以必然有个位置在黄色位发生了改变，这个位置的 height 就是LCP长度。所以取 min 是对的。

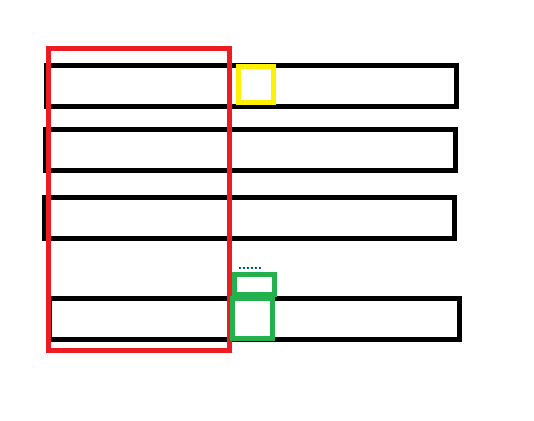
也就是说，对 $ h $ 进行 RMQ 后我们可以 $ O(1) $ 求出两个后缀的 LCP。

为了求 height 数组我们还需要一个结论：

$ height[rnk[i]] geq height[rnk[i-1]] - 1 $

分类讨论一下

• 如果 $ height[rnk[i-1]] leq 1 $ 由于 $ height $ 必然非负，它成立。

• 否则，即 $ height[rnk[i-1]] > 1 $ 那么

  

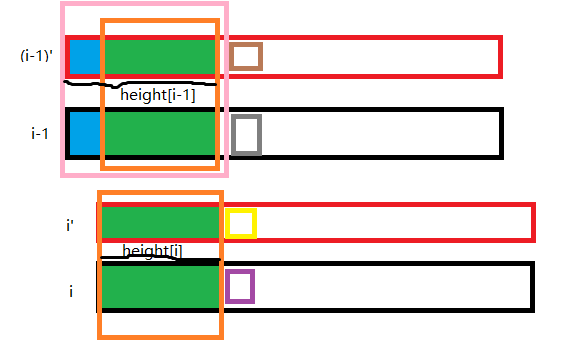
  图中 $ i'=height[i] $

  由于 $ height[rnk[i-1]] > 1 $ 那么必然有绿色块存在。此时，绿色块内的字符是一样的。$ i $ 可以由 $ i - 1 $ cut 一个字符得到，所以绿色与前面相同。其次，$ i' $ 和 $ i $ 的 LCP 长度必然至少是绿色块。我们知道褐色的字典序是小于灰色的，所以由 $ (i-1)' $ cut 首字母得到的串也一定在 $ i $ 前面。那么 $ i' $ 与 $ i $ 的 LCP 至少都是绿色块。当然也可能多于绿色块，因为可能 $ (i-1)' $ cut 首字母后得到的串和 $ i $ 之间还有其他串，所以黄色是可能等于紫色的。

这样就可以 $ O(n) $ 求出 height 了。存一个 last 表示到现在位置得到的 height ，然后对于第 $ i $ 个后缀从 last - 1 开始扫就好了。

for (i = 1, k = 0; i <= n; ++i) {
	if (k) --k;
	while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
	ht[rk[i]] = k;
}