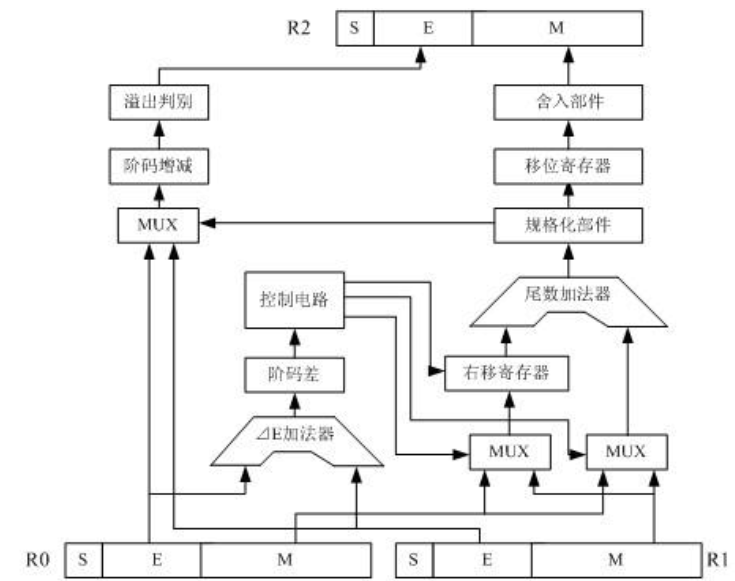
浮点数的加减运算一般由以下五个步骤完成:对阶、尾数运算、规格化、舍入处理、溢出判断
一、对阶
所谓对阶是指将两个进行运算的浮点数的阶码对齐的操作。对阶的目的是为使两个浮点数的尾数能够进行加减运算。因为,当进行M x·2Ex与M y·2Ey加减运算时,只有使两浮点数的指数值部分相同,才能将相同的指数值作为公因数提出来,然后进行尾数的加减运算。对阶的具体方法是:首先求出两浮点数阶码的差,即⊿E=E x-E y,将小阶码加上⊿E,使之与大阶码相等,同时将小阶码对应的浮点数的尾数右移相应位数,以保证该浮点数的值不变。几点注意:
(1)对阶的原则是小阶对大阶,之所以这样做是因为若大阶对小阶,则尾数的数值部分的高位需移出,而小阶对大阶移出的是尾数的数值部分的低位,这样损失的精度更小。
(2)若⊿E=0,说明两浮点数的阶码已经相同,无需再做对阶操作了。
(3)采用补码表示的尾数右移时,符号位保持不变。
(4)由于尾数右移时是将最低位移出,会损失一定的精度,为减少误差,可先保留若干移出的位,供以后舍入处理用。
二、尾数运算
尾数运算就是进行完成对阶后的尾数相加减。这里采用的就是我们前面讲过的纯小数的定点数加减运算。
三、结果规格化
在机器中,为保证浮点数表示的唯一性,浮点数在机器中都是以规格化形式存储的。对于IEEE754标准的浮点数来说,就是尾数必须是1.M的形式。由于在进行上述两个定点小数的尾数相加减运算后,尾数有可能是非规格化形式,为此必须进行规格化操作。
规格化操作包括左规和右规两种情况。
左规操作:将尾数左移,同时阶码减值,直至尾数成为1.M的形式。例如,浮点数0.0011·25是非规格化的形式,需进行左规操作,将其尾数左移3位,同时阶码减3,就变成1.1100·22规格化形式了。
右规操作:将尾数右移1位,同时阶码增1,便成为规格化的形式了。要注意的是,右规操作只需将尾数右移一位即可,这种情况出现在尾数的最高位(小数点前一位)运算时出现了进位,使尾数成为10.xxxx或11.xxxx的形式。例如,10.0011·25右规一位后便成为1.00011·26的规格化形式了。
四、 舍入处理
浮点运算在对阶或右规时,尾数需要右移,被右移出去的位会被丢掉,从而造成运算结果精度的损失。为了减少这种精度损失,可以将一定位数的移出位先保留起来,称为保护位,在规格化后用于舍入处理。
IEEE754标准列出了四种可选的舍入处理方法:
(1)就近舍入(round to nearest)这是标准列出的默认舍入方式,其含义相当于我们日常所说的“四舍五入”。例如,对于32位单精度浮点数来说,若超出可保存的23位的多余位大于等于100…01,则多余位的值超过了最低可表示位值的一半,这种情况下,舍入的方法是在尾数的最低有效位上加1;若多余位小于等于011…11,则直接舍去;若多余位为100…00,此时再判断尾数的最低有效位的值,若为0则直接舍去,若为1则再加1。
(2)朝+∞舍入(round toward +∞)对正数来说,只要多余位不为全0,则向尾数最低有效位进1;对负数来说,则是简单地舍去。
(3)朝-∞舍入(round toward -∞)与朝+∞舍入方法正好相反,对正数来说,只是简单地舍去;对负数来说,只要多余位不为全0,则向尾数最低有效位进1。
(4)朝0舍入(round toward 0)
即简单地截断舍去,而不管多余位是什么值。这种方法实现简单,但容易形成累积误差,且舍入处理后的值总是向下偏差。
五、 溢出判断
与定点数运算不同的是,浮点数的溢出是以其运算结果的阶码的值是否产生溢出来判断的。若阶码的值超过了阶码所能表示的最大正数,则为上溢,进一步,若此时浮点数为正数,则为正上溢,记为+∞,若浮点数为负数,则为负上溢,记为-∞;若阶码的值超过了阶码所能表示的最小负数,则为下溢,进一步,若此时浮点数为正数,则为正下溢,若浮点数为负数,则为负下溢。正下溢和负下溢都作为0处理。
要注意的是,浮点数的表示范围和补码表示的定点数的表示范围是有所不同的,定点数的表示范围是连续的,而浮点数的表示范围可能是不连续的。
六、例子
float a=0.3;b=1.6;
a=(0.3)10=(0011 1110 1001 1001 1001 1001 1001 1010)2 Sa=0 Ea=011 1110 1 Ma=1.001 1001 1001 1001 1001 1010
b=(1.6)10=(0011 1111 1100 1100 1100 1100 1100 1101)2 Sb=0 Eb=011 1111 1 Mb=1.100 1100 1100 1100 1100 1101
a+b=?
第一步:对阶
∵ Ea<Eb Eb-Ea=2
∴ Ma要调整为 0.0 1001 1001 1001 1001 1001 10 10
E=011 1111 1
第二步:尾数运算
0.01001100110011001100110
+ 1.10011001100110011001101
1.11100110011001100110011
第三步:规格化
1.11100110011001100110011已经是个规格化数据了
第四步:舍入处理
由于在对阶时,Ma有右移,且第一次最高为1,第二次为0,所以按"0舍1入",尾数运算结果调整为 1.11100110011001100110100
第五步:溢出判断
没有溢出,阶码不调整,所以最后的结果为
a+b=(0 01111111 11100110011001100110100)2=(0011 1111 1111 0011 0011 0011 0011 0100)2=(3FF33334)16
转为10进制
a+b=1.90000010
b-a=?
第一步:对阶
跟上面加法一样
第二步:尾数运算
1.10011001100110011001101
- 0.01001100110011001100110
1.01001100110011001100111
第三步:规格化
1.01001100110011001100111已经是个规格化数据了
第四步:舍入处理
由于在对阶时,Ma有右移,且第一次最高为1,第二次为0,所以按"0舍1入",尾数运算结果调整为 1.01001100110011001100110
第五步:溢出判断
没有溢出,阶码不调整,所以最后的结果为
a-b=(0 01111111 01001100110011001100110)2=(0011 1111 1010 0110 0110 0110 0110 0110)2=(3FA66666)16
转为10进制
a-b=1.29999995
付:浮点运算加法器逻辑电路