For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes root1 and root2.
Example 1:
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.
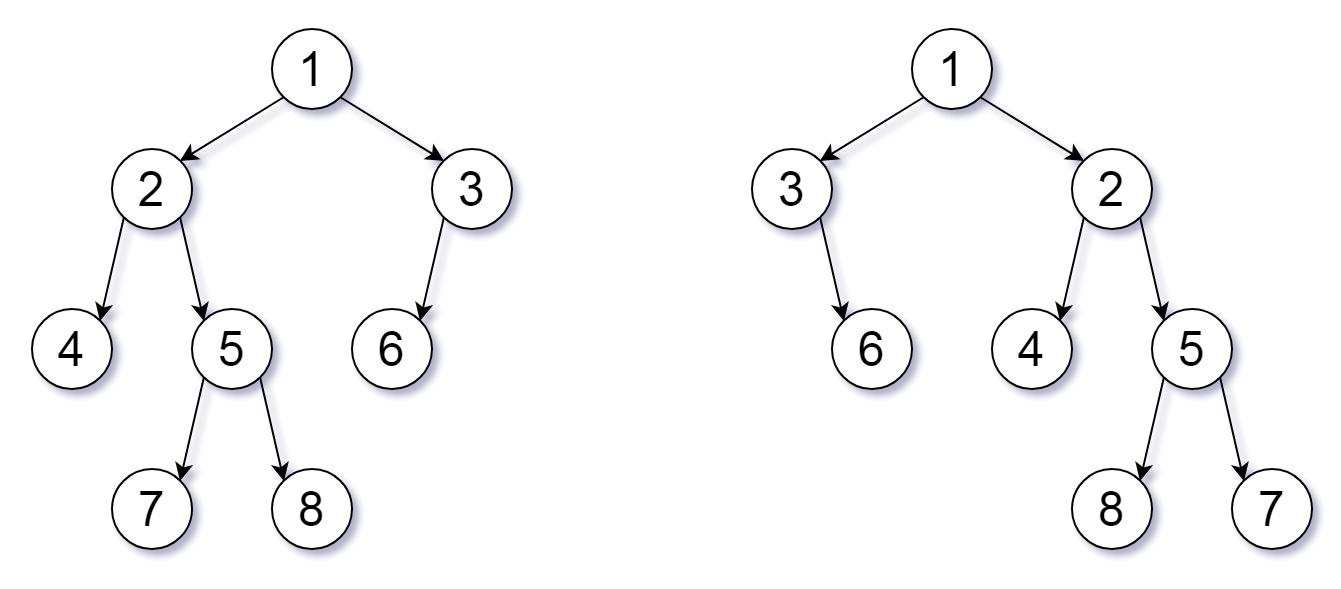
Note:
- Each tree will have at most
100nodes. - Each value in each tree will be a unique integer in the range
[0, 99].
A、B两颗二叉树相等当且仅当rootA->data == rootB->data,且A、B的左右子树相等或者左右互换相等
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: bool flipEquiv(TreeNode* root1, TreeNode* root2) { if (!root1 && !root2) return 1; if ((!root1&&root2) || (root1 && !root2)) return 0; if (root1&&root2) { if (root1->val == root2->val) { if (flipEquiv(root1->left, root2->left)) return flipEquiv(root1->right, root2->right); else if (flipEquiv(root1->left, root2->right)) return flipEquiv(root1->right, root2->left); } } return 0; } };