Description
ZS the Coder is playing a game. There is a number displayed on the screen and there are two buttons, ' + ' (plus) and '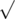 ' (square root). Initially, the number 2 is displayed on the screen. There are n + 1 levels in the game and ZS the Coder start at the level 1.
' (square root). Initially, the number 2 is displayed on the screen. There are n + 1 levels in the game and ZS the Coder start at the level 1.
When ZS the Coder is at level k, he can :
- Press the ' + ' button. This increases the number on the screen by exactly k. So, if the number on the screen was x, it becomes x + k.
- Press the '
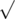 ' button. Let the number on the screen be x. After pressing this button, the number becomes
' button. Let the number on the screen be x. After pressing this button, the number becomes 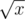 . After that, ZS the Coder levels up, so his current level becomes k + 1. This button can only be pressed when x is a perfect square, i.e. x = m2 for some positive integer m.
. After that, ZS the Coder levels up, so his current level becomes k + 1. This button can only be pressed when x is a perfect square, i.e. x = m2 for some positive integer m.
Additionally, after each move, if ZS the Coder is at level k, and the number on the screen is m, then m must be a multiple of k. Note that this condition is only checked after performing the press. For example, if ZS the Coder is at level 4 and current number is 100, he presses the '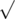 ' button and the number turns into 10. Note that at this moment, 10 is not divisible by 4, but this press is still valid, because after it, ZS the Coder is at level 5, and 10 is divisible by 5.
' button and the number turns into 10. Note that at this moment, 10 is not divisible by 4, but this press is still valid, because after it, ZS the Coder is at level 5, and 10 is divisible by 5.
ZS the Coder needs your help in beating the game — he wants to reach level n + 1. In other words, he needs to press the ' ' button ntimes. Help him determine the number of times he should press the ' + ' button before pressing the '
' button ntimes. Help him determine the number of times he should press the ' + ' button before pressing the ' ' button at each level.
' button at each level.
Please note that ZS the Coder wants to find just any sequence of presses allowing him to reach level n + 1, but not necessarily a sequence minimizing the number of presses.
The first and only line of the input contains a single integer n (1 ≤ n ≤ 100 000), denoting that ZS the Coder wants to reach level n + 1.
Print n non-negative integers, one per line. i-th of them should be equal to the number of times that ZS the Coder needs to press the ' + ' button before pressing the ' ' button at level i.
' button at level i.
Each number in the output should not exceed 1018. However, the number on the screen can be greater than 1018.
It is guaranteed that at least one solution exists. If there are multiple solutions, print any of them.
3
14
16
46
2
999999999999999998
44500000000
4
2
17
46
97
In the first sample case:
On the first level, ZS the Coder pressed the ' + ' button 14 times (and the number on screen is initially 2), so the number became2 + 14·1 = 16. Then, ZS the Coder pressed the ' ' button, and the number became
' button, and the number became 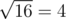 .
.
After that, on the second level, ZS pressed the ' + ' button 16 times, so the number becomes 4 + 16·2 = 36. Then, ZS pressed the ' ' button, levelling up and changing the number into
' button, levelling up and changing the number into 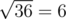 .
.
After that, on the third level, ZS pressed the ' + ' button 46 times, so the number becomes 6 + 46·3 = 144. Then, ZS pressed the ' ' button, levelling up and changing the number into
' button, levelling up and changing the number into 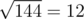 .
.
Note that 12 is indeed divisible by 4, so ZS the Coder can reach level 4.
Also, note that pressing the ' + ' button 10 times on the third level before levelling up does not work, because the number becomes6 + 10·3 = 36, and when the '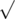 ' button is pressed, the number becomes
' button is pressed, the number becomes 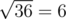 and ZS the Coder is at Level 4. However, 6 is not divisible by 4 now, so this is not a valid solution.
and ZS the Coder is at Level 4. However, 6 is not divisible by 4 now, so this is not a valid solution.
In the second sample case:
On the first level, ZS the Coder pressed the ' + ' button 999999999999999998 times (and the number on screen is initially 2), so the number became 2 + 999999999999999998·1 = 1018. Then, ZS the Coder pressed the '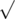 ' button, and the number became
' button, and the number became 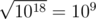 .
.
After that, on the second level, ZS pressed the ' + ' button 44500000000 times, so the number becomes 109 + 44500000000·2 = 9·1010. Then, ZS pressed the ' ' button, levelling up and changing the number into
' button, levelling up and changing the number into 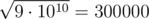 .
.
Note that 300000 is a multiple of 3, so ZS the Coder can reach level 3.
题意:note说的已经很明白了(逃)
解法:找规律,我们可以发现4, 36, 144, 400符合规律,再仔细看一下,就是 [i(i + 1)]2,
那么已经明确了,ans=i*(i+1)表示前一个开始数字,[i(i + 1)]2
是下一个,求出差除以i就行,当然需要化简一下
#include <bits/stdc++.h>
using namespace std;
string s;
map<int,int>q;
int main()
{
long long n;
cin>>n;
if(n==1)
{
cout<<"2"<<endl;
}
else
{
cout<<"2"<<endl;
long long ans=2;
for(long long i=2;i<=n;i++)
{
cout<<(i+1)*i*(i+1)-ans/i<<endl;
ans=i*(i+1);
}
}
return 0;
}