You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.
We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 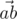 and
and 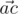 is acute (i.e. strictly less than
is acute (i.e. strictly less than 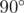 ). Otherwise, the point is called good.
). Otherwise, the point is called good.
The angle between vectors 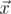 and
and 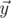 in 5-dimensional space is defined as
in 5-dimensional space is defined as 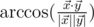 , where
, where 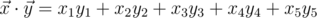 is the scalar product and
is the scalar product and 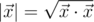 is length of
is length of 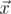 .
.
Given the list of points, print the indices of the good points in ascending order.
The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.
The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103) — the coordinates of the i-th point. All points are distinct.
First, print a single integer k — the number of good points.
Then, print k integers, each on their own line — the indices of the good points in ascending order.
6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1
1
3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0
0
In the first sample, the first point forms exactly a 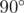 angle with all other pairs of points, so it is good.
angle with all other pairs of points, so it is good.
In the second sample, along the cd plane, we can see the points look as follows:
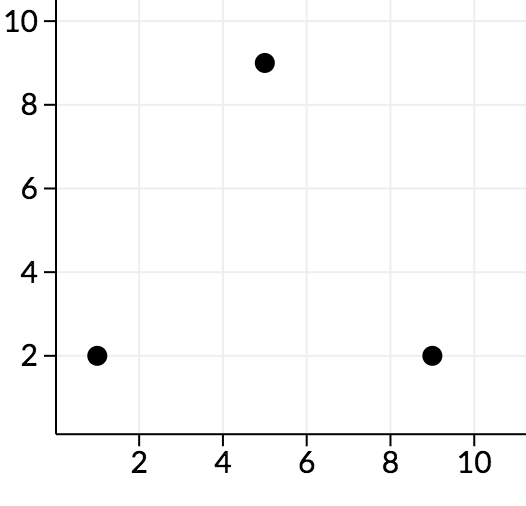
We can see that all angles here are acute, so no points are good.
题意:坏点:一个点和它周围的点形成的角度有一个小于90,问有多少好点,五维的环境下哦
解法:
1 二维的环境下 一个点周围是4个点,三维的环境下,一个点周围是6个点,那么..五维的环境应该是10个点,包括本身是11点,超过11点都不算
2 然后暴力计算
#include<bits/stdc++.h> using namespace std; int x[1230][6]; int y[1230][6]; int n; vector<int>Ve; int main(){ cin>>n; for(int i=1;i<=n;i++){ for(int j=1;j<=5;j++){ cin>>x[i][j]; } } if(n>=12){ cout<<"0"<<endl; return 0; } for(int i=1;i<=n;i++){ memset(y,0,sizeof(y)); int flag=0; for(int j=1;j<=n;j++){ if(i==j) continue; for(int k=1;k<=5;k++){ y[j][k]=x[j][k]-x[i][k]; // cout<<y[j][k]<<"A"<<endl; } for(int k=1;k<j;k++){ int sum=0; if(k==i) continue; for(int l=1;l<=5;l++){ sum+=y[k][l]*y[j][l]; } if(sum>0){ flag=1; break; } } if(flag){ break; } } if(flag==0){ Ve.push_back(i); } } int Size=Ve.size(); cout<<Size<<endl; for(int i=0;i<Size;i++){ cout<<Ve[i]<<endl; } return 0; }