【转载】VC维，结构风险最小化

以下文章转载自http://blog.sina.com.cn/s/blog_7103b28a0102w9tr.html

如有侵权，请留言，立即删除。

1 VC维的描述和理解

给定一个集合S={x1,x2,...xd}，如果一个假设类H（hypothesis h ∈ H）能够实现集合S中所有元素的任意一种标记方式，则称H能够打散S。有了打散的定义，就得到VC维的定义：H的VC维表示能够被H打散的最大集合的大小。若H能分散任意大小的集合，那么VC(H)为无穷大。

​VC维反应的是hypothesis space的容量，容量度量的是空间的复杂度，表达能力，方程集合的灵活性，这种度量是通过评估hypothesis space中成员的wiggly程度实现的。

以二维线性分类器​为例进行说明，其VC维就等于3，即最多能够将三个样本的集合打散，无法将四个样本的集合打散。

对于三个样本点：对其​进行二分类标记，有2^3=8种方式，分别是：

{A→-1,BC→+1}，{A→+1,BC→-1}

{B→-1,AC→+1}，{B→+1,BC→-1}

{C→-1,AB→+1}，{C→+1,BC→-1}

{ABC→-1}，{ABC→+1}

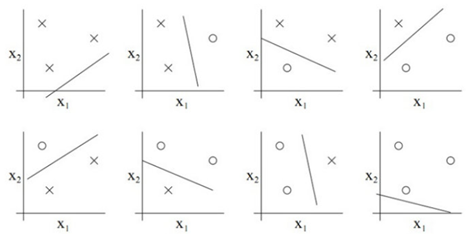
用图片表示，情况如下：

 

对于四个点的情况：二维分类器就无法实现打散。四个点时，有2^4=16种分法，一堆一个点另一堆三个点（1，3）；两两均分（2，2）；一堆四个另一堆没有（0，4）三种情况。

第一种情况，有如下八种分法：​

​{A→-1,BCD→+1}，{A→+1,BCD→-1}

{B→-1,ACD→+1}，{B→+1,ACD→-1}

{C→-1,ABD→+1}，{C→+1,ABD→-1}

{D→-1,ABC→+1}，{D→+1,ABC→-1}

第三种情况，有两种分法：

{ABCD→-1}

{ABCD→+1}

对第二种情况，没有办法实现对所有可能的情况进行分类，可以实现的情况有四种：

​{AB→-1,CD→+1}，{AB→+1,CD→-1}

{AC→-1,BD→+1}，{AC→+1,BD→-1}

但是无法实现AD一堆，BC一堆的分类。所以总共可以实现14种分法，不满足16种，二维平面上找不到四个点可以被线性分类器被打散。

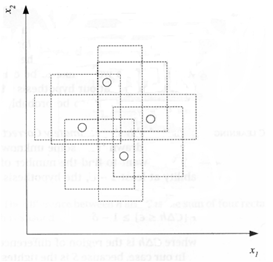
但是注意，二维平面中并不是只有线性分类器一种模型，例如，以下图为例说明，与坐标平行的矩形可以打散四个点，所以二维空间中与坐标平行的矩形假设空间的VC维是4。​

 

2 结构风险最小化

2.1 经验风险最小化

​预测与问题真实解之间的误差，就叫做风险（更严格的说，误差的累积叫做风险）。选择了一个假设之后（更直观点说，得到了一个分类器以后），真实误差无从得知，但可以用某些可以掌握的量来逼近它。最直观的想法就是使用分类器在样本数据上的分类的结果与真实结果（因为样本是已经标注过的数据，是准确的数据）之间的差值来表示。这个差值叫做经验风险R_emp(w)。

以前的机器学习方法都把经验风险最小化作为努力的目标，但后来发现很多分类函数能够在样本集上轻易达到100%的正确率，在真实分类时却一塌糊涂（即所谓的推广能力差，或泛化能力差）。此时的情况便是选择了一个足够复杂的分类函数（它的VC维很高），能够精确的记住每一个样本，但对样本之外的数据效果很差。

此原则适用的大前提是经验风险要确实能够逼近真实风险才行，但实际上能逼近么？答案是不能，因为样本数相对于现实世界要分类的文本数来说简直九牛一毛，经验风险最小化原则只在这占很小比例的样本上做到没有误差，当然不能保证在更大比例的真实文本上也没有误差。​

2.2 结构风险最小化

​为了解决经验风险最小化中存在的问题，引入泛化误差界的概念。

该思想认为，真实风险​应该由两部分内容刻画，一是经验风险，代表了分类器在给定样本上的误差；二是置信风险，代表了在多大程度上可以信任分类器在未知文本上分类的结果。很显然，第二部分是没有办法精确计算的，因此只能给出一个估计的区间，也使得整个误差只能计算上界，而无法计算准确的值（所以叫做泛化误差界，而不叫泛化误差）。

其中，​置信风险与两个量有关，一是样本数量，显然给定的样本数量越大，学习结果越有可能正确，此时置信风险越小；二是分类函数的VC维，显然VC维越大，推广能力越差，置信风险会变大。

泛化误差界的公式为：

R(w)≤R_emp(w)+Ф(n/h)​

​公式中R(w)就是真实风险，R_emp(w)就是经验风险，Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小，即结构风险最小。

我的理解是，关于置信风险，样本数量增多，​会降低置信风险，但同时为了保证准确率，会是VC维升高，不利于置信风险的降低；降低VC维，模型就会相对简单，不能保证在样本数量较多的时候的正确率。所以这两种之间需要权衡，找到平衡点。

此外，结构风险中包含的经验风险和置信风险，我觉得也可以理解成训练误差和模型复杂度的问题。经验风险是模型在已有样本上的误差，置信风险中利用VC维对模型的复杂度进行度量，并希望能够尽量降低复杂度，增加模型的泛化能力，使得模型的测试误差降低。