设计思想
1.输入整型数组(1000个元素)
2.动态规划实现最大子数组之和
3.加入int32类型的数值溢出判断
4.输出最大子数组之和和其位置。
一.对于一个元素个数较小的int数组,没有int32数组溢出判断
1 #include<iostream>
2 using namespace std;
3 int main()
4 {
5 int n,star=0,end=0;
6 //实现整型数组的输入
7 cout<<"输入整型数组的长度";
8 cin>>n;
9 int *p=new int[n];
10 cout<<"输入一个整型数组";
11 for(int i=0;i<n;i++)
12 {
13 cin>>p[i];
14 }
15 int sum=p[0];
16 int max_sum=p[0];
17 //copy的csdn上大神的代码。注释为自己理解
18 for(int i=1;i<n;i++)
19 {
20 if(sum>0) //从第二个数开始判断是否为正数
21 {
22 sum=sum+p[i]; //是正数,将和值(初始值为p【0】)和第i+1个数做和。
23 if(sum>max_sum) // 并判断是否为最大,是让其赋值给max_sum,并将子数组末位置改变。
24 {
25 max_sum=sum;
26 end=i;
27 }
28 }
29 else
30 {
31 sum=p[i]; //是负数,将第i+1个数的值赋值给和值sum
32 if(sum>max_sum)//并判断是否为最大,是让其赋值给max_sum,并将子数组初、末位置改变。
33 {
34 max_sum=sum;
35 star=i;
36 end=i;
37 }
38 }
39 }
40 cout<<"最大子数组位置为第"<<star+1<<"个到第"<<end+1<<"个"<<endl;
41 cout<<"最大子数组和为"<<max_sum<<endl;
42 return 0;
43 }
结果截图:

二.一个1000元素个数的数组(为了测试输入便利,利用随机数及随机数种子实现1000个元素),加入int32类型判断溢出
1 #include<iostream>
2 #include<stdlib.h>
3 #include <time.h>
4 using namespace std;
5 int main()
6 {
7 int n=1000,star=0,end=0;
8 //利用随机数实现1000个元素,用随机数只是便于输入1000个元素的数组。
9 int *p=new int[n];
10 srand((unsigned)time(NULL));
11 for(int i=0;i<n;i++)
12 {
13 p[i]=rand()%1000-500;
14 }
15 //打印这个1000个元素的数组
16 for(int i=0;i<n;i++)
17 {
18 cout<<p[i]<<" ";
19 if((i+1)%10==0)
20 {
21 cout<<endl;
22 }
23 }
24 int sum=p[0];
25 int max_sum=p[0];
26 //copy的csdn上大神的代码。注释为自己理解
27 for(int i=1;i<n;i++)
28 {
29 if(sum>0) //从第二个数开始判断是否为正数
30 {
31 if(p[i]>(INT_MAX-sum)) //加入了一段判断int类型数据是否溢出。
32 {
33 cout<<"int类型溢出"<<endl;
34 return 0;
35 }
36 sum=sum+p[i]; //是正数,将和值(初始值为p【0】)和第i+1个数做和。
37 if(sum>max_sum) // 并判断是否为最大,是让其赋值给max_sum,并将子数组末位置改变。
38 {
39 max_sum=sum;
40 end=i;
41 }
42 }
43 else
44 {
45 sum=p[i]; //是负数,将第i+1个数的值赋值给和值sum
46 if(sum>max_sum)//并判断是否为最大,是让其赋值给max_sum,并将子数组初、末位置改变。
47 {
48 max_sum=sum;
49 star=i;
50 end=i;
51 }
52 }
53 }
54 cout<<"最大子数组位置为第"<<star+1<<"个到第"<<end+1<<"个"<<endl;
55 cout<<"最大子数组和为"<<max_sum<<endl;
56 return 0;
57 }
结果截图:
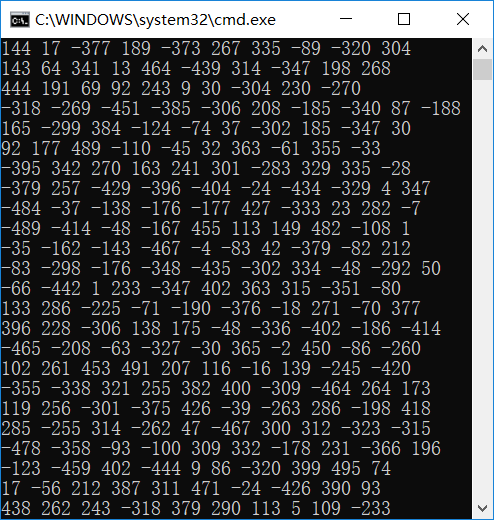
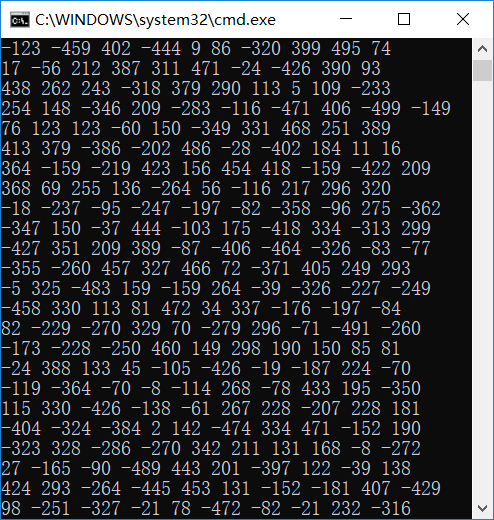
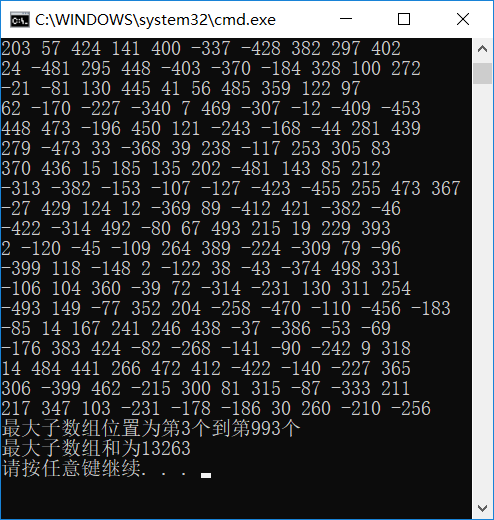
三.为了测试出int32类型溢出,将随机数扩大10^6倍
1 #include<iostream>
2 #include<stdlib.h>
3 #include <time.h>
4 using namespace std;
5 int main()
6 {
7 int n=1000,star=0,end=0;
8 //利用随机数实现1000个元素,用随机数只是便于输入1000个元素的数组。
9 int *p=new int[n];
10 srand((unsigned)time(NULL));
11 for(int i=0;i<n;i++)
12 {
13 p[i]=rand()%1000-500;
14 p[i]=p[i]*1000000;
15 }
16 //打印这个1000个元素的数组
17 for(int i=0;i<n;i++)
18 {
19 cout<<p[i]<<" ";
20 if((i+1)%10==0)
21 {
22 cout<<endl;
23 }
24 }
25 int sum=p[0];
26 int max_sum=p[0];
27 //copy的csdn上大神的代码。注释为自己理解
28 for(int i=1;i<n;i++)
29 {
30 if(sum>0) //从第二个数开始判断是否为正数
31 {
32 if(p[i]>(INT_MAX-sum)) //加入了一段判断int类型数据是否溢出。
33 {
34 cout<<"int类型溢出"<<endl;
35 return 0;
36 }
37 sum=sum+p[i]; //是正数,将和值(初始值为p【0】)和第i+1个数做和。
38 if(sum>max_sum) // 并判断是否为最大,是让其赋值给max_sum,并将子数组末位置改变。
39 {
40 max_sum=sum;
41 end=i;
42 }
43 }
44 else
45 {
46 sum=p[i]; //是负数,将第i+1个数的值赋值给和值sum
47 if(sum>max_sum)//并判断是否为最大,是让其赋值给max_sum,并将子数组初、末位置改变。
48 {
49 max_sum=sum;
50 star=i;
51 end=i;
52 }
53 }
54 }
55 cout<<"最大子数组位置为第"<<star+1<<"个到第"<<end+1<<"个"<<endl;
56 cout<<"最大子数组和为"<<max_sum<<endl;
57 return 0;
58 }
结果截图:
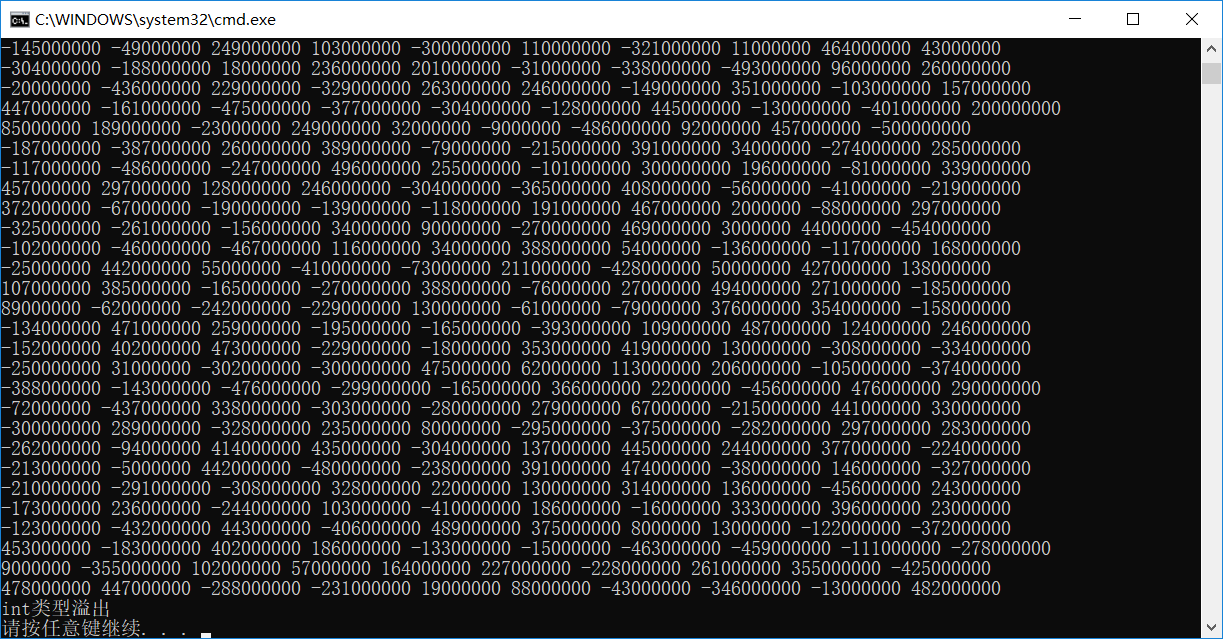
总结
对于解决最大子数组之和的问题有一定的算法,但实际实现成代码形式有很大困难,最后借鉴网上大神的代码并理解才能实现。估计2个半小时,实际用时近3个小时。团队合作帮助很大。