编译过程
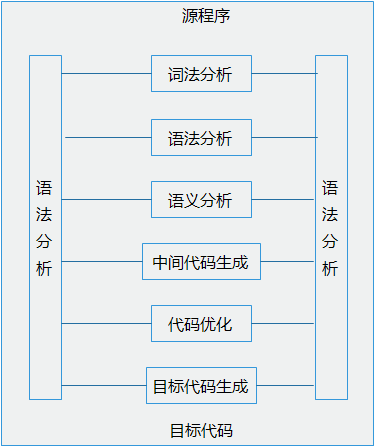
词法分析:对源程序从前到后(从左至右)逐个字符地扫描,从而识别出一个个"单词"符号。
语法分析:判断语法是否出错,如表达式、循环语句、程序等。
语义分析:检查如赋值语句左右是否匹配,是否有零除数等。
文法
G={Vt*Vn*S*P}
Vt是一个非空有限的符号集合,它的每个元素称为终结符。
Vn是一个非空有限集合的符号,它的每个元素称为非总结符。
S称为文法G的开始符号。
P是一个非空有限集合,它的元素称为产生式。
1型文法:又称为上下文有关文法。
2型文法:又称为上下文无关文法。
3型文法:又称为正规文法,使用最多。
0型文法:短语文法。
有限自动机
计算机控制系统的控制程序具有有限状态自动机(FA)的特征,可以用有限状态机理论来描述。
确定有限自动机(DFA)
自动机的每个状态都有对字母表中所有符号的转移。
非确定有限自动机(NFA)
自动机的状态对字母表中的每个符号可以有也可以没有转移,对一个符号甚至可以有多个转移。
(1)确定的有限自动机DFA
S是一个有限状态集合。
是一个字母表,输入字符的集合。
f是从S*àS上的单值部分映像。f(A,a)=Q表示当前状态为A,输入为a时,将转换到下一状态Q,称Q为A的一个后继状态。
S0S,是唯一的初态。
ZS,是一个终态集。
已知有DFA M1=({s0,s1,s2,s3},{a,b},f,S,{s3})
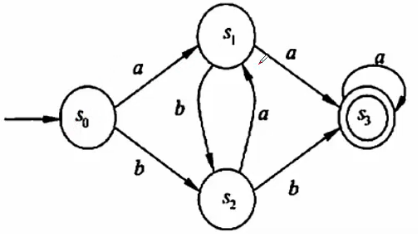
(2)不确定的有限自动机NFA
S是一个有限状态集合。
是一个字母表,输入字符的集合。
f是从S*àS上的单值部分映像。f(A,a)=Q表示当前状态为A,输入为a时,将转换到下一状态Q,称Q为A的一个后继状态。
S0S,是一个非空初态集。
ZS,是一个终态集。
正规式
下面文法G[S]它无法识别(D),次文法对应正规式为(C)。
G[S]:
SàaA|bB
AàbS|b
BàaS|a
(1)A.ababab B.bababa C.abbaab D.babba
(2)A.(a|b)* B.(ab)* C.(ab|ba)* D.(ab)*b*
解析:
SàaAàabSàabaAàababSà(ab)*
SàbBàbaSàbabBàbabaSà(ba)*
SàaAàabSàabbBàabbaSàabbaaAàabbaabà(ab|ba)*
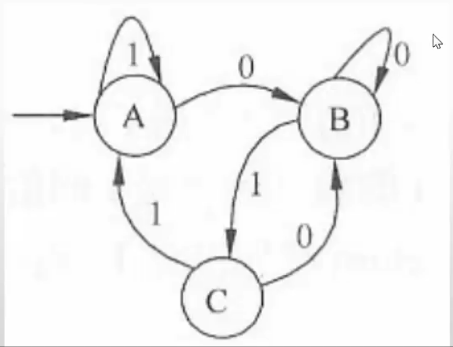
下图所示为一个有限自动机(其中,A是初态,C是终态),该自动机识别的语言可用正规式(C)表示。
A.0000 B.1111 C.0101 D.1010
对于以下编号为 j,k,l的正规式,正确的说法是(C)。
j(aa*|ab)*b k(a|b)*b l((a|b)*|aa)*b
A.正规式j,k等价 B.正规式j,l等价
C.正规式k,l等价 D.正规式j,k,l互不等价
语法树
以图示化形式把句子分解成各个组成部分,以分析句子的语法结构。语法树表示法与文法规则完全一致。但更为直观和完整。
满足下列条件的数称为文法G的语法树:
(1)每个节点用G的一个终结符或非终结符标记。
(2)根结点用文法开始符号S标记。
(3)内部结点一定是非终结符。若某个内部结点A有n个分支,且其所有子节点从左至右依次标记为X1,X2,…,Xn,则AàX1,X2,…,Xn一定是G的一条产生式;
(4)若某一结点n至少有一个它自己除外的子孙,并且有标记A,则A一定在非终结符中。
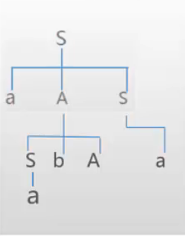
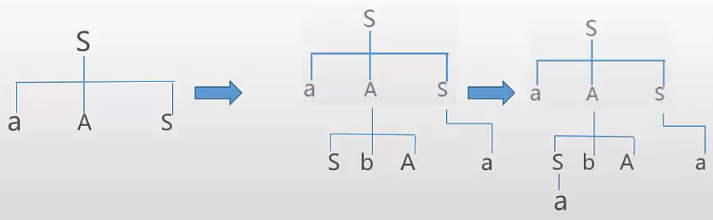
文法G=({a,b},{S,A},S,P),其中:SàaAS|a,AàSbA|SS|ba。请构造句型aabAa的推导树。
解析:
SàaASàa(SbA)Sàa(abA)a
中间代码表达式
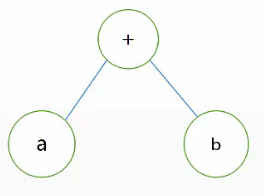
前缀表达式(+ab)
中缀表达式(a+b)
后缀表达式(ab+)
例如,表达式(a-b)*(c+5)的后缀是(D)。
A.abc5+*- B.ab-c+5*
C.abc-*5+ D.ab-c5+*
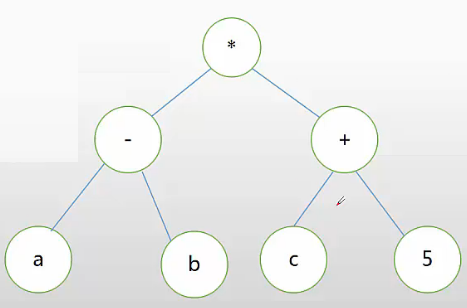
解析:从左至右,从下至上。ab-c5+*