仔细斟酌了几秒钟,我终于决定写下这篇博客,或许应该取一个高大上的名字,比如“Linear Regression to predict PM2.5 using Gradient Descent”,不过回头看了看惨淡的排名…
言归正传,本文仅适合看见该题目无从下手的小白进行参考,用的算法也是入门爆款的线性回归的梯度下降,也是我用py撸的第一个梯度下降,下面切入正题。
题目链接:https://www.kaggle.com/c/ml2019spring-hw1/overview
train.csv因为中文乱码所以我手动把乱码(标题)改成了英文,然后把代表地区的那一列删掉了,因为预测的都是这个地区,这一列没啥用。
首先,看到该题目,我有很多设想,题目说:给定一个月前20天每个小时的PM2.5的值(当然还有别的参数),然后在一个月最后十天里,每十小时为一组,给出前9个小时,预测第10个小时的PM2.5值。
那么我首先就设想,那我把每个小时都单独拎出来进行回归,比如:1月1号的1点,1月2号的1点,1月3号的一点等等,可是问题来了,即便我以这种方式把每一天的每一个小时的PM2.5单独求出一个回归方程,那我如何预测后一天的PM2.5呢?-_-|| 然后这个方法就被我pass掉了。而且事实上,我通过绘图分析,这个方法似乎也不太好。
下图就是我分析的每天0点的的PM2.5值,可以看出每天同一时刻的PM2.5值差别都挺大的。

然后我接着想,PM2.5是每个小时测的,那么理论上每两个相邻间隔下的PM2.5应该差别不会太大,那可不可以把每个小时的PM2.5都做到一个回归里,即不考虑哪天是哪天,而只以小时进行考虑,尽管这种方式跟上面的思路存在同样的问题(即我即便将该回归方程拟合了出来,我又该怎么预测下一时刻的PM2.5值呢?)我还是对前几天的每个小时的PM2.5的图像进行了分析
代码如下,我分析了前10天每天的每个小时的PM2.5的变化趋势

限于篇幅,这里只粘贴前3天的数据,可以看出每天PM2.5的波动还是有一定规律的



尽管每天的PM2.5值的变化有规律,但是最后提供的预测数据是以10个小时为一个单位的,而且上图中也可以看出,相邻小时内PM2.5的值变化可能会很大,比如上午时分上报高峰期时,PM2.5激增。
说了这么多,也没想出什么能用的思路来,那就先直接来最简单粗暴的,我同样把所有数据以10小时为单位分割,用前9小时来预测第10小时,不过为了增加数据量,我采取了一点小策略,下面打个比方:
假设一共测试了12个小时,那么我的数据是:1~ 10小时,2~ 11小时,3~ 12小时,如此如此这般这般,也算是尽可能增加数据量了(但是我并不确定这样更好,或许这就是使结果偏离正确答案的一个重大因素,因为它尽可能将这个思路的效果发挥到了极致,但这个思路或许(事实上也是)本身就有问题)
说这个思路有问题,是因为接下来我采用的就是非常常规的线性回归了,hypothesis就是下图所示了,但这玩意模拟出来的是直线啊,尽管它有10维,但该是直线还是直线,所以它本身就存在一些问题,不过谁叫它最简单呢,现在最重要的是先做出来嘛,做出来了再讲后续优化。
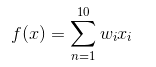
下面以代码为主了。
首先导入一些工具库
# initialize
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
然后导入数据,最下面一行打印出测试数据的维数,结果是(240,23),测试数据量确实挺少的
train_data_path = './train.csv'
test_data_path = './test.csv'
train_data = pd.read_csv(train_data_path)
#这里是把不需要的值给去掉,只留下数据
train_data = train_data[(train_data['kind'] == 'PM2.5')].iloc[:, 3:].astype(int)
train_data.shape
上面的train_data经过处理后结构如下:

下面就是初始化一些值,trainX和trainY就是上面讲的思路将每10组数据都给抽取出来,而且因为用上面的思路给扩充了训练集的大小,因此此时trainX一共有5000多行了
trainX = []
trainY = []
wholeVector = []
# 该循环将训练集中所有数据全部存到一个一维的列表wholeVector中以方便后续操作
for i in range(train_data.shape[0]):
temp = train_data.iloc[i].values
for j in range(len(temp)):
wholeVector.append(temp[j])
for i in range(len(wholeVector) - 9):
tempx = wholeVector[i: i + 9]
tempy = wholeVector[i + 9]
trainX.append(tempx)
trainY.append(tempy)
# 测试集
trainX = np.array(trainX)
# 给trainX的第一列前加入一列全1的列,方便后续矩阵操作(不理解的可以去看看吴恩达的视频)
trainX = np.c_[np.ones(trainX.shape[0]), trainX]
trainY = np.array(trainY)
定义计算损失值的函数,并将损失值保存下来,用来判断算法执行情况,也可以判断learning rate选择的好不好
def getLossValue(X, Y, theta, loss_history):
'''
计算损失值,并将损失值存入loss_history列表中
'''
tempvec = Y - (theta.T.dot(X.T)).T
loss = tempvec.T.dot(tempvec)
loss_history.append(loss)
return loss
下面就正式开始进行模型的训练了,毕竟很简单,关键代码就两三行
# 学习率
learning_rate = 0.00000001
# 参数
theta = np.zeros(10)
# 损失函数的历史取值
loss_history = []
X = trainX
Y = trainY
for i in range(100000):
# 梯度下降前先计算并保存一下损失值,以便之后审查
getLossValue(trainX, trainY, theta, loss_history)
# 更新参数
tempV = (Y - (theta.T.dot(X.T)).T).T.dot(X)
temp2 = -2 * tempV
theta = theta - learning_rate * temp2
print(loss_history)
然后这里最后是打印了loss_history的,即所有的损失值记录

可以看到一开始的损失值高达400余万,还是蛮吓人的,而最后收敛到也有20多万

这么看毕竟不直观,因此我把损失值画了个图,可以看出收敛的还挺快的,看起来似乎迭代一两千次就差不多收敛了,而后迭代十万次百万次得到的结果也不会好太多,因此在这个思路上这个方法似乎已经达到极限了。

损失值从400多万降到20多万,虽然还是蛮高的,不过也是降低了不少了,那就准备提交一下试试。
# 开始预测
test_dataa = pd.read_csv(test_data_path)
test_data = test_dataa[test_dataa['AMB_TEMP'] == 'PM2.5'].iloc[:, 2:].astype(int)
test_result = []
for i in range(test_data.shape[0]):
t = test_data.iloc[i].values
t = np.r_[1, t]
temp = theta.T.dot(t)
if temp < 0:
temp = 0
test_result.append(temp)
test_result中发现了一个负数,当然只比0小了一点点,这是不允许出现的,所以我直接让它等于0了,别的看起来还挺正常的,没有损失值那么吓人。

然后导出数据(PS:因为对pandas不熟悉所以最终还是决定写了个循环):
df = pd.DataFrame([])
for i in range(len(test_result)):
tp = {'id': 'id_' + str(i), 'value': test_result[i]}
tp = pd.DataFrame(tp, index=[i])
df = df.append(tp)
print(df)
output = pd.DataFrame(df)
output.to_csv('submission.csv', index=False)
然后赶紧在kaggle提交一下(注:上传不了文档的需要科学上网哦):

这个得分啥水平呢?
一打开排行榜就是Private Leaderboard,这个得分在这个榜上似乎是相当不错了(一阵窃喜)

咦,旁边还有个Public Leaderboard,点开看看,然后一直滑到最下面

倒数第七啊哈哈哈…

这个比赛因为已经结束了所以上不了榜,咱也不知道这个成绩该上哪个榜,不过我估摸着,还是Public这个吧…
总之,到这儿也算是把代码撸出来了,这个算法也算是为了梯度下降而去下降,并没有从多个方面进行考虑,因此,我在最后还想提出一些优化思想。
1、 是否可以借鉴随机森林的思想(只是说的高大上一点,其实就是取多组值进行预测然后求平均值)?
2、 这条线不应该是直线,而应该是曲线,所以是否可以考虑引入X的平方或者更高次方?
3、 本算法中为了增加测试数据而增加的测试数据是否将本算法本就不太准的准星带的更偏?
4、 最后的预测值能否与时间挂钩,即对于每一个小时都设计一个梯度下降,比如每天的10点,都用当天1~ 9点的数据进行训练,然后需要预测的时间如果是10点就采用这个模型
5、 本题中除PM2.5外还提供了许多别的参数,能否将另外一些参数也考虑在内?
以后或许会有更新…
结语:搞机器学习,数学很重要!而且还得熟练掌握基础的数据分析技巧…