图Graph
作者:尹正杰
版权声明:原创作品,谢绝转载!否则将追究法律责任。
一.图的概述
1>.什么是图
经典定义:图Graph由顶点和边组成,顶点的有穷非空集合为V,边的集合为E,记作 G(V, E) 。 顶点Vertex,数据元素的集合,顶点的集合,有穷非空; 边Edge,数据元素关系的集合,顶点关系的集合,可以为空。
边可以有方向。 无向边记作(A,B) 或者 (B,A) ,使用小括号。 有向边记作<A,B> ,即从顶点A指向顶点B。 <B,A> 表示顶点B指向顶点A。使用尖括号。
有向边也叫做弧,边表示为弧尾指向弧头。
2>.无向图
Undirected Graph
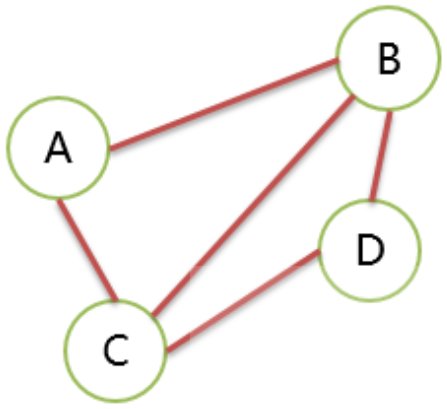
无方向的边构成的图。 G=(V,E) V={A,B,C,D} E={(A,B),(A,C),(B,C),(B,D),(C,D)}

3>.有向图
Directed Graph
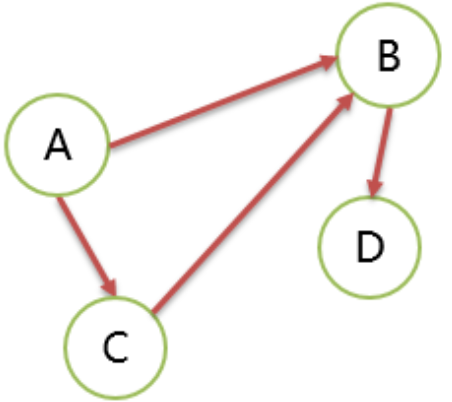
有方向的边构成的图。 G=(V,E) V={A,B,C,D} E={<A,B>,<A,C>,<C,B>,<B,D>}
4>.稀疏图
Sparse Graph
图中边很少。最稀疏的情况,只有顶点没有边,这就是数据结构Set。
5>.稠密图
Dense Graph
图中边很多。最稠密的情况,任意2个顶点之间都有关系。
6>.完全图
Complete Graph 包括了所有可能的边,达到了稠密图最稠密的情况,任意2个顶点之间都有边相连。 有向的边的完全图,叫做有向完全图。边数为n(n-1) 无向的边的完全图,叫做无向完全图。边数为n(n-1)/2 5边形,1+2+3+4,这就是1+2+...+(n-1) = n(n-1)/2

7>.子图
如果图G(V, E)和G'(V', E') 满足V'≤ V 且 E'≤E,则G'是G的子图。
换句话说,就是一个图的部分顶点和部分边组成的图为子图,有向图要注意边的方向。
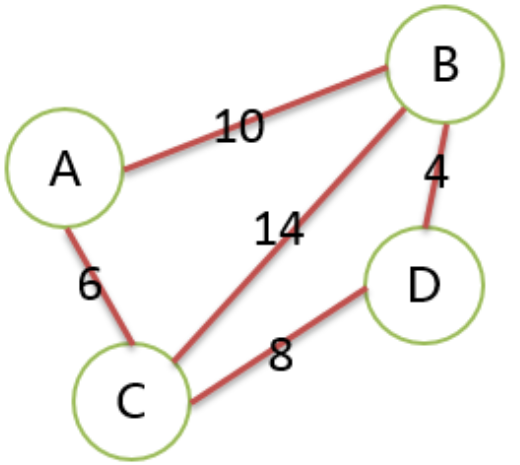
8>.边的权Weight
给边赋予的值称为权。权可以表示距离、所需时间、耗费的时间等。
约定,后面默认说的图,都是不带权的。
9>.网network
图中的边有权,图被称为网
10>.自环Loop
若一条边的两个顶点为同一个顶点,则此边称作自环。
边中存在这样一个边 (u,v) 或者 <u,v> ,且 u=v 。
11>.简单图
无重复的边,或无顶点到自身顶点的边(自环)的图。
我们后面讨论的是简单图的性质。
12>.邻接
图的边集为E。
无向图,若 (u,v)∈ Ε,则称u和v相互邻接,互为邻接顶点。
有向图,若<u,v>∈ Ε,则称u邻接到v,或v邻接于u
简单说,就是2点之间有条边,2点邻接。这说的是点之间的关系。
13>.关联(依附)
若 (u,v) ∈ E 或者 若 <u,v> ∈ E ,则称边依附于顶点u、v ,或 顶点u、v与边相关联。
这说的是点和边的关系。
14>.度Degree
一个顶点的度是指与该顶点相关联的边的条数,顶点v的度记作TD(v)。
无向图顶点的边数叫做度。
有向图的顶点有入度和出度,顶点的度数为入度和出度之和TD(v)=ID(v)+OD(v)。
入度(In-degree):一个顶点的入度是指与其关联的各边之中,以其为终点的边数
出度(Out-degree):出度则是相对的概念,指以该顶点为起点的边数。
15>.路径Path
图G(V,E),其任意一个顶点序列,相邻2个顶点都能找到边或弧依次连接,就说明有路径存在。有向图的弧注意方向。所有顶点都要属于V,所有边都必须属于E。
路径长度
等于顶点数-1,等于此路径上的边数
简单路径 路径上的顶点不重复出现,这样的路径就是简单路径

16>.回路
路径的起点和终点相同,这条路径就是回路。
简单回路
除了路径的起点和终点相同外,其它顶点都不同。
如下图所示:
ABCD就是简单路径。
ACDBA就是简单回路。
ABCDBA是回路,但是不是简单回路。

二.连通
无向图中,顶点间存在路径,则两顶点是连通的。
注意:连通指的是顶点A、D间有路径,而不是说,这两个顶点要邻接。
1>.连通图
无向图中,如果图中任意两个顶点之间都连通,就是连通图。也就是任意2个顶点之间都有路可达。
2>.连通分量
无向图中,指的是“极大连通子图”。
无向图未必是连通图,但是它可以包含连通子图。
3>.强连通
有向图中,顶点间存在2条相反的路径,即从A到B有路径,也存在从B到A的路径,两顶点是强连通的。
下图就没有2个顶点是强连通的。
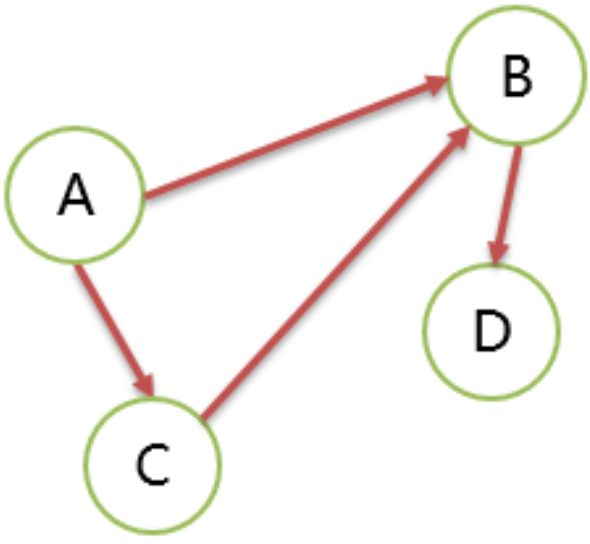
4>.强连通图
有向图中,如果图中任意2个顶点都是强连通,这个图称为强连通图。
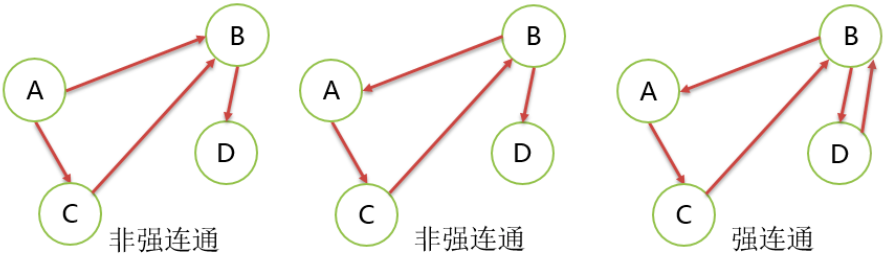
5>.强连通分量
有向图中,指的是“极大强连通子图”。
有向图未必是强连通图,但是可以包含强连通的分量。
三.DAG
一个无环的有向图称做有向无环图(Directed Acyclic Graph),称为DAG。
一个有向图中,任意一个顶点,都找不到一条能回到该顶点的路径。
四.生成树
它是一个极小连通子图,它要包含图的所有n个顶点,但只有足以构成一棵树的n-1条边。 如果一个图有n个顶点,且少于n-1条边,那么一定是非连通图。因为至少要n-1条边才行啊
如果一个图有n个顶点,且多于n-1条边,那么一定有环存在,一定有2个顶点间存在第二条路径。但是不一定是连通图,但是一定有环。
如果一个图有n个顶点,且有n-1条边,但不一定是生成树。要正好等于n-1条边,且这些边足以构 成一棵树
五.有向树
一个有向图恰好有一个入度为0的顶点,其他顶点的入度都为1。注意,这里不关心出度。
生成树森林
若干有向树构成有向树森林
有向无环图不一定能转化为树(因为可能有交叉),但是树一定是有向无环图
六.领接矩阵
图是由vertex和edge组成,所以可以分成2个数组表示。
顶点用一维数组表示,例如v0、v1、v2、v3。
边使用二维数组表示,由顶点构成的二维数组
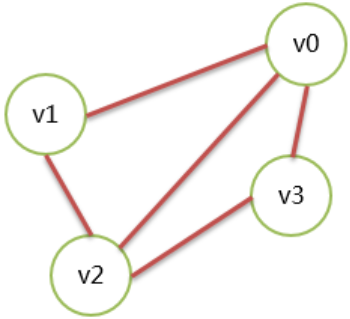
无向图表示,如下图所示,有4个顶点的无向图:
|
v0 |
v1 |
v2 |
v3 |
||
|
v0 |
0 |
1 |
1 |
1 |
|
|
v1 |
1 |
0 |
1 |
0 |
v1度数为2,2条边使用了这个顶点 |
|
v2 |
1 |
1 |
0 |
1 |
|
|
v3 |
1 |
0 |
1 |
0 |
如果对角线上数字为1,说明出现了自环。 如果除了对角线全是1,说明没有自环,且是一个无向完全图。 上面的矩阵,称为图的邻接矩阵。 顶点的度数,等于对应的行或者列求和。 邻接点,矩阵中为1的值对应的行与列对应的顶点就是邻接点。 无向图的邻接矩阵是一个对称矩阵。