推荐系统系列（二）：FFM理论与实践

背景

在CTR/CVR预估任务中，除了FM模型[2] 之外，后起之秀FFM（Field-aware Factorization Machine）模型同样表现亮眼。FFM可以看作是FM的升级版，Yuchi Juan于2016年提出该模型，但其诞生是受启于Rendle在2010年发表的另一个模型PITF [3]（FM也是Rendle在2010年发表的），其论文原文 [1] 中写道：

The idea of FFM originates from PITF proposed for recommender systems with personalized tags.

在各种深度推荐模型出来之前，FM/FFM模型在各大推荐相关的竞赛中大放异彩。今天，我们就来好好梳理一下FFM的原理以及如何将理论转化为实践。

分析

1. FFM公式定义

相较于FM模型，FFM模型引入了域（Field）的概念（该想法来源于PITF [3]），可看做是对特征进行分组。例如，对于性别特征而言，通常有两种取值 (female) 、(male) 。对值进行one-hot编码之后性别特征会拆分为两个独立的特征 (x_{female}) 和 (x_{male}) 。显然，这两个特征具有共同的性质：都属于性别。所以可以将这两个特征归在同一个Field下，即有相同的Field编号。不同域的特征之间，往往具有明显的差异性。对比FM中的做法，每个特征有且仅有一个隐向量，在对特征 (x_i) 与其他特征进行交叉时，始终使用同一个隐向量 (V_i) 。 这种无差别式交叉方式，并没有考虑到不同特征之间的共性（同域）与差异性（异域）。

FFM公式化定义如下：

[y = w_0+sum_{i=1}^nw_ix_i+sum_{i=1}^{n-1}sum_{j=i+1}^nlangle V_{i,f_j},V_{j,f_i} angle x_ix_j ag{1} ]

其中 (f) 为域（Field）映射函数，(f_i) 表示为 (x_i) 特征对应的Field编号。

将公式（1）对比FM可以发现，二者之间的差异仅在于二阶交叉对应的隐向量。设数据集中Field的数目为 (F) ，那么对于每个特征 (x_i) 拥有 (F) 个对应的隐向量，分别应用于与不同域特征进行交叉时。设隐向量维度为 (k) ，FFM二阶交叉项参数为 (nkF) 。

2. 求解

由于引入了Field，公式（1）不能像FM那样进行改写，所以FFM模型进行 推断 时的时间复杂度为 (O(kn^2)) 。

为了方便推导各参数的梯度，隐向量表示为 (V_{i,f_j}=(v_{i,f_j}^1,v_{i,f_j}^3,cdots,v_{i,f_j}^k)) 。公式（1）展开：

[y = w_0+sum_{i=1}^nw_ix_i+sum_{i=1}^{n-1}sum_{j=i+1}^nsum_{q=1}^{k}v_{i,f_j}^{q}v_{j,f_i}^{q}x_ix_j ag{2} ]

当参数为 (w_0) 时，(frac{partial{y}}{partial{w_0}}=1) 。

当参数为 (w_i) 时，(frac{partial{y}}{partial{w_i}}=x_i) 。

当参数为 (v_{i,f_j}^q) 时，其他参数视为常量，只考虑公式（2）交叉项。由于Field数量以及映射关系 (f) 取决于数据集，这种情况参数梯度的数学统一表达式稍微复杂点（但当确定 (f) 之后很好计算），所以这里就暂且按下不表。

3. 性能评估

上述小节并未得到统一的参数梯度表达式，但估计模型训练时的时间复杂度，仍需评估更新 (v_{i,f_j}^q) 参数的时间复杂度。尽管没有梯度公式，但可以通过夹逼定理来确定该参数的更新时间复杂度。两种极端情况：1）(F=1) ；2）(F=n) ；参数更新时间复杂度位于二者之间。

1） (F=1) 时，所有特征均属于同一个Field，此时FFM退化为FM。可以将 (f) 暂时省略，公式（2）可以表示为

[egin{align} y ={} & w_0+sum_{i=1}^nw_ix_i+sum_{i=1}^{n-1}sum_{j=i+1}^nsum_{q=1}^{k}v_{i}^{q}v_{j}^{q}x_ix_j otag \ ={} & w_0+sum_{i=1}^nw_ix_i+sum_{i=1}^{n-1}sum_{q=1}^{k}v_i^qsum_{j=i+1}^{n}v_{j}^{q}x_ix_j otag \ end{align} ag{3} ]

有，

[egin{align} frac{partial{y}}{partial{v_{i,f_j}^q}} ={} & frac{partial{y}}{partial{v_{i}^q}} otag \ ={} & sum_{j=i+1}^{n}v_j^qx_ix_j otag \ end{align} ag{4} ]

所以，更新参数 (v_{i,f_j}^q) 所需时间复杂度为 (O(n))。这只是二阶项中 (nkF) 个参数中的其中一个，所以更新二阶项参数总时间复杂度为 (O(kn^2)) 。

2）(F=n) 时，每个特征的Field都不相同。不失一般性，可以设 (f_i=i) ，此时公式（2）可以表示为

[egin{align} y ={} & w_0+sum_{i=1}^nw_ix_i+sum_{i=1}^{n-1}sum_{j=i+1}^nsum_{q=1}^{k}v_{i,j}^{q}v_{j,i}^{q}x_ix_j otag \ end{align} ag{5} ]

有，

[egin{align} frac{partial{y}}{partial{v_{i,f_j}^q}} ={} & frac{partial{y}}{partial{v_{i,j}^q}} otag \ ={} & v_{j,i}^qx_ix_j otag \ end{align} ag{4} ]

所以，更新参数 (v_{i,f_j}^q) 所需时间复杂度为 (O(1))。这只是二阶项中 (nkF) 个参数中的其中一个，所以更新二阶项参数总时间复杂度为 (O(kn^2)) 。

综上，更新二阶项参数所需时间复杂度为 (O(kn^2)) ，因为 (w_0) 与 (w_i) 参数更新时间复杂度为 (O(1)) ，所以FFM训练的时间复杂度为 (O(kn^2)) 。

总结：FFM 训练/推断 时间复杂度都为 (O(kn^2)) 。

4. 优缺点

优点：

• 在高维稀疏性数据集中表现很好。

• 相对FM模型精度更高，特征刻画更精细。

缺点：

• 时间开销大。FFM时间复杂度为 (O(kn^2)) ，FM时间复杂度为 (O(kn)) 。
• 参数多容易过拟合，必须设置正则化方法，以及早停的训练策略。

5. 注意事项

FFM对于数据集的要求 [1]：

• FFMs should be effective for data sets that contain categorical features and are transformed to binary features.
• If the transformed set is not sparse enough, FFMs seem to bring less benefit.
• It is more difficult to apply FFMs on numerical data sets.

1）含有类别特征的数据集，且需要对特征进行二值化处理。

2）越是稀疏的数据集表现效果相较于其他模型更优。

3）FFM比较难应用于纯数值类型的数据集。

数据预处理 [4]：

与FM一样，最好先进行特征归一化，再进行样本归一化。

超参数对于模型的影响 [1]：

首先需要注意的是，FFM的隐向量维度远小于FM的隐向量维度，即 (k_{FFM} ll k_{FM}) 。

1）隐向量维度 (k) 对于模型的影响不大。

2）正则化系数 (lambda) 如果太大，容易导致模型欠拟合，反之，容易过拟合。

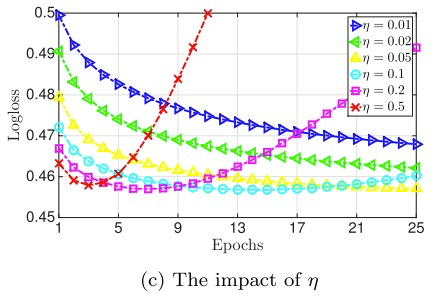
3）在论文中，使用的是Adagrad优化器，全局学习率 (eta) 也是超参数。如果 (eta) 在一个较小的水平，则可以表现最佳。过大，容易导致过拟合。过小，容易欠拟合。

模型训练加速 [1,4]：

1）梯度分布计算；2）自适应学习率；3）多核并行计算；4）SSE3指令并行编程；

实验

与FM一致使用 (MovieLens 100K) 数据集，将评分大于3的样本置为正样本1，其他置为负样本0，构造一个二分类任务。使用 (CrossEntropy) 损失函数，最后使用了 (Adam) 优化算法。

论文中使用的 (logistic loss) 将样本构造为-1、1的二分类，同时使用的是 (Adagrad) 优化算法 [1]

核心代码如下：

class FFM(object):
    def __init__(self, vec_dim, feat_num, field_num, lr, lamda):
        self.vec_dim = vec_dim
        self.feat_num = feat_num
        self.field_num = field_num
        self.lr = lr
        self.lamda = lamda

        self._build_graph()

    def _build_graph(self):
        self.add_input()
        self.inference()

    def add_input(self):
        self.x = tf.placeholder(tf.float32, shape=[None, self.feat_num], name='input_x')
        self.y = tf.placeholder(tf.float32, shape=[None], name='input_y')

    def inference(self):
        with tf.variable_scope('linear_part'):
            w0 = tf.get_variable(name='bias', shape=[1], dtype=tf.float32)
            self.W = tf.get_variable(name='linear_w', shape=[self.feat_num], dtype=tf.float32)
            self.linear_part = w0 + tf.reduce_sum(tf.multiply(self.x, self.W), axis=1)
        with tf.variable_scope('interaction_part'):
            self.V = tf.get_variable(name='interaction_w', shape=[self.feat_num, self.field_num, self.vec_dim], dtype=tf.float32)
            self.interaction_part = tf.constant(0, dtype=tf.float32)
            for i in range(self.feat_num):
                for j in range(i+1, self.feat_num):
                    self.interaction_part += 
                        tf.reduce_sum(tf.multiply(self.V[i, field_map[j]], self.V[j, field_map[i]])) * 
                        tf.multiply(self.x[:, i], self.x[:, j])

        self.y_logits = self.linear_part + self.interaction_part
        self.y_hat = tf.nn.sigmoid(self.y_logits)
        self.pred_label = tf.cast(self.y_hat > 0.5, tf.int32)
        self.loss = -tf.reduce_mean(self.y*tf.log(self.y_hat+1e-8) + (1-self.y)*tf.log(1-self.y_hat+1e-8))
        self.reg_loss = self.lamda*(tf.reduce_mean(tf.nn.l2_loss(self.W)) + tf.reduce_mean(tf.nn.l2_loss(self.V)))
        self.total_loss = self.loss + self.reg_loss

        self.train_op = tf.train.AdamOptimizer(self.lr).minimize(self.total_loss)

感想： FFM 训练速度真的很慢。

reference

[1] Juan, Yuchin, et al. "Field-aware factorization machines for CTR prediction." Proceedings of the 10th ACM Conference on Recommender Systems. ACM, 2016.

[2] Rendle, S. (2010, December). Factorization machines. In 2010 IEEE International Conference on Data Mining (pp. 995-1000). IEEE.

[3] Rendle, Steffen, and Lars Schmidt-Thieme. "Pairwise interaction tensor factorization for personalized tag recommendation." Proceedings of the third ACM international conference on Web search and data mining. ACM, 2010.

[4] https://tech.meituan.com/2016/03/03/deep-understanding-of-ffm-principles-and-practices.html

[5] https://www.jianshu.com/p/781cde3d5f3d

[6] https://zhuanlan.zhihu.com/p/38241764

[7] https://zhuanlan.zhihu.com/p/64113429

[8] https://zhuanlan.zhihu.com/p/50692817

[9] https://blog.csdn.net/leadai/article/details/81713800

知识分享

个人知乎专栏：https://zhuanlan.zhihu.com/c_1164954275573858304

欢迎关注微信公众号：SOTA Lab
专注知识分享，不定期更新计算机、金融类文章