1.题目描述
Description
For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the
same order. One day Farmer John decides to organize a game of Ultimate Frisbee
with some of the cows. To keep things simple, he will take a contiguous range of
cows from the milking lineup to play the game. However, for all the cows to have fun
they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 200,000) potential groups of cows and
their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to
determine the difference in height between the shortest and the tallest cow in the
group.
Input
Line 1: Two space-separated integers, N and Q.
Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i
Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of
cows from A to B inclusive.
Output
Lines 1..Q: Each line contains a single integer that is a response to a reply and
indicates the difference in height between the tallest and shortest cow in the range.
Sample Input
6 3
173425
1 5
4 6
2 2
2.思路
使用线段树进行二分查找。
2.1如何构建一颗线段树?
区间:每一个节点代表一段区间,节点的左右孩子是由节点区间二分形成的两个区间,比当前节点小的区间放到左孩子,比当前节点大的区间放到右孩子。
存值:每一个节点的最大值都保存max(左区间.max,右区间.max).最底层的节点,则就是输入进去的值。
例如,数据如下:a[5]={3,2,5,7,1},他的线段树的构造则如图所示。
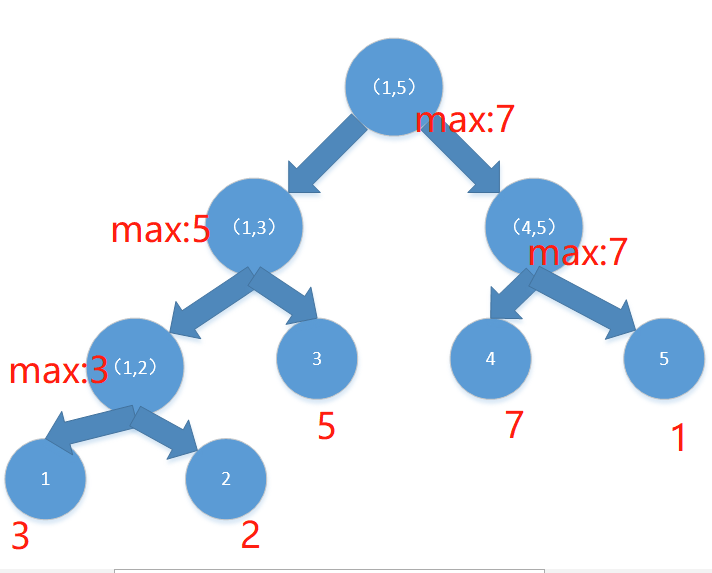
2.2怎么进行查找?
与二分查找类似,在区间中不断进行缩小区域。
3.该题的思路:
3.1构造一颗线段树。除了存进区间值,还需要存进该区间的最大最小值。查找到该段区间的最大最小值之后进行相减,则可以得出答案。
代码实现:

1 #include<iostream> 2 using namespace std; 3 //定义线段树 4 struct node{ 5 int left,right;//描述一段区间 6 int max,min;//分别存放最大值,最小值 7 }tree[100]; 8 9 //建立线段树 10 void Build(int l,int r,int cur){ 11 tree[cur].left=l; 12 tree[cur].right=r; 13 if(l==r){//到达单位区间 14 cin>>tree[cur].max; 15 tree[cur].min=tree[cur].max;; 16 return ; 17 } 18 int mid=(l+r)/2; 19 Build(l,mid,cur*2);//建立左儿子节点 20 Build(mid+1,r,cur*2+1);//建立右儿子节点 21 //存放最大值,最小值 22 if(tree[cur*2].max>tree[cur*2+1].max) 23 tree[cur].max=tree[cur*2].max; 24 else 25 tree[cur].max=tree[cur*2+1].max; 26 27 if(tree[cur*2].min>tree[cur*2+1].min) 28 tree[cur].min=tree[cur*2+1].min; 29 else 30 tree[cur].min=tree[cur*2].min; 31 } 32 //查找一段区间中最大的值 33 int Query1(int l,int r,int cur){ 34 if(l==tree[cur].left&&r==tree[cur].right)///查询区间和节点的区间完全相同 35 return tree[cur].max;///直接返回该节点的最大 36 int mid=(tree[cur].left+tree[cur].right)/2; 37 if(r<=mid)return Query1(l,r,cur*2);///查询区间完全在左儿子节点的区间,则查询左儿子节点 38 else if(l>mid) 39 return Query1(l,r,cur*2+1);///查询区间完全右儿子节点的区间,则查询右子节点 40 else//查询区间在左右儿子节点区间都有,则都查 41 { 42 if(Query1(l,mid,cur*2)>Query1(mid+1,r,cur*2+1)) 43 return Query1(l,mid,cur*2); 44 else return Query1(mid+1,r,cur*2+1); 45 } 46 47 } 48 //查询一段区间内的最小值 49 int Query2(int l,int r,int cur){ 50 if(l==tree[cur].left&&r==tree[cur].right)///查询区间和节点的区间完全相同 51 return tree[cur].min;///直接返回该节点的最小值 52 int mid=(tree[cur].left+tree[cur].right)/2; 53 if(r<=mid) 54 return Query2(l,r,cur*2);///查询区间完全在左儿子节点的区间,则查询左儿子节点 55 else if(l>mid) 56 return Query2(l,r,cur*2+1);///查询区间完全右儿子节点的区间,则查询右子节点 57 else { 58 if(Query2(l,mid,cur*2)>Query2(mid+1,r,cur*2+1)) 59 return Query2(mid+1,r,cur*2+1); 60 else 61 return Query2(l,mid,cur*2); 62 } 63 64 } 65 int main(){ 66 int n,m,l,r; 67 while(cin>>n>>m){ 68 Build(1,n,1); 69 while(m--){ 70 cin>>l>>r; 71 cout<<Query1(l,r,1)-Query2(l,r,1)<<endl;///查询区间[l,r],从根节点1开始 72 } 73 } 74 75 }
4.可不可以用数组来模拟?
开a[n][n]的数组存放区域值。b[n]是原始数据数组
对于1开始的区域,每一段可以用a[1][i]表示1——i的最大值。怎么存放呢,如下:
a[1][1]=b[1];
a[1][2]=max{a[1][1],b[2]};
a[1][3]=max{a[1][2],b[3]};
........................
a[1][i]=max{a[1][i-1],b[i]};
对于2开始的区域同样如此,a[2][i]表示1——i的最大值;
对于第l开始,r结束的区间,a[l][r]直接可以表示区间的最大值。
但是赋值的时候比较麻烦,加上数组真的很大很占内存。
