杭电 1056 HangOver

Problem Description

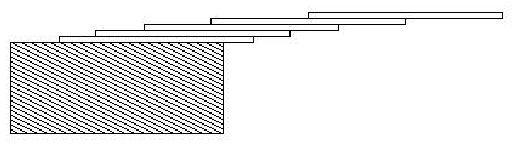
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.



The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

 

Sample Input

1.00 3.71 0.04 5.19 0.00

 

Sample Output

3 card(s) 61 card(s) 1 card(s) 273 card(s)

 

Source

Mid-Central USA 2001

        问题描述：读完英语试题，其实这个题就是给你一个浮点数，一个连续和sum = 1/2+1/3+1/4+1/5+....+1/n;问随着n的增大，sum的增大，sum第一次超过该浮点数时的n值；

　　问题解答：首先建立一个一维数组作查询用，另外注意特殊数据，sum和所给浮点数正好相等时的数据！最后一点我不明白的时，为什么这道题的数据类型一定要是double才能过！

#include <stdio.h>
#include <math.h>
#define MAX 500
#define eps 1e-8

int main()
{
    int i;
    double a[MAX], c;
    for( i = 0; i < MAX; i++ )
        a[i] = 0.0;
    for( i = 1; i < MAX; i++  )
    {
        a[i] = a[i-1] + 1.0 / (i + 1);
    }
    while( (scanf( "%lf", &c ) != EOF)&&( fabs(c) >= eps  ) )
    {
            for( i = 0; i < MAX; i++ )
                if( (a[i] > c)||( fabs(a[i]-c) < eps ) )
                    break;
            printf( "%d card(s)
", i );
    }
    return 0;
}