【洛谷T37388】P哥破解密码

原题图：

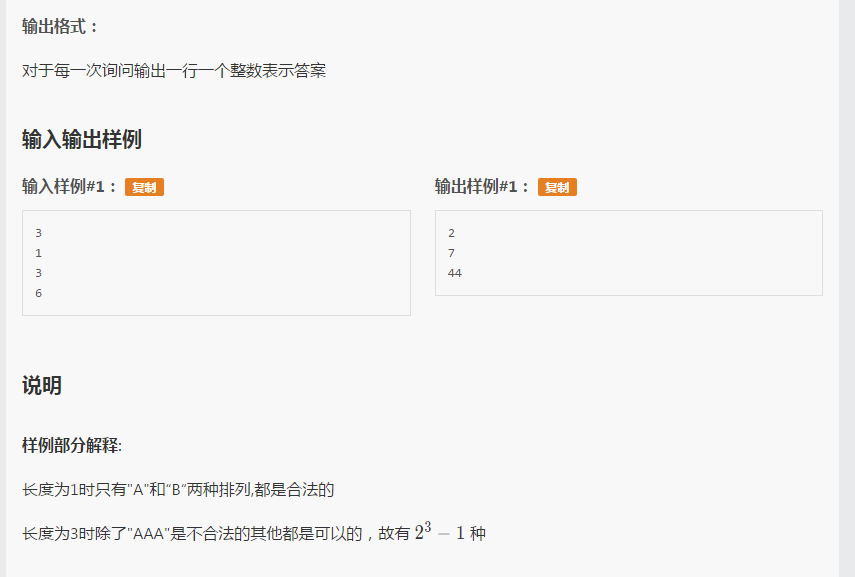
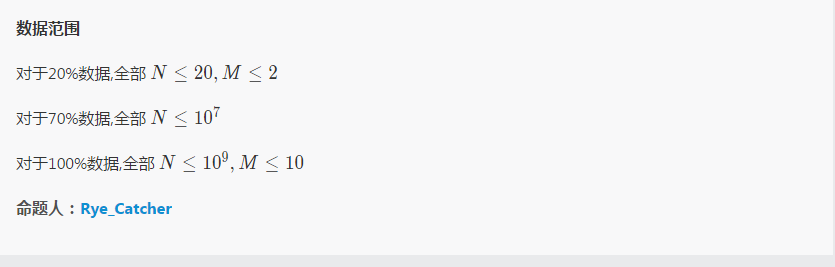
 看到这个题，首先想到的当然是暴力打表找规律了

表：

1　　2

2　　4

3　　7

4　　13

5　　24

6　　44

7　　81

8　　149

9　　274

10　 504

11　 927

12　 1705

13　 3136

14　 5768

15　 10609

发现上下两个数近似于2倍关系，但f[i-1]*2略大于f[i]

用f[i-1]*2-f[i]，发现恰好等于f[i-4]

于是就有了递推式:f[i]=f[i-1]*2-f[i-4]

矩阵加速即可

矩阵加速的方法：

我们有一个4*4的矩阵A和一个向量c[13,7,4,2],

我们要让c*A得到向量c1[13*2-2,13,7,4]

于是得到下面的矩阵：

2  1  0  0
0  0  1  0
0  0  0  1
-1 0  0  0

矩阵快速幂即可

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define MOD 19260817
#define int long long
int T,n,ans[5]={0,2,4,7,13};
struct Matrix{
    int m[5][5];
} O,E,A;
inline Matrix Mul(Matrix X,Matrix Y){
    Matrix Ans=O;
    for(int i=1;i<=4;i++)
     for(int j=1;j<=4;j++)
      for(int k=1;k<=4;k++)
       Ans.m[i][j]=(Ans.m[i][j]+X.m[i][k]*Y.m[k][j])%MOD;
    return Ans;
}
Matrix qpow(Matrix X,int k){
    Matrix S=E;
    while(k){
        if(k&1) S=Mul(S,X);
        k>>=1;
        X=Mul(X,X);
    }
    return S;
}
#undef int
int main()
#define int long long
{
    E.m[1][1]=E.m[2][2]=E.m[3][3]=E.m[4][4]=1;
    A.m[1][1]=2;
    A.m[1][2]=1;
    A.m[2][3]=1;
    A.m[4][1]=-1;
    A.m[3][4]=1;
    scanf("%lld",&T);
    for(int i=1;i<=T;i++){
        scanf("%lld",&n);
        if(n<=4){
            printf("%lld
",ans[n]);
            continue;
        }
        Matrix Ans=qpow(A,n-4);
        int ans=((Ans.m[1][1]*13+Ans.m[2][1]*7+Ans.m[3][1]*4+Ans.m[4][1]*2)%MOD+MOD)%MOD;
        printf("%lld
",ans);
    }
    return 0;
}