目录
1 Filter
1.1 移除低方差特征(Removing features with low variance)
1.2 单变量特征选择 (Univariate feature selection)
1.2.1 卡方检验 (Chi2)
1.2.2 Pearson 相关系数 (Pearson Correlation)
2 Wrapper
2.1 递归特征消除 (Recursive Feature Elimination)
3 Embedding
3.1 使用 SelectFromModel 选择特征 (Feature selection using SelectFromModel)
1 Filter
1.1 移除低方差特征 (Removing features with low variance)
即去掉那些取值变化小的特征
当特征值都是离散型变量的时候这种方法才能用,如果是连续型变量,就需要将连续变量离散化之后才能用。
# Variance 偏差 Threshold阈值 from sklearn.feature_selection import VarianceThreshold X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]] sel = VarianceThreshold(threshold=(.8*(1-.8))) sel.fit_transform(X)

可见,移除了 特征值为 0 的概率达到了 5/6 的第一列。
1.2 单变量特征选择 (Univariate feature selection)
对于分类问题 (y离散),可采用:
-
-
卡方检验
-
对于回归问题 (y连续),可采用:
-
-
皮尔森相关系数 余弦值cos(只考虑了方向)
-
f_regression,
-
mutual_info_regression
-
-
1.2.1 卡方检验 (Chi2)
检验定性自变量对定性因变量的相关性。如 对样本进行一次卡方检验来选择最佳的两项特征:
from sklearn.datasets import load_iris # 鸢尾花数据集 # 用于特征选择的包 from sklearn.feature_selection import SelectKBest # 训练的套路 from sklearn.feature_selection import chi2 iris = load_iris() x, y = iris.data, iris.target # 参数解释:chi2 使用卡方检验,k=2 留下两个特征 x_new = SelectKBest(chi2,k=2).fit_transform(x,y)

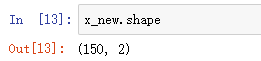
4 个特征只剩 2 个
1.2.2 Pearson 相关系数 (Pearson Correlation)
该方法衡量的是变量之间的线性相关性,结果的取值区间为[-1,1],-1表示完全的负相关,+1表示完全的正相关,0表示没有线性相关。
import numpy as np from scipy.stats import pearsonr # sciPy 科学python哈哈,stats:统计学 np.random.seed(0) # 设置生成随机数的种子 size = 300 x = np.random.normal(0,1,size=size) # 生成标准正态分布的300个数 # Lower noise pearsonr(x, x + np.random.normal(0,1,size)) # Higher noise pearsonr(x, x + np.random.normal(1,10,size))

当噪音比较小的时候,相关性很强,p-value很低。
2. Wrapper
2.1 递归特征消除 (Recursive Feature Elimination)
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,移除若干权值系数的特征,再基于新的特征集进行下一轮训练。
对特征含有权重的预测模型(例如,线性模型对应参数coefficients),RFE (即 一个训练的套路) 通过递归减少考察的特征集规模来选择特征。首先,预测模型在原始特征上训练,每个特征指定一个权重。之后,那些拥有最小绝对值权重的特征被踢出特征集。如此往复递归,直至剩余的特征数量达到所需的特征数量。
from sklearn.feature_selection import RFE from sklearn.ensemble import RandomForestClassifier from sklearn.datasets import load_iris # 建立一个决策树模型 rf = RandomForestClassifier() # 加载鸢尾花数据 iris=load_iris() x, y=iris.data,iris.target # 创建RFE 递归消除特征 # estimator 传入RFE使用到的模型,n_features_to_select 最终剩下几个特征 rfe = RFE(estimator=rf, n_features_to_select=3) x_rfe = rfe.fit_transform(x,y) x_rfe.shape

3 Embedded
3.1 基于L1的特征选择 (L1-based feature selection)
很难指定最终剩几个特征,剩多少算多少哈哈
常用于此目的的稀疏预测模型有 linear_model.Lasso(回归), linear_model.LogisticRegression 和 svm.LinearSVC(分类)
from sklearn.feature_selection import SelectFromModel # 训练套路 from sklearn.svm import LinearSVC # 模型 # penalty 惩罚项,逻辑回归中也有。一般都是默认 l2范数,这里【必须改成 l1】 lsvc = LinearSVC(C=1, penalty='l1', dual=False).fit(x,y) # 进行特征选择,很难预测最后剩几个特征 model = SelectFromModel(lsvc, prefit=True) x_embed = model.transform(x)
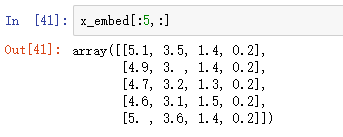
本文只用于学习