感知机-Python实现

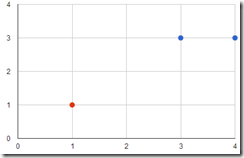
如图3所示的训练数据集，其正实例点是（3，3），（3,4），负实例点是（1,1），试用感知机学习算法的原始形式求感知机模型，即求出w和b。这里，

图3

这里我们取初值，取。具体问题解释不写了，求解的方法就是算法1。

Python代码如下：

 

import os
 
# An example in that book, the training set and parameters' sizes are fixed
training_set = [[(3, 3), 1], [(4, 3), 1], [(1, 1), -1]]
 
w = [0, 0]
b = 0
 
# update parameters using stochastic gradient descent
def update(item):
    global w, b
    w[0] = w[0] + 1 * item[1] * item[0][0]
    w[1] = w[1] + 1 * item[1] * item[0][1]
    b = b + 1 * item[1]
    # print w, b # you can uncomment this line to check the process of stochastic gradient descent
 
# calculate the functional distance between 'item' an the dicision surface
def cal(item):
    global w, b
    res = 0
    for i in range(len(item[0])):
        res += item[0][i] * w[i]
    res += b
    res *= item[1]
    return res
 
# check if the hyperplane can classify the examples correctly
def check():
    flag = False
    for item in training_set:
        if cal(item) <= 0:
            flag = True
            update(item)
    if not flag:
        print "RESULT: w: " + str(w) + " b: "+ str(b)
        os._exit(0)
    flag = False
 
if __name__=="__main__":
    for i in range(1000):
        check()
    print "The training_set is not linear separable. "

运行结果如下：