ARIMA模型原理以及代码实现案例

一、时间序列分析

北京每年每个月旅客的人数，上海飞往北京每年的游客人数等类似这种顾客数、访问量、股价等都是时间序列数据。这些数据会随着时间变化而变化。时间序列数据的特点是数据会随时间的变化而变化。

随机过程的特征值有均值、方差、协方差等。如果随机过程的特征随时间变化而变化，那么数据是非平稳的，相反，如果随机过程的特征随时间变化而不变化，则此过程是平稳的。

如图所示：

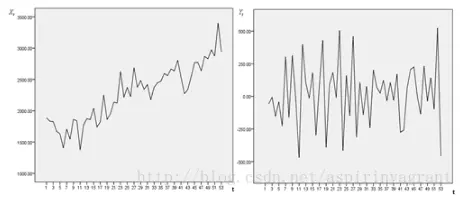
非平稳时间序列分析时，若导致非平稳的原因是确定的，可以用的方法主要有趋势拟合模型、季节调整模型、移动平均、指数平滑等。

若导致非平稳的原因是随机的，方法主要有ARIMA，以及自回归条件异方差模型等。

二、ARIMA

1、简介

ARIMA通常用于需求预测和规划中。可以用来对付随机过程的特征随着时间变化而非固定。并且导致时间序列非平稳的原因是随机而非确定的。不过，如果从一个非平稳的时间序列开始，首先需要做差分，直到得到一个平稳的序列。模型的思想就是从历史的数据中学习到随时间变化的模式，学到了就用这个规律去预测未来。

ARIMA（p，d，q）

• d是差分的步长（差分的阶数指的是进行多少次差分。比如步长为n的一阶差分diff(x) = f(x) - f(x - n)， 而二阶步长为n的差分： diff(x) = f(x) - f(x-n), diff(x-n) = f(x-n) - f(x - n - n), diff_二阶差分(x - n) = diff(x) - diff(x-n)），用来得到平稳序列
• p为相应的自回归项
• q是移动平均项数

2、自回归模型AR

自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性。

自回归模型需要先确定一个阶数p，表示用几期的历史值来预测当前值。p阶自回归模型可以表示为：

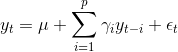
y_t是当前值，u是常数项，p是阶数，r是自相关系数，e是误差

AR的限制：

•  自回归模型是自身的数据进行预测
• 必须具有平稳性
• 必须具有相关性
• 如果自相关系数小雨0.5，则不宜采用
• 自回归只适用于预测与自身前期相关的现象

3、移动平均模型MA

移动平均模型关注的自回归模型中的误差项的累加，q阶自回归过程的公式定义如下：

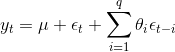
移动平均模型能有效地消除预测中的随机波动

4、自回归移动平均模型ARMA

自回归模型AR和移动平均模型MA模型相结合，我们就得到了自回归移动平均模型ARMA(p,q)，计算公式如下：

5、p、q的确定

　　（1）

　　

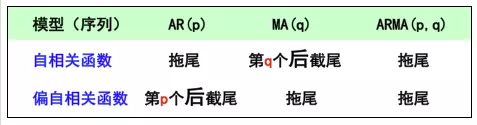
　　（2）结合最终的预测误差来确定p、q的阶数，在相同的预测误差情况下，根据奥斯卡姆剃刀准则，模型越小越好。平衡预测误差和参数个数，我们可以根据信息准则函数法，来确定模型的阶数。预测误差通常用平方误差即残差平方和来表示。

　　　　 常用的信息准则函数法：

• ACI == 2*(模型参数个数)-2ln(模型的极大似然函数)
• BIC = ln(n) * （模型中参数的个数）-2ln(模型的极大似然函数值)，n是样本容量

6、模型的检验

主要的检验值：

• 检验参数估计的显著性（t检验）
• 检验残差序列的随机性，即残差之间是独立的

残差序列的随机性可以通过自相关函数法来检验，即做残差的自相关函数图

三、代码实现

摘自kaggle一道题目。Web traffic。链接：

https://www.kaggle.com/mohitguptaomg/simple-forecast-with-ar-ma-arima

1、背景

维基百科的每一个主题每一天都有一个浏览量。给定了每一个主题历史的浏览数目，让你预测一下未来这个主题浏览数目。

2、 步骤

• 检查数据平稳性
• 使数据平稳
• 对数据求差分
• 求自相关系数和偏相关系数
• 使用ARIMA模型

1、检查数据平稳性并且使数据平稳, 然后对数据求差分

import pandas as pd
import numpy as dragon
import pylab as p
import matplotlib.pyplot as plot
from collections import Counter
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.seasonal import seasonal_decopose
.....
.....
def test_stationarity(x):
    result = adfuller(x)
    print('ADF : %f' % result[0])
    print('p-value: %f' % result[1])
    for key, value in result[4].items():
        if result[0] > value:
            print("The data is non stationery")
        else:
            print("The data is stationery")
        break


tv_log = dragon.log(total_view['en']) # log使数据波动幅度变小，常用处理方法
tv_log_diff = tv_log - tv_log.shift() # 步长为1的差分
tv_log_diff.dropna(inplaces=True)
test_stationarity(tv_log_diff)

2、求自相关系数与便相关系数

from statsmodels.tsa.statools import acf, pacf

lag_acf = acf(tv_log_diff, nlags=10)
lag_pacf = pacf(tv_log_diff, nlags=10, method='ols')

plot.subplot(1, 1, 1)
plot.plot(lag_acf)

plot.axhline(y=0, linestyle='--', color='g')
plot.title('Autocorrelation Function')
plot.show()


plot.subplot(1, 1, 1)
plot.plot(lag_pacf)

plot.axhline(y=0, linestyle='--', color='g')
plot.title('Partial Autocorrelation Function')
plot.show()

结果：

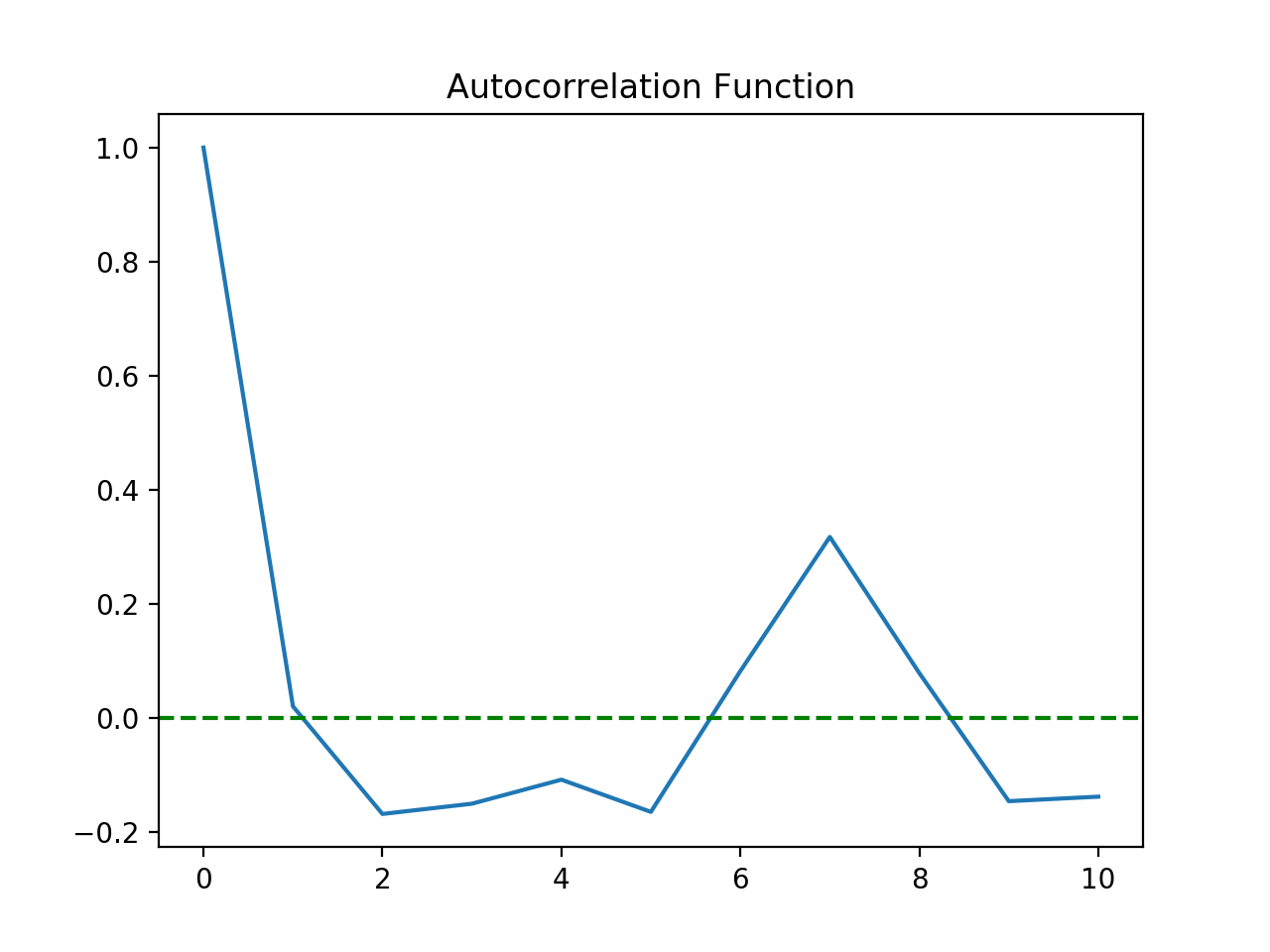
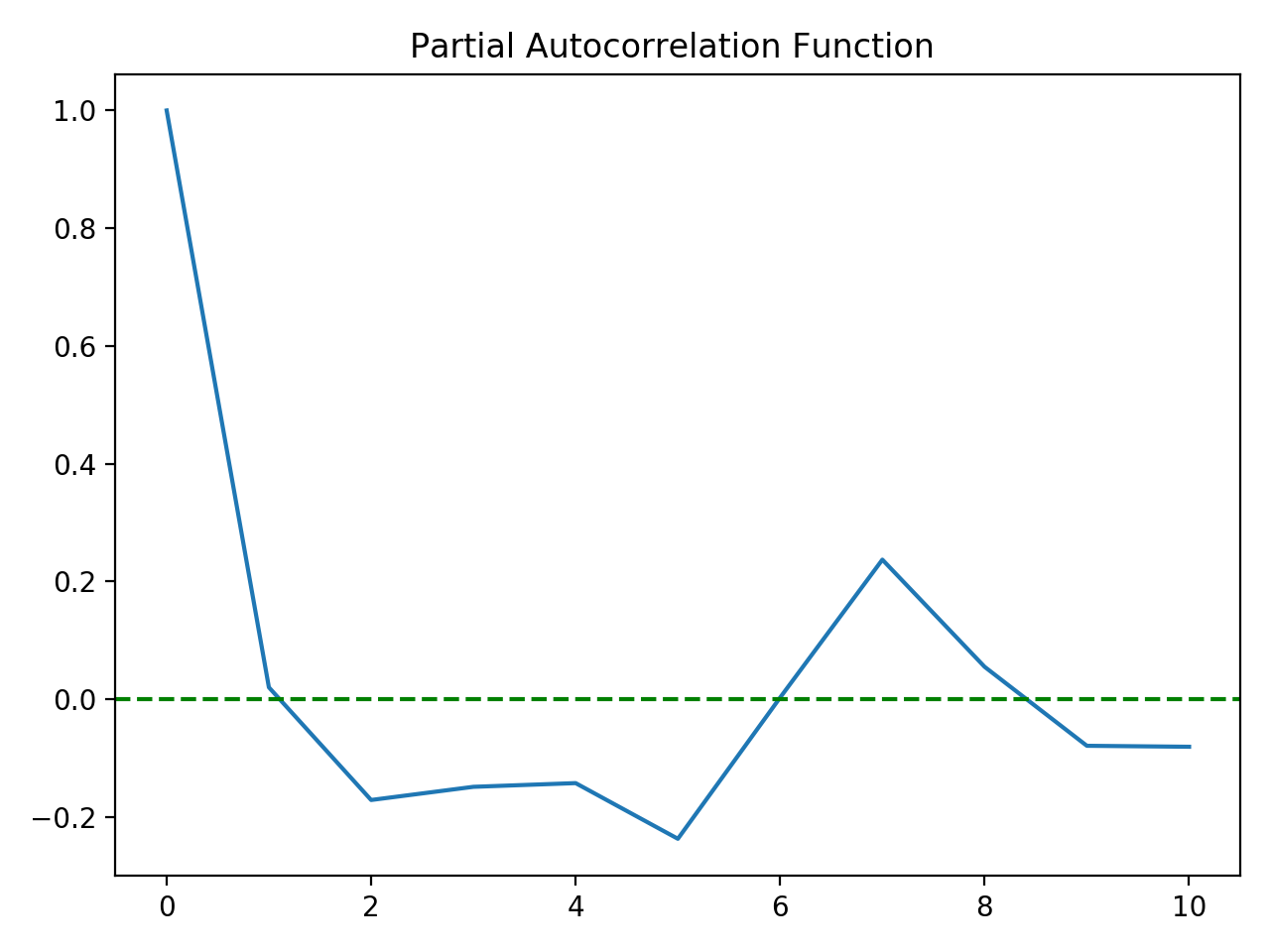
可以看到截尾的位置均为1处，因此p，q均取1.

3、ARIMA

from statsmodels.tsa.arima_model import ARIMA
from pandas import DataFrame

size = int(len(tv_log - 100))
train_arima, test_arima = tv_log[0:size], tv_log[size:len(tv_log)]
history = [x for x in train_arima]
predictions = list()
originals = list()
error_list = list()

for t in range(len(test_arima)):
    # 预测一个重新训练一遍模型
    model = ARIMA(history, order=(1, 1, 1)) # 不要使用差分后的数据， 这里面填写的是步长为d的差分 order对应的参数（p，d, q）
    model_fit = model.fit(disp=0)
    output = model_fit.forcast()
    pred_value = dragon.exp(output[0])
    original_value = dragon.exp(test_arima[0])

    predictions.append(pred_value)
    originals.append(original_value)