SPFA

一、解决问题

从图中的某个顶点出发到达另一个顶点的最短路径。

二、算法思路

Shortest Path Faster Algorithm (SPFA)。一般认为是队列优化的贝尔曼-福特算法。是一个用于求有向带权图单源最短路径的算法，并且适用于有负权重的图。如果一个顶点被加入了超过顶点的个数，则这个图就有负环

基本思路

• 每个节点都用于松弛其相邻节点的备选节点。
• 维护一个备选节点队列
• 仅有节点被松弛后才会放入队列
• 上述流程不断重复直到队列没有节点

伪代码：

function spfa(G, s):
    //初始化所有节点都是最大距离
    for each vertex != s in G:
        d[vertex] = inf
    d[s] = 0
    offer s into queue
    while(queue is not empty):
        u = poll queue
        for each v in edge(u):
            if d[u] + w[u, v] < d[v]:
                d[v] = d[u] + w[u,v]
                if v not in queue:
                    offer v into queue

三、图例

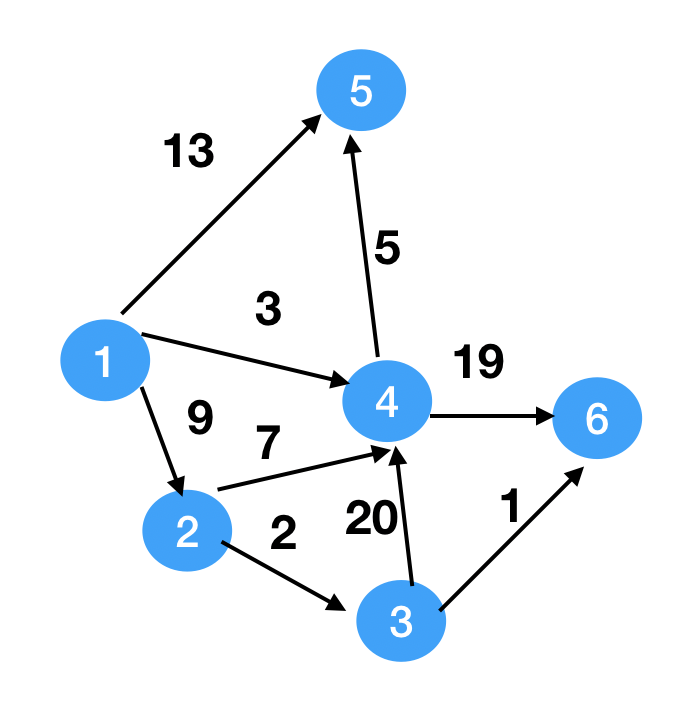
首先算一下最短路径为了用来验证

distance(1,5) = 8
distance(1,4) = 3
distance(1,2) = 9
distance(1,3) = 11
distance(1,6) = 12

过程

• d[a] 为源点到a的距离
• poll为从队列取出点
• offer为每次放入队列的点
• q为队列
• 红色的为最后的结果

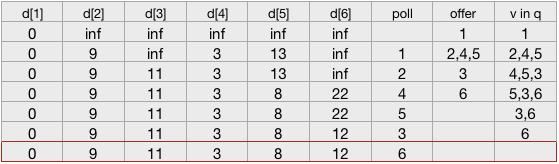
四、 Code (这里面的图表示形式用链式前向星更简洁一些)

package algorithm;


import java.util.*;

public class SPFATest {
    private static final int INF = 0x7fffffff;
    private static class Edge {
        int source;
        int target;
        int weight;

        private Edge(int source, int target, int weight){
            this.source = source;
            this.target = target;
            this.weight = weight;
        }
    }
    public static class Graph {
        

        int[] nodes;
        HashMap<Integer, List<Edge>> nodeWithEdges;

        private Graph init(int[] nodes, List<Edge> edges) {
            this.nodes = nodes;
            nodeWithEdges = new HashMap<>();
            for (Edge edge : edges) {
                List<Edge> edgeTemp = nodeWithEdges.getOrDefault(edge.source, new ArrayList<>());
                edgeTemp.add(edge);
                nodeWithEdges.put(edge.source, edgeTemp);
            }
            return this;
        }

        public int[] getAllNodes() {
            return this.nodes;
        }

        private List<Edge> getEdgesOfNode(int node) {
            return nodeWithEdges.get(node);
        }
    }

    public static int[] SPFA(int source, Graph graph) {
        int n = graph.nodes.length;
        int[] d = new int[n+1];
        for (int i = 0; i <= n; i++) {
            d[i] = INF;
        }
        d[source] = 0;
        boolean[] nodeExistsInQ = new boolean[n+1];
        Deque<Integer> deque = new ArrayDeque<>();
        deque.offer(source);
        nodeExistsInQ[source] = true;

        while (!deque.isEmpty()) {
            int u = deque.poll();
            nodeExistsInQ[u] = false;
            if(graph.getEdgesOfNode(u) == null) continue;

            for (Edge edge : graph.getEdgesOfNode(u)) {
                int v = edge.target;
                if (d[u] + edge.weight < d[v]) {
                    d[v] = edge.weight + d[u];

                    if(!nodeExistsInQ[v]){
                        deque.offer(v);
                        nodeExistsInQ[u] = true;
                    }
                }
            }
        }
        return d;
    }

    public static void main(String [] args){
        int []nodes = new int[]{1,2,3,4,5,6};
        List<Edge> edges = new ArrayList<>();
        edges.add(new Edge(1,2,9));
        edges.add(new Edge(1,4,3));
        edges.add(new Edge(1,5,13));
        edges.add(new Edge(2,4,7));
        edges.add(new Edge(2,3,2));
        edges.add(new Edge(3,4,20));
        edges.add(new Edge(3,6,1));
        edges.add(new Edge(4,5,5));
        edges.add(new Edge(4,6,19));

        Graph graph = new Graph().init(nodes, edges);

        int []d = SPFA(1, graph);
        for(int i = 1; i <= nodes.length; i++){
            System.out.println(d[i]);
        }
    }
}