行人检测中的mr，fppi这些指标？？？
3种距离：欧式距离、SmoothL1距离、IoU距离
总的loss公式：3个部分组成Lattr是预测框和匹配的gt尽可能接近
Lrepgt是预测框和周围没匹配的gt尽可能远离
Lrepbox是预测框和周围的其他预测框尽可能远离
整体上loss的计算是针对每个正样本的预测框
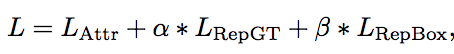
1.Lattr：
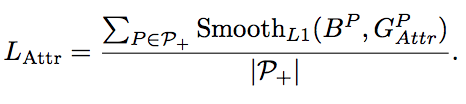
p+是所有的正样本proposal的集合，Lattr是为了公平的对比，依旧采用了smoothL1。
为什么Lattr是让预测框和匹配的gt尽可能接近？
smoothl1的公式如下图：
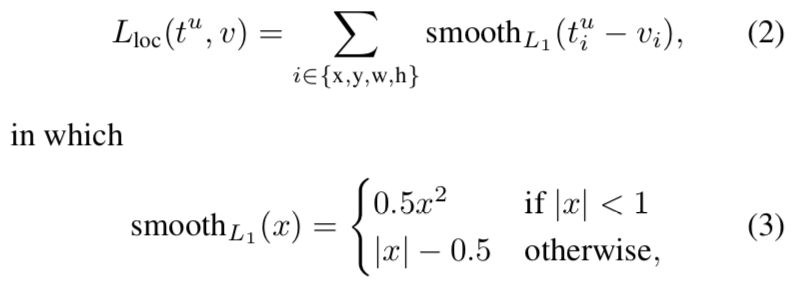
从公式可以看出，是预测框和gt的x、y、w、h分别进行smoothl1计算然后累加和，优化的目标其实是让这些值的差值更小，既然差值更小，两个框就越相同，即越靠近。
2.Lrepgt：
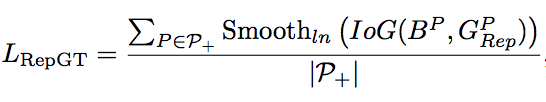
Lrepgt中G的公式如下：
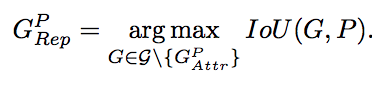
也就是说G是除了与预测框匹配的gt以外所有其他剩下的gt中与预测框iou最大的gt
Lrepgt采用的smoothLn和iog
为什么使用iog、iou+smoothLn，而不使用smoothl1？
原论文中说：smoothl1是让预测框和遮挡的gt越来越远，但iog、iou+smoothLn是缩小两者的交集，更符合motivation
为什么采用iog，而不使用iou?
首先明确gt框的大小和位置是不变的，如果使用iou，可能会通过放大预测框的方式来降低loss，也就是通过增大并集，iou的分母部分(当然这种情况也可能分子也会增加，但最大的可能是分子的增加赶不上分母的增加)；使用iog，就只能优化分子部分，也就是两个框的交集部分，这也是作者的目的(当然最想要的是预测框远离另一个gt，但也可能通过缩小预测框达到这个目的，不过总比iou这种好)。总的来说，iou会比iog多一个优化的变量，让可能的优化的目标走偏，并且iog更符合作者的motivation
3.Lrepbox：
这个loss的目的是使预测框远离相邻不是预测同一真实目标的预测框。首先根据真实目标框GT将P_+分为不同的子集，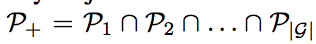
，然后使得来自与不同子集的proposal的overlap尽可能的小。分母中的示性函数，其实就是iou大于0就直接输出结果，iou等于0就输出0，表示的意思是：必须是有交集的预测框才计入损失值，如果两个proposal完全不相邻，则不计入。
这个为什么能解决nms的问题？？？
为什么Lrepgt是让预测框与其他gt框远离？为什么Lrepbox是让预测框和周围的其他预测框尽可能远离？
Lrepgt优化的是iog，iog的分子是交集，分母是两个框的和。如果你只使用交集来优化，那可以通过缩小框的大小来减小交集。但是采用的是iog，gt肯定是保持不变的，一般情况下分母也是不变的，那样就只能去减小分子，即两个的交集，这样就远离。
Lrepbox采用iou，其实两个框都是可以变化的。
smooth-ln的公式如下图：
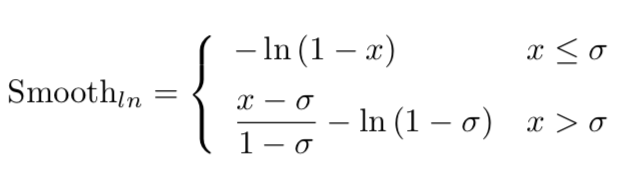
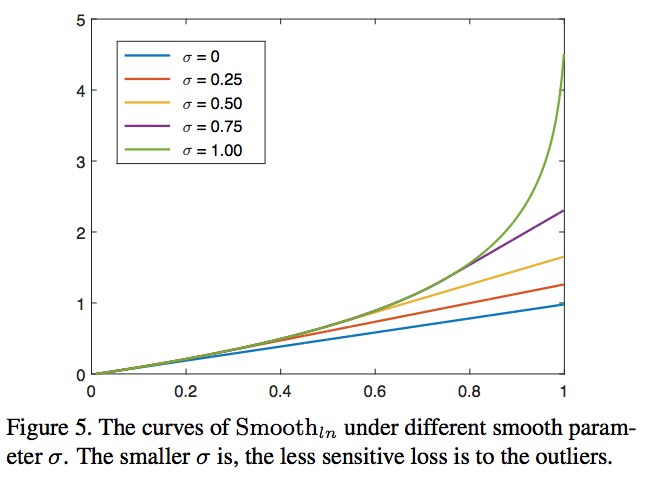
delta越小，对异常值就越不敏感。iou或者iog的取值在[0,1]之间，一般来说1这种就算异常值了，可以看到delta越小，取值就越小，并且相对于其他值变化不是那么大，这样就越不敏感了。
这其实类似于smoothl1跟l2-loss的对比关系，smoothl1相对于l2-loss对异常值更加不敏感。
正如Smooth_l1不会对特别大的偏差给予过大的penalty，Smooth_ln对于很小接近于1的输入也不会像原始的ln函数一样给予负无穷那么大的loss，从而可以稳定训练过程，而且对抗一些outlier。
RepBox相对于RepGT有更多的outliers，所以应该弱化其对σ的敏感性，论文实验中RepGT和RepBox分别在σ=1和σ=0取得更好的效果。
当delta为1时，就跟iou-loss一样，-ln(1-IoG) （unitbox）
https://zhuanlan.zhihu.com/p/43655912
https://www.zhihu.com/search?type=content&q=repulsion%20loss
https://blog.csdn.net/weixin_42615068/article/details/82391354
repulsion-loss的一个实现：https://github.com/JegernOUTT/repulsion_loss/blob/master/repulsion_loss.py