题目传传传送门:http://codeforces.com/contest/1028/problem/C
C. Rectangles
You are given nn rectangles on a plane with coordinates of their bottom left and upper right points. Some (n−1)(n−1) of the given nn rectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.
Find any point with integer coordinates that belongs to at least (n−1)(n−1) given rectangles.
Input
The first line contains a single integer nn (2≤n≤1326742≤n≤132674) — the number of given rectangles.
Each the next nn lines contains four integers x1x1, y1y1, x2x2 and y2y2 (−109≤x1<x2≤109−109≤x1<x2≤109, −109≤y1<y2≤109−109≤y1<y2≤109) — the coordinates of the bottom left and upper right corners of a rectangle.
Output
Print two integers xx and yy — the coordinates of any point that belongs to at least (n−1)(n−1) given rectangles.
Examples
3
0 0 1 1
1 1 2 2
3 0 4 1
1 1
3
0 0 1 1
0 1 1 2
1 0 2 1
1 1
4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4
1 1
5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2
3 4
The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.
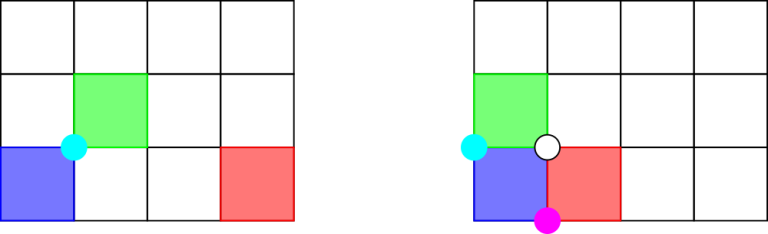
The picture below shows the rectangles in the third and fourth samples.
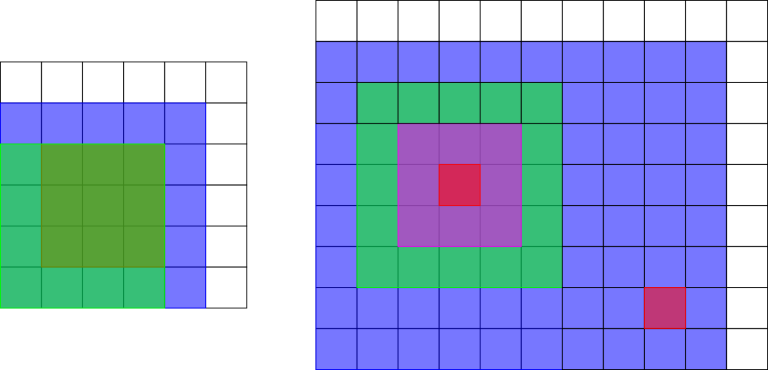
题意概括:
N个矩阵,每个矩阵的表示方法是给左下角和右上角的坐标,求一个点至少在(N-1)个矩阵内部,求这个点的坐标(如果有多个输出其中一个就可以了)。
解题思路:
比赛时TLE的思路是二维树状数组标记,然后查询找被标记了至少(N-1)次的点。
TLE code:

1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 #include <cstring> 5 #include <cmath> 6 #include <map> 7 #define ll long long int; 8 #define INF 0x3f3f3f3f 9 using namespace std; 10 const int MAXN = 132648; 11 const int MAX = 1e9; 12 int x[MAXN], y[MAXN]; 13 map<int,map<int, int> >mmp; 14 int N, T; 15 16 int lowbit(int x) 17 { 18 return x&(-x); 19 } 20 21 void add(int x, int y, int value) 22 { 23 for(int i = x; i <= MAX; i += lowbit(i)) 24 for(int j = y; j <= MAX; j += lowbit(j)) 25 mmp[i][j] += value; 26 } 27 28 int sum(int x, int y) 29 { 30 int res = 0; 31 for(int i = x; i > 0; i -= lowbit(i)) 32 for(int j = y; j > 0; j -= lowbit(j)) 33 res+=mmp[i][j]; 34 return res; 35 } 36 37 void init() 38 { 39 for(int i = 0; i <= N; i++) 40 for(int j = 0; j <= N; j++) 41 mmp[i][j] = 0; 42 } 43 44 int main() 45 { 46 int x1, y1, x2, y2; 47 scanf("%d", &N); 48 for(int i = 1; i <= N; i++) 49 { 50 scanf("%d %d %d %d", &x1, &y1, &x2, &y2); 51 x1++, x2++, y1++, y2++; 52 x[i] = x1; 53 y[i] = y1; 54 add(x1, y1, 1); 55 add(x2+1, y1, -1); 56 add(x1, y2+1, -1); 57 add(x2+1, y2+1, -1); 58 } 59 for(int i = 1; i <= N; i++) 60 { 61 if(sum(x[i], y[i]) >= N-1) 62 { 63 printf("%d %d", x[i]-1, y[i]-1); 64 break; 65 } 66 } 67 return 0; 68 }
然而这道题其实是道YY题...求矩阵前缀交集和后缀交集,然后 O(n) 枚举每一个点不在交集中的情况(也就是该点前缀交后缀的情况),如果该点不在时存在合法交集,那么答案就出来了。
AC code:

1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define LL long long int 4 using namespace std; 5 const int MAXN = 150000; 6 typedef struct Date{ 7 int x1, x2, y1, y2; 8 }; 9 Date P[MAXN], st[MAXN], ed[MAXN]; 10 int N; 11 12 inline Date add(Date a, Date b) 13 { 14 Date res; 15 res.x1 = max(a.x1, b.x1); 16 res.y1 = max(a.y1, b.y1); 17 res.x2 = min(a.x2, b.x2); 18 res.y2 = min(a.y2, b.y2); 19 return res; 20 } 21 22 int main() 23 { 24 scanf("%d", &N); 25 for(int i = 1; i <= N; i++) 26 { 27 scanf("%d%d%d%d", &P[i].x1, &P[i].y1, &P[i].x2, &P[i].y2); 28 } 29 st[1] = P[1]; ed[N] = P[N]; 30 for(int i = 2; i <= N; i++) st[i] = add(st[i-1], P[i]); 31 for(int i = N-1; i >= 1; i--) ed[i] = add(ed[i+1], P[i]); 32 33 for(int i = 1; i <= N; i++){ 34 Date cur; 35 if(i == 1) cur = ed[2]; 36 else if(i == N) cur = st[N-1]; 37 else cur = add(st[i-1], ed[i+1]); 38 if(cur.x1 <= cur.x2 && cur.y1 <= cur.y2){ 39 printf("%d %d ", cur.x1, cur.y1); 40 break; 41 } 42 } 43 return 0; 44 }
