数值分析实验之矩阵的LU分解及在解线性方程组中的应用（Python 代码）

一、实验目的

  1． 借助矩阵理论进一步对消去法作分析，建立高斯消去法与矩阵因式分解的关系。

  2． 会矩阵的紧凑格式的LU分解法、对称阵的分解法。

  3． 会直接三角分解法线性方程组；会选列主元三角分解法解线性方程组。

  4. 将第2个程序改为选列主元三角分解法解方程组的程序。

二、实验原理

     Gauss-Jordan消元法;初等变换。

三、实验程序

     

四、实验内容

  1． 求如下4阶矩阵的LU分解。

        

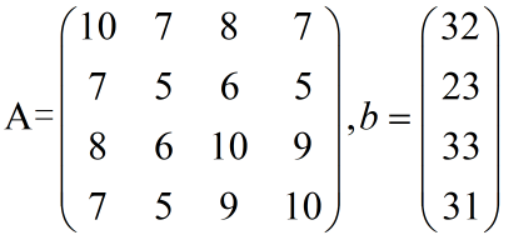
   2． 用直接三角分解法，求一个4元线性方程组的解。

五、实验程序

   • LU分解

from numpy import*

def decA(A):
    A=array(A)
    n=len(A)
    L=zeros((n,n))
    U=zeros((n,n))
    U[0,:]=A[0,:]
    L[:,0]=A[:,0]/U[0,0]
    for i in range(n):
        L[i,i]=1
    for row in range(n-1):
        flag=1
        for col in range(row,n-1):
            U[row+1,col+1]=A[row+1,col+1]-dot(L[row+1,:],U[:,col+1])#计算U矩阵非零元素
            if (row+2<n)&(flag==1):#计算L矩阵非零元素
                for k in range(1,row+2):
                    L[row+2,k]=(A[row+2,k]-dot(L[row+2,:],U[:,k]))/U[k,k]
            flag+=1
    print("U = ",U)
    print("L = ",L)
    
def main():
    A=[[10, 7, 8, 7],
       [7, 5, 6, 5],
       [8, 6, 10, 9],
       [7, 5, 9, 10]]
    decA(A)
main()

    运行结果：

         

• 直接三角分解法

import numpy as np

input001= list(map(int, input().split()))
n = int(input001[0])

a = np.zeros((n,n),dtype = np.double)
for r in range(n):
    a[r,:] = np.array(input().split(),dtype = np.double)

b = np.zeros((n,1),dtype= np.double)
for r in range(n):
    b[r] = np.array(input(),dtype=np.double)


for i in range(n):
    max = i#换行标记符
    for i1 in range(i,n):
        if(a[max][i]<a[i1][i]):
            max = i1
    if(max == i):
        for k in range(i,n-1):
            x = a[k+1][i]/a[i][i]
            a[k+1][i] = x
            for m in range (i+1,n):
                a[k+1][m] = a[k+1][m] - x*a[i][m]
    else:
        for i2 in range (i,n):
            temp = a[i][i2]
            a[i][i2] = a[max][i2]
            a[max][i2] = temp
        temp = b[max][0]
        b[max][0] = b[i][0]
        b[i][0] = temp
        for i3 in range(0,i):
            temp = a[i][i3]
            a[i][i3] = a[max][i3]
            a[max][i3] = temp
        for k in range(i,n-1):
            x = a[k+1][i]/a[i][i]
            #a1[k+1][i] = x
            a[k+1][i] = x
            for m in range (i+1,n):
                a[k+1][m] = a[k+1][m] - x*a[i][m]
print(a)


for i in range (1,n):
    x = 0
    for i1 in range (0,i):
        x = a[i][i1]*b[i1][0] + x
    b[i] = (b[i][0] - x)

b[n-1][0] = b[n-1][0]/a[n-1][n-1]
for i in range(n-2,-1,-1):
    x = 0
    for i1 in range (i,n-1):
        x = x + a[i][i1+1]*b[i1+1][0]
    b[i][0] = (b[i][0]-x)/a[i][i]
print(b)

      运行结果：

        

• 矩阵的三角分解要求矩阵的各阶顺序主子式均不为零，故在程序中加入对矩阵顺序主子式的判别，再进行LU分解

import numpy as np
import pandas as pd
 
#np.random.seed(2)
def det(A):     #求A的行列式
    if len(A) <= 0:
        return None
    elif len(A) == 1:
        return A[0][0]
    else:
        s = 0
        for i in range(len(A)):
            n = [[row[a] for a in range(len(A)) if a != i] for row in A[1:]]  # 这里生成余子式
            s += A[0][i] * det(n) * (-1) ** (i )
        return s
 
def Master_Sequential(A,n):   #判断A的k阶顺序主子式是否非零，非零满足LU分解的条件
    for i in range(0,n):
        Master = np.zeros([i+1,i+1])
        for row in range(0,i+1):
            for a in range(0,i+1):
                Master[row][a]=A[row][a]
        if det(Master)==0:
            done=False
            return done
 
 
def LU_decomposition(A):
    n=len(A[0])
    L = np.zeros([n,n])
    U = np.zeros([n, n])
    for i in range(n):
        L[i][i]=1
        if i==0:
            U[0][0] = A[0][0]
            for j in range(1,n):
                U[0][j]=A[0][j]
                L[j][0]=A[j][0]/U[0][0]
        else:
                for j in range(i, n):#U
                    temp=0
                    for k in range(0, i):
                        temp = temp+L[i][k] * U[k][j]
                    U[i][j]=A[i][j]-temp
                for j in range(i+1, n):#L
                    temp = 0
                    for k in range(0, i ):
                        temp = temp + L[j][k] * U[k][i]
                    L[j][i] = (A[j][i] - temp)/U[i][i]
    return L,U
 
if __name__ == '__main__':
    n=3
    A=[[10, 7, 8, 7],
       [7, 5, 6, 5],
       [8, 6, 10, 9],
       [7, 5, 9, 10]]
    print('A矩阵：
',A)
    if Master_Sequential(A,n) != False:
        L,U=LU_decomposition(A)
        print('L矩阵：
',L, '
U矩阵：
',U)
    else:
        print('A的k阶主子式不全非零，不满足LU分解条件。')

    运行结果：

        

• 平方根法

import numpy as np
A=[[10, 7, 8, 7],
       [7, 5, 6, 5],
       [8, 6, 10, 9],
       [7, 5, 9, 10]]
b=[[32, 23, 33, 31]]
print (len(A))
k=0
def get_under(A):#获取A的下三角矩阵
    Under=list(np.zeros((len(A),len(A))))
    for i in A:
        x=A.index(i)
        n=0
        for t in i:
            if n<=x:
                Under[x][n]=A[x][n]
            n=n+1
    d=[]
    for i in Under:
        d.append((list(i)))
    return d

def get_base(m):#给一个矩阵为基，在这个基上修改得到我们的答案
    base=list(np.zeros((len(A),len(A))))
    return base

def get_GT_D(a,base,k):#对于对角线上的元素有这样的算法
    m=0
    sum1=0.00000000000
    while m < k:
        sum1=sum1+(base[k][m])**2
        m=m+1
    base[k][k]=(a[k][k]-sum1)**(0.5000000000)
    return base

def get_GT_ND(a,base,i,k):#对于非对角线上的元素有这样的解法，应该可以和上面一部分并在一块
    if i==k:
        return base
    else:
        sum1=0.0000000000000
        m=0
        if k-1<0:
            base[i][k]=a[i][k]/base[k][k]
        else:
            while m<k:
                sum1=sum1+base[i][m]*base[k][m]
                m=m+1
            base[i][k]=(a[i][k]-sum1)/base[k][k]
        return base

def get_G(A):#导出我们需要的矩阵G
    a=get_under(A)
    base=get_base(A)
    base[0][0]=a[0][0]**0.50000000000
    n=[]
    for i in base:
        n.append(list(i))
    base=n
    i=0
    while i<len(A):
        k=0
        while k<i:
            get_GT_ND(a,base,i,k)
            k=k+1
        get_GT_D(a,base,k)
        i=i+1
    return base

def build_matrix(A,b):#通过这段代码导出增广矩阵
    B=[]
    for i in A:
        n=A.index(i)
        i.append(b[0][n])
        B.append(i)
    return B

def solve_lower(A,b):#解线性方程组的第一种方法，这里是Gy=b，顺序gauss消去法解出y
    B=build_matrix(get_G(A),b)
    C=[]
    for i in B:
        C.append(np.array(i))
    k=0
    while k<len(A):
        for i in range(k+1,len(A)):
            C[i]=C[i]-C[k]*B[i][k]/B[k][k]
        k=k+1
    D=[]
    for i in C:
        D.append(list(i))
    ans=[]
    for i in D:
        for j in i:
            if j==0:
                pass
            else:
                ans.append(i[-1]/j)
                break
    ans1=[]
    ans1.append(ans)
    return ans1

b= solve_lower(A,b)
N=np.mat(get_G(A)).T
ee=np.mat(b).T
print (N.I*ee) #解线性方程组的第二种方法，将系数矩阵的逆矩阵左乘到方程右端

    运行结果：