题面
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Note: m and n will be at most 100.
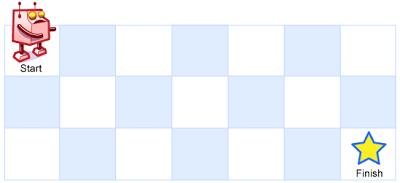
说白了就是:统计从二维数组左上角到右下角总共有多少不同路径。(0 <= m, n <= 100)
样例
Example 1:
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Right -> Down 2. Right -> Down -> Right 3. Down -> Right -> RightExample 2:
Input: m = 7, n = 3 Output: 28
思路
由于只能朝下或者右走,稍加推导,我们就可以看出:当前点的路径数就等于它左边点路径数加上上边点路径数,很容易想到递归(很不幸,层数过大,栈会溢出!)。so, 我们只能通过DP循环来做。
算法 : DP
时间复杂度:O(m*n)
空间复杂度:O(m*n)
1. 用二维数组还是一维数组记录状态都可以,我们先用二维来说明问题。即:创建二维数组dp[m][n]
2. 预处理第一行和第一列,因为第一行只能往右走,第一列只能往下走(只有一条路径,所以都初始化为1)
3. 遍历二维DP数组:当前点路径=上边点路径+左边点路径
状态方程:
dp[0][j] = 1
dp[i][0] = 1
dp[i][j] = dp[i-1][j] + dp[i][j-1]
源码
1 int uniquePaths(int m, int n) { 2 if(m == 0 || n == 0) 3 return 1; 4 int dp[n][m] = {0}; 5 dp[0][0] = 1; 6 for(int i=1; i<m; i++) 7 dp[0][i] = 1; 8 for(int i=1; i<n; i++) 9 dp[i][0] = 1; 10 for(int i=1; i<n; i++) 11 { 12 for(int j=1; j<m; j++) 13 { 14 dp[i][j] = dp[i][j-1] + dp[i-1][j]; 15 } 16 } 17 return dp[n-1][m-1]; 18 }
优化:空间优化
上面算法,我们使用了二维数组记录DP状态,其实用一维就够了。推到一个简单的例子你就会发现,焦点总是在一行上,只要用一行从上到下滑动,就可达到目的。
时间复杂度:O(m*n)
空间复杂度:O(n)
源码
1 int uniquePaths(int m, int n) { 2 //空间压缩 3 if(m == 0 || n == 0) 4 return 1; 5 int dp[m] = {0}; 6 for(int i=0; i<m; i++) 7 dp[i] = 1; 8 for(int i=1; i<n; i++) 9 { 10 dp[0] = 1; 11 for(int j=1; j<m; j++) 12 { 13 dp[j] = dp[j-1] + dp[j]; 14 } 15 } 16 return dp[m-1]; 17 }