uva3882

约瑟夫问题的变形

看了网上的题解，这题有一个trick就是每轮删完点后将剩下的点重新编号，从0编到n-1。

这样操作之后，我们就可以对删点前后的两个状态进行递推了。

假设我现在有一排点，编号为0到n-1，现在我从0开始数k个删掉第k个点，也就是删掉点k-1。

剩下的点为0，1，2……k-2，k……，n-1

我从k这个点开始重新编号，即：

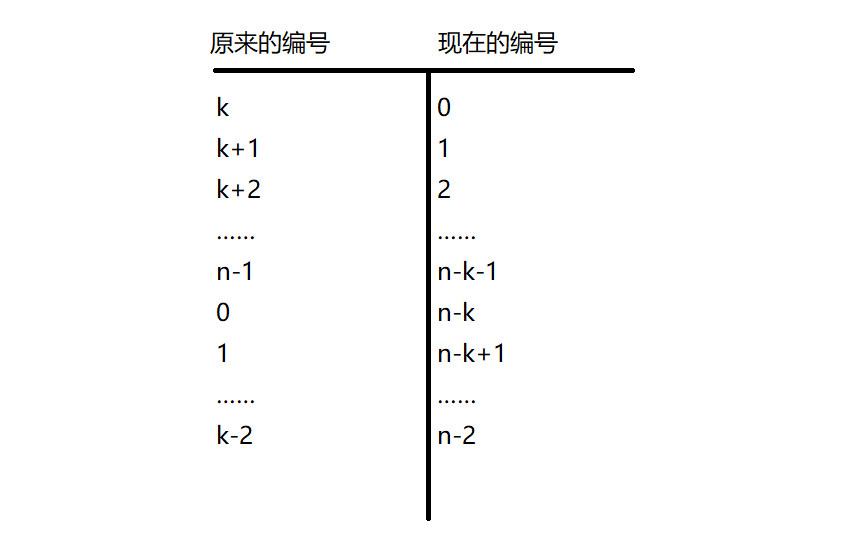
这样子问题具有相似性了。（因为同样是从0开始数到第k个删掉）

那么怎么递推呢？

可以看出，想要恢复上一轮的编号，只需要+k再整体%n即可

如果记f[n] = n个数从0开始编号数到第k个删掉最后剩下的数的编号的话，

f[n]  = (f[n-1] + k) % n;(注意这里的n是变化的)

最后输出（m-k+1+f[n]）%n。

这个式子拆成两部分来解释，一部分是+1：

因为我们设计的状态是从0开始的，然而题目是从1开始的，所以最后加1。

另一部分是m-k：

这是因为要删掉第m个，然而我们设计的状态是从0开始数k个删，这样如果我们加上m-k的话，就相当于成功地把m当成了第一个删的对象。（我们之前第一个删的对象是k嘛）（很难表达。。。见谅）

综上输出（m-k+1+f[n]）%n

最后如果答案小于0，还要加上n。

#include <cstdio>

using namespace std;

const int maxn = 10005;

int n, k, m;

int f[maxn];

int main()
{
    while(scanf("%d%d%d", &n, &k, &m) && n)
    {
        f[1] = 0;
        for (int i = 2; i <= n; i++)
            f[i] = (f[i - 1] + k) % i;
        int ans = (f[n] + m - k + 1) % n;
        if (ans <= 0) ans += n;
        printf("%d
", ans);
    }
    return 0;
} 

代码很简单，思路很复杂。