周赛200（暴力，模拟，贪心，动规）

class Solution {
    public int countGoodTriplets(int[] arr, int a, int b, int c) {
        int n = arr.length, res = 0;
        for(int i = 0; i < n - 2; i++) {
            for(int j = i + 1; j < n - 1; j++) {
                for(int k = j + 1; k < n; k++) {
                    if(Math.abs(arr[i] - arr[j]) <= a && Math.abs(arr[j] - arr[k]) <= b && Math.abs(arr[i] - arr[k]) <= c) res++;
                }
            }
        }
        return res;
    }
}

 

class Solution {
    public int getWinner(int[] arr, int k) {
        int n = arr.length;
        Deque<Integer> queue = new LinkedList<>();
        int res = 0;
        for(int num : arr) {
            queue.addLast(num);
            res = Math.max(res,num);
        }
        int cur = 0, sum = 1;
        while(true) {
            int num1 = queue.pollFirst(), num2 = queue.pollFirst();
            int min = Math.min(num1,num2), max = Math.max(num1,num2);
            if(max == res) return res; // 优化
            sum++;
            if(cur != max) {
                cur = max;
                sum = 1;
            }
            if(sum == k) break;
            queue.addLast(min);
            queue.addFirst(max);
        }
        return cur;
    }
}

 

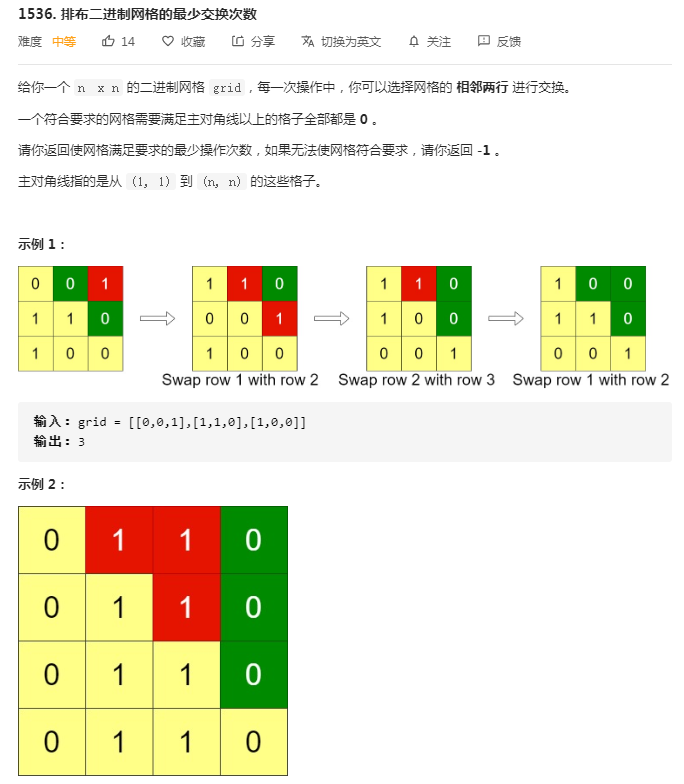
class Solution {
    public int minSwaps(int[][] grid) {
        int n = grid.length;
        LinkedList<Integer> queue = new LinkedList<>();
        for(int i = 0; i < n; i++) { // 预处理每行末尾0的个数
            int sum = 0;
            for(int j = n - 1; j >= 0; j--) {
                if(grid[i][j] == 0) {
                    sum++;
                } else {
                    break;
                }
            }
            queue.addLast(sum);
        }
        int res = 0;
        for(int i = 0; i < n - 1; i++) {
            int j = i + 1, step = n - i - 1;
            if(queue.get(i) >= step) continue; // 合格则跳过
            while(j < n) {
                if(queue.get(j) >= step) {
                    int sum = queue.remove(j);
                    queue.addFirst(sum);
                    res += j - i;
                    break;
                }
                j++;
            }
            if(j == n) return -1;
        }
        return res;
    }
}

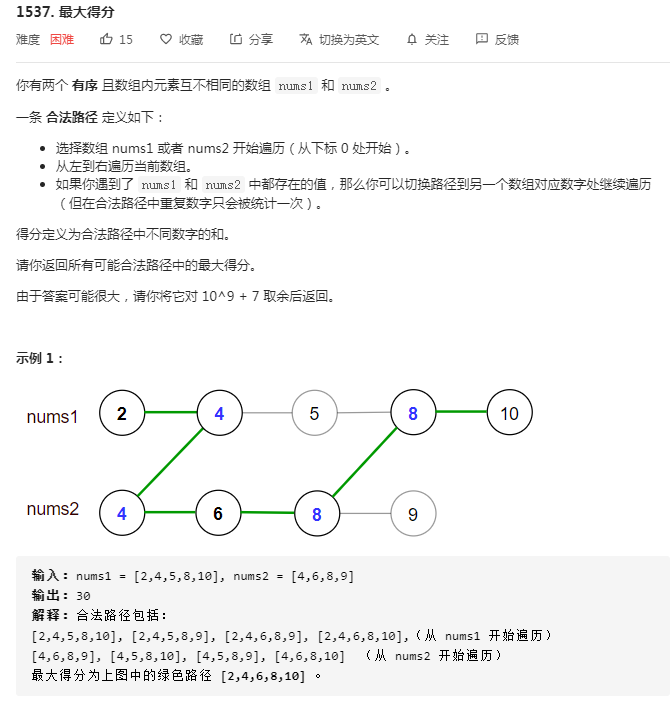
　　分析：

　　　　由于两个数组都是严格单调递增的，我们可以使用two pointers从小到大遍历两个数组。
　　　　其实还是DP的思想：dpx[i+1] 定义为以numsx[i]结尾的序列的最大和。
　　　　当两个元素相同的时候就有两种选择：dp1[i+1] = dp2[j+1] = max(dp1[i], dp2[j]) + nums1[i]
　　　　否则的话较小的那个元素往前走一步，只有一种选择：dpx[i+1] = dpx[i] + numsx[i]
　　　　时间复杂度：O(n)
　　　　空间复杂度：O(n) dp[i]只和dp[i-1]有关系，所以可以降维到O(1) 

class Solution {
    public int maxSum(int[] nums1, int[] nums2) {
        final int mod = 1_000_000_007;
        int m = nums1.length, n = nums2.length;
        long a = 0, b = 0;
        int i = 0, j = 0;
        while(i < m || j < n) {
            if(i < m && j < n && nums1[i] == nums2[j]) {
                a = b =  Math.max(a,b) + nums1[i];
                i++;
                j++;
            } else if (i < m && (j == n || nums1[i] < nums2[j])) {
                a += nums1[i++];
            } else {
                b += nums2[j++];
            }
        }
        return (int)(Math.max(a,b) % mod);
    }
}