1547. 切棍子的最小成本（区间dp）

 

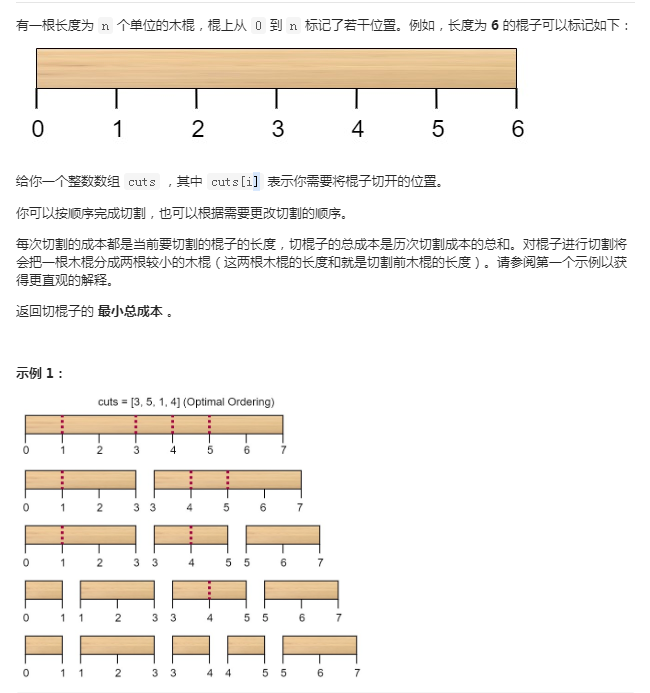
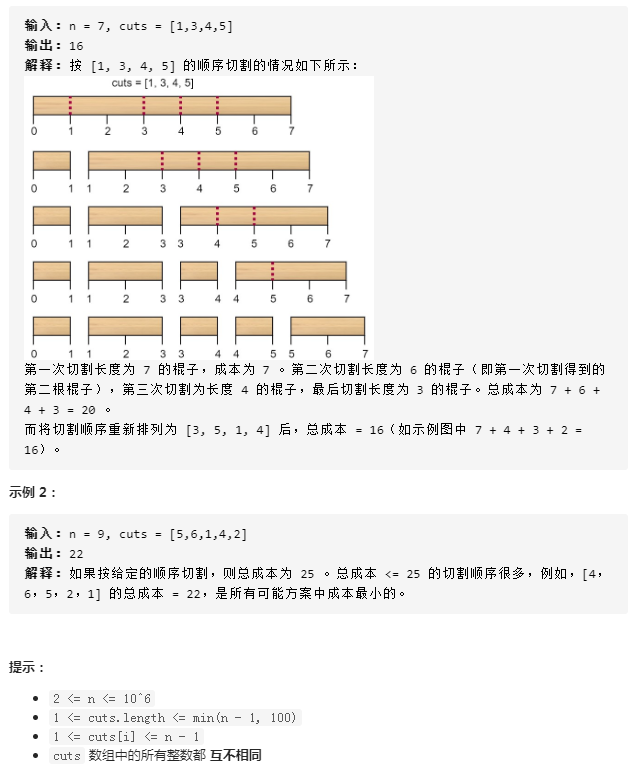
　　分析：将木棍的两个端点（0和n）加到cost数组中，dp[i][j]表示把这段木棍的第i到j个点完成切割的最小成本,i和j都是cost数组的下标。　　　　　

　　状态计算：

　　最后的合并位置是k

　　dp[i][j] = min(dp[i, k] + dp[k, j] + cost)

class Solution {
    public int minCost(int n, int[] cuts) {
        List<Integer> list = new ArrayList<>();
        list.add(0);
        list.add(n);
        for(int num : cuts){
            list.add(num);
        }
        Collections.sort(list);
        int m = list.size();
        int[][] dp = new int[m][m];
        for(int len = 2; len < m; len++){//枚举区间 
            for(int i = 0; i + len < m; i++){//枚举左端点
                int j = i + len;//右端点
                dp[i][j] = Integer.MAX_VALUE;
                // 枚举最后一个分割点
                for(int k = i+1; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + list.get(j) - list.get(i));
                }
            }
        }
        return dp[0][m-1];
    }
}