1579. 保证图可完全遍历（并查集）

 

 

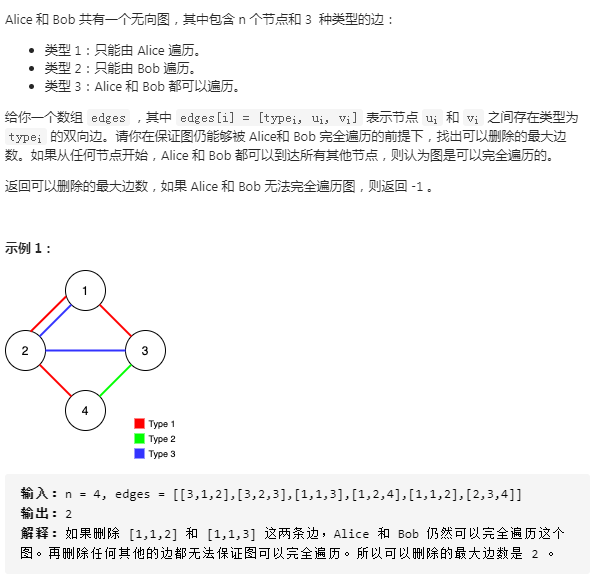
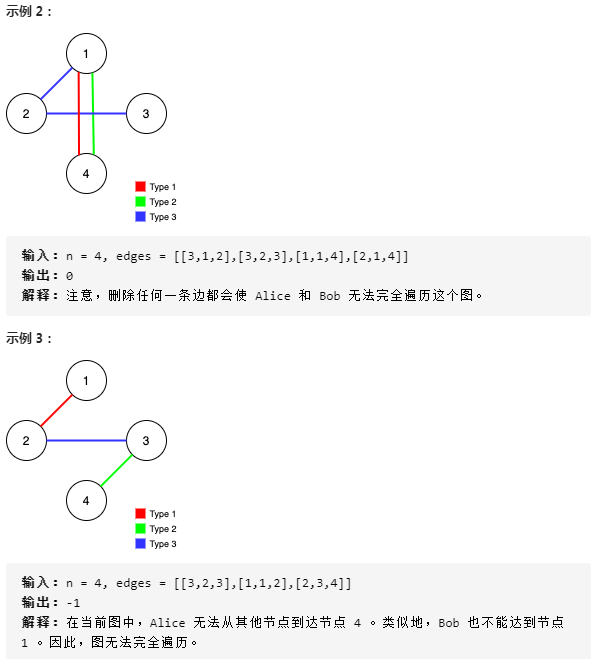
class Solution {

    int[] pa;
    int[] pb;

    public int find(int[] p, int x) {
        if(p[x] != x) p[x] = find(p,p[x]);
        return p[x];
    }

    public int maxNumEdgesToRemove(int n, int[][] edges) {
        int m = edges.length;
        pa = new int[n+1];
        pb = new int[n+1];
        for(int i = 1; i <= n; i++) {
            pa[i] = i;
            pb[i] = i;
        }
        int sizea = 0, sizeb = 0, res = 0;
        for(int[] e : edges) { // 优限遍历蓝边，两人都可以通过
            if(e[0] == 3) {
                int a = e[1], b = e[2];
                int fa = find(pa,a), fb = find(pa,b);
                int ffa = find(pb,a), ffb = find(pb,b);
                if(fa != fb) { // 先遍历蓝边两人是同步的，过不过得去是同步的
                    sizea++;
                    pa[fa] = fb;
                    sizeb++;
                    pb[ffa] = ffb;
                } else {
                    res++; // 已联通就删除这条变
                }
            }
        }
        for(int[] e : edges) { // 遍历红边
            if(e[0] == 1) {
                int a = e[1], b = e[2];
                int fa = find(pa,a), fb = find(pa,b);
                if(fa != fb) {
                    sizea++;
                    pa[fa] = fb;
                }
                else res++;
            }
        }
        for(int[] e : edges) { //遍历绿边
            if(e[0] == 2) {
                int a = e[1], b = e[2];
                int fa = find(pb,a), fb = find(pb,b);
                if(fa != fb) {
                    sizeb++;
                    pb[fa] = fb; 
                }
                else res++;
            }
        }
        if(sizea == n - 1 && sizeb == n - 1) {
            return res;
        } else {
            return  -1;
        }
    }
}