Fisher判别式（LDA）

Fisher判别式（LDA）

简介

上面从贝叶斯公式出发，得到了线性判别分析的公式，这里从另外一个角度来看线性判别分析，也就是常说的Fisher判别式。其实Fisher判别式就是线性判别分析（LDA），只是在讨论Fisher判别式的时候，更侧重于LDA的数据降维的能力。

在应用统计学方法解决模式识别、机器学习中的问题的时候，有一个问题总是会出现：维数问题。很多在低维空间里可以解析或者计算的算法，在高维空间里面往往行不通，因此，数据降维就成了处理实际问题中的关键。

单纯的从数学角度考虑，将dd维空间的数据压缩称为1维的数据是非常的容易的。然而，即便样本集合在dd维空间里形成若干紧凑的相互分得开的集合，当把它们投影到某一个直线上的时候，就可能使得这些样本混合在一起无法分别开来。但，在实践中发现，总可以找到某个方向，使得在这个方向的直线上，样本的投影能分开的最好。那么，现在的问题就是，如何根据实际情况找到这条最好的、最容易分类的投影线。这就是线性判别分析（Linear Discriminant Analysis）所要解决的基本问题，线性判别分析在很多时候，也叫做 Fisher’s linear discriminant（Fisher线性判别式）。准确的说，它是在Fisher线性判别式基础上的一个推广。

线性判别分析的基本思想，是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性，因此，它是一种有效的特征抽取方法。

在上面关于线性判别分析的说明中提到，投影后的样本在新的空间需要有最大的类间距离和最小的类内距离。那么，什么是类间距离？什么又是类内距离？线性判别分析又是如何在最大化类间距离的同时最小化类内距离？回答完了这三个问题，就基本上能对线性判别分析有一个基本的了解了。

类间距离

对于线性分类器，有一种观点就是将线性分类器看成是一个降维的操作。这里首先考虑二分类的问题，假设输入向量x是D维的，并使用下面这个变换，将x投影到一个一维的数据y上：

 

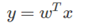
此时在y上加一个阈值−w₀，并以此来做二分类：

 

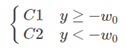
毫无疑问，上面的这种投影操作，会损失大量的样本信息，同时在投影的直线上，可能会使得各个类别的数据相互重叠，无法分别开来。但无论怎样，通过调整ww都可以找到一条最好的直线，使得投影之后类之间的距离能够最大。

一类的数据都像是一个云团，存在各自的分布，那么如何定义两个类之间的距离呢？这里可以先考虑两个类C1,C2各自的均值m1,m2：

 

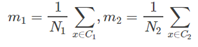
用两个均值m1,m2之间的距离m1−m2，作为类之间的距离，这是一种非常简单直观的类间距离的定义方法。

当两个类分别通过w做投影之后，那么投影之后的类间距离为：

 

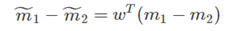
这里m˜₁ 是C1投影之后的类均值；m˜₂是C2投影之后的类均值。而我们要做的，就是要找一个w能够最大化m˜₁−m˜₂。但是，从上面的式子可以看出，通过增大w的模，可以无限的增大m˜₁−m˜₂，为了解决这个问题，需要将w的模设为1：||w||₂=1。也即是说，w的模并不重要，重要的是w的方向。

对上面的式子，使用拉格朗日乘子法：

 

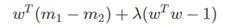
对w求导之后，得到：

 

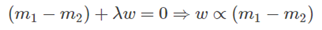
这个结果也是显然的，使用类的均值作为类间距离，要在投影的时候最大化类间距离，自然要让投影线和(m1−m2)平行。

但是，单纯最大化类间距离真的就可以让投影后类之间的重叠最少吗？看下面这幅图。这幅图是从PRML上截取下来的，这幅图左边就是单纯的最大化类间距离，所以左图中w和 (m1−m2)是平行的。右图是Fisher线性判别式(Fisher linear discriminant)得到的w。

 

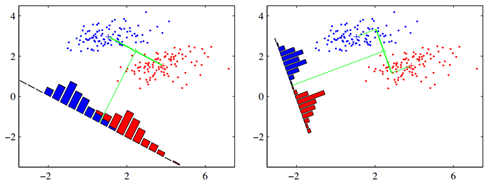
很显然相对于右图而言，单纯的最大化类间距离无法让投影后类的重叠最小，那么Fisher线性判别式到底又做了什么才能到到这个效果呢？这就是下面要讲的：最小化类内距离。

类内距离

对于一个存在一定的分布的类而言，我们用来定义这个类的类内距离，最常用的，就是方差（variance），方差所表示的，就是数据的离散程度。一个类Ck在w上投影之后，其类内方差为：

 

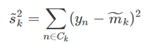
这里 y_n=w^Tx_n ，是x_n在w上的投影。

我们可以定义，投影后，总的类内方差为：投影后，各自类内方差的总和：s˜²₁+s˜²₂

Fisher线性判别式

上面已经介绍了类间距离，也就是类的均值的差；类内距离，也就是类内的方差。Fisher线性判别式的基本思想就是要最大化类间距离，同时最小化类内距离。这里就定义一个比值：

 

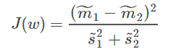
将这个比值最大化，就可以达到最大化类间距离的同时，最小化类内距离了。

对于原始的数据而言，其类内方差可以写为：

 

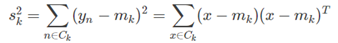
投影后的类内方差为：

 

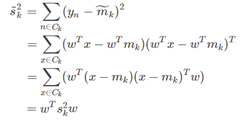
这里定义原始数据的类内总方差为:

 

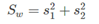
那么投影后的类内总方差为：

 

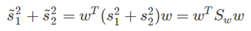
投影后，类间距离也可以写成相似的形式：

 

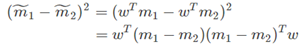
这里定义：

 

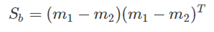
那么，投影后的类间距离可以写成为：

 

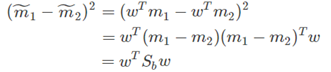
这样，就是可以把Fisher判别式的判别准则重写为下面这个形式：

 

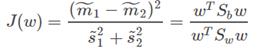
其中：

 

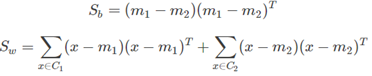
上面这个式子对w求导之后，可以得到：

 

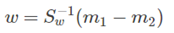
这样，我们就可以得到将投影后的类间距离最大化，同时投影后的类内距离最小化的之间ww。这样，就从一个DD维问题转化为了一个更容易分析和处理的一维问题。

当然，这个问题是一个多对一的问题，从理论上讲，在很多训练样本的情况下，这个方法不仅不能让最小误差率降低，甚至会在一定程度上提高误差率。然而，我们总还是愿意为了得到在一维中操作的方便性，而想要的牺牲一些理论上的分类效果。

此时，最后剩下的问题就是如何在投影后，求解阈值，来进行分类了。阈值点，就是在一维空间中，可以将两类分开的那个点的位置，这个问题相对来说非常的简单，这里不予讨论。

这里有一种特殊情况，就是当数据的条件概率分布函数p(x|Ck)是多远正太函数，并且各个类别的协方差矩阵Σ相同的时候，最佳的判别边界方程为：

 

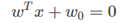
其中：

 

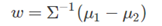
从上面的推导可以看出，Fisher判别式就是线性判别分析（LDA），只是在讨论Fisher判别式的时候，更侧重于LDA的数据降维的能力。

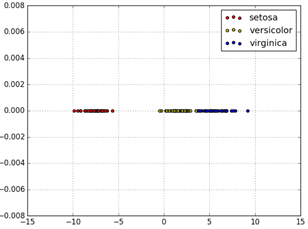
使用

# 将数据的特征维度降为一维

# 当然这里可以将n_components设置为任何小于原始特征维度的数目

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis(n_components=1)

X= lda.fit(X, y).transform(X)

Y= np.zeros(X_r2.shape)