逻辑回归
1)逻辑回归模型:(其中g是sigmoid函数)
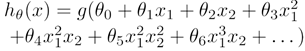
2)逻辑回归的损失函数是交叉熵损失函数,也叫Log损失,互熵损失:
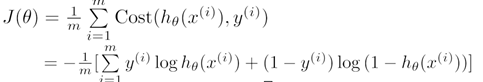
逻辑回归的损失函数为何不使用最小二乘法损失:
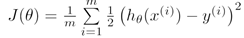
由上述最小二乘法损失函数可以知道,它是一个非凸函数,使用梯度下降算法无法求解到极小值。
3)逻辑回归的应用经验
(1)LR以概率的形式输出,可解释性强,可控度高,模型稳定,收敛性高,易于引入新特征,例如引入组合特征(FM,FFM)。
(2)训练速度比其他分类算法如GBDT,SVM快很多。
(3)常应用在CTR预估,推荐系统的learning to rank或者其他分类场景。
(4)LR模型对样本不均衡敏感,可以使用上采样或者下采样。采样后进行的预测结果,用作排序没有问题,但是如果用于判定,则应该需要还原,因为我们的模型的训练数据并非原始的,而是经过采样后的数据。
(5)模型训练前,应对数据做预处理,如去均值,正态化。
(6)数据离散化处理:如对于一个连续值的特征,可以将数据排序后等分成k份,即k个区间,然后使用one-hot编码的方式分解为稀疏的向量。
这种0,1向量内积运算速度快,计算结果方便存储,易扩展。同时离散化后,给线性模型带来了一点的非线性。
理解方式:如原来的θx,经过离散化处理后变为θ1x + θ2x + θ3x + …,因此带来了一定的非线性。
4)LR模型算法调优经验
(1)选择合适的正则化(L1,L2,L1+L2)
L2正则化更加准确一点,L1正则化在一定程度上可以减少特征的个数,因为训练得到的一些权重值为0,模型稍微不准确。
(2)正则化系数C
(3)收敛的阈值,迭代次数
(4)模型不均衡时,调整loss fanction给定不同的权重。
(4)Bagging或者其他的模型融合