离群点检测是发现与大部分其他对象显著不同的对象。大部分数据挖掘都将这种差异信息视为噪声而丢弃,然而在一些应用中,异常点数据可能蕴含着更大的研究价值。
应用:电信和信用卡的诈骗检测、贷款审批、电子商务、网络入侵和天气预报等领域。例如,可以利用离群点检测分析运动员的统计数据,来发现异常的运动员。
离群点的成因:
数据来源于不同的类、自然变异、数据测量、收集误差
离群点的类型:
|
分类标准 |
分类名称 |
分类描述 |
|
从数据范围 |
全局离群点和局部离群点 |
从整体看,某些对象没有利群特征,但从局部看,却有一定的离群性 |
|
从数据类型 |
数值型离群点和分类型离群点 |
这是以数据集的属性类型进行划分的 |
|
从属性的个数 |
一维离群点和多维离群点 |
一个对象可能有一个或者多个属性 |
离群点检测方法
1)基于统计:构建一个概率分布模型,并计算对象符合该模型的概率,把具有低概率的对象视为离群点。该方法的前提是知道数据集服从什么分布。
2)基于临近度:在数据对象之间定义邻近性度量,把远离大部分点的对象视为离群点。
3)基于密度:考虑数据集可能存在不同密度区域这一事实,离群点是在低密度区域中的对象
4)基于聚类:
(1)丢弃远离其他簇的小簇
该过程可以简化为丢弃小于某个最小阈值的所有簇。
这个方法可以和其他任何簇类技术一起使用,但是需要最小簇大小的阈值以及小簇与其他簇之间距离的阈值。而且这种方案对簇个数的选择高度敏感,使用这个方案很难将离群点得分附加到对象上。
(2)聚类首先聚类所有对象,然后评估对象属于簇的程度。
可以用对象到它的的簇中心的距离来度量属于簇的程度 。特别的,如果删除一个对象导致该目标的显著改进,则可将该对象视为离群点。
距离的两种评估方法:绝对距离:对象到簇中心的距离
相对距离:对象到簇中心的距离/簇中所有点到簇中心距离的中位数
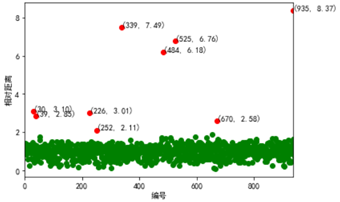
使用第二种方式来寻找离群点:
#-*- coding: utf-8 -*-
#使用K-Means算法聚类消费行为特征数据
import numpy as np
import pandas as pd
#参数初始化
inputfile = '../data/consumption_data.xls' #销量及其他属性数据
k = 3 #聚类的类别
threshold = 2 #离散点阈值
iteration = 500 #聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id') #读取数据
data_zs = 1.0*(data - data.mean())/data.std() #数据标准化
from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类,并发数4
model.fit(data_zs) #开始聚类
#标准化数据及其类别
r = pd.concat([data_zs, pd.Series(model.labels_, index = data.index)], axis = 1) #每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别'] #重命名表头
norm = []
for i in range(k): #逐一处理
norm_tmp = r[['R', 'F', 'M']][r[u'聚类类别'] == i]-model.cluster_centers_[i]
norm_tmp = norm_tmp.apply(np.linalg.norm, axis = 1) #求出绝对距离
norm.append(norm_tmp/norm_tmp.median()) #求相对距离并添加
norm = pd.concat(norm) #合并
import matplotlib.pyplot as plt
norm[norm <= threshold].plot(style = 'go') #正常点
discrete_points = norm[norm > threshold] #离群点
discrete_points.plot(style = 'ro')
for i in range(len(discrete_points)): #离群点做标记
id = discrete_points.index[i]
n = discrete_points.iloc[i]
plt.annotate('(%s, %0.2f)'%(id, n), xy = (id, n), xytext = (id, n))
plt.xlabel(u'编号')
plt.ylabel(u'相对距离')
plt.show()