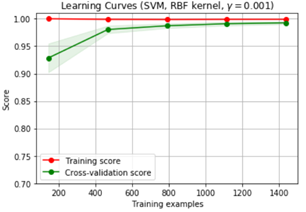
模型状态
过拟合和欠拟合
过拟合:在训练集上的准确率较高,而在测试集上的准确率较低
欠拟合:在训练集和测试集上的准确率均较低
学习曲线(Learning Curves)
1)概念概述
学习曲线就是通过画出不同训练集大小时训练集和交叉验证的准确率,可以看到模型在新数据上的表现,进而来判断模型是否方差偏高或偏差过高,以及增大训练集是否可以减小过拟合。
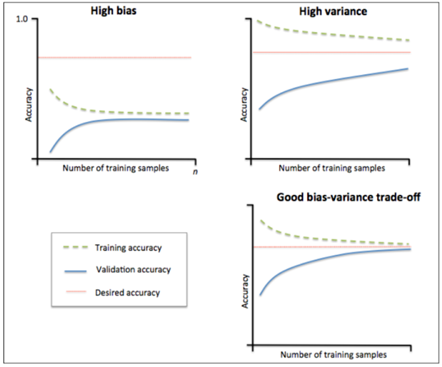
先明确两个概念:
偏差:指的是分类器对训练集和测试集的准确率与基准分类器的准确率有比较大的差距,是分类器与其他分类器的比较
方差:指的是分类器对训练集的准确率和测试集的准确率有比较大的差距,是分类器自身的比较
当训练集和测试集的准确率收敛且都收敛到较低准确率时,与基准分类器(红线表示)相比为高偏差。
左上角表示分类器的偏差很高,训练集和验证集的准确率都很低,很可能是欠拟合。
我们可以增加模型参数,比如,构建更多的特征,减小正则项。
此时通过增加数据量是不起作用的。
训练集和测试集的准确率与基准分类器有差不多的准确率,说明偏差较低,但在测试集和训练集的准确率差距较大,为高方差。
当训练集的准确率比其他独立数据集上的测试结果的准确率要高时,一般都是过拟合。
右上角方差很高,训练集和验证集的准确率相差太多,应该是过拟合。
我们可以增大训练集,降低模型复杂度,增大正则项,或者通过特征选择减少特征数。
理想情况是是找到偏差和方差都很小的情况,即收敛且误差较小。
2)学习曲线的绘制:高偏差和高方差
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
#对于朴素贝叶斯,shape(train_sizes)=(1,5),shape(train_scores)=(5,100),shape(test_scores)=(5,100)
#对于支持向量机,shape(train_sizes)=(1,5),shape(train_scores)=(5,10),shape(test_scores)=(5,10)
train_sizes, train_scores, test_scores = learning_curve( estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
#颜色填充,宽度是2倍的标准差
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,test_scores_mean + test_scores_std, alpha=0.1, color="g")
#绘制折线图
plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="Cross-validation score")
plt.legend(loc="best")
return plt
digits = load_digits()
X, y = digits.data, digits.target
#高偏差示例:朴素贝叶斯
title = "Learning Curves (Naive Bayes)"
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)
#高方差示例:SVM
title = "Learning Curves (SVM, RBF kernel, $gamma=0.001$)"
#定义交叉验证
cv = ShuffleSplit(n_splits=15, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)
plt.show()