时间序列的理论
u 平稳时间序列
时间序列平稳性定义:

平稳时间序列分为:自回归模型,滑动平均模型,自回归滑动平均模型
自回归模型:当前值由前p期值决定

滑动平均模型:

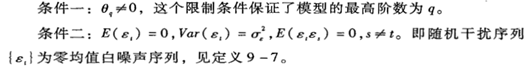
自回归滑动平均模型:

根据模型的自相关图,AR(p)模型的自相关系数随着延迟阶数的增加逐渐递减,呈现拖尾状态,而偏自相关系数随着延迟阶数的增加迅速减到0,呈现截尾状态。MA(q)模型与AR(p)模型相反。ARMA模型自相关和偏自相关图均是拖尾的。
模型的拖尾性和截尾性:

u 非平稳时间序列:

k阶差分
一阶差分:相距一期的两个序列之间的减法运算称为一阶差分运算
二阶差分:对一阶差分后序列再进行一次一阶差分运算称为二阶差分
k步差分:
相距k期的两个序列值之间的减法运算称为k步差分运算
差分方式的选择:
实践中,我们会根据序列的不同特点选择合适的差分方式,常见情况有如下三种:
(1)具有显著线性趋势的序列,通常一阶差分可以实现差分后平稳。
(2)具有曲线趋势的序列,通常低阶(二阶或者三阶)差分可以实现差分后平稳。
(3)具有固定周期的序列,通常进行步长为周期长度的差分运算,可以实现差分后平稳。

平稳时间序列的建模
u 平稳序列建模步骤
假如某个观察值序列通过序列预处理可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列进行建模。建模的基本步骤如下:
(1)求出该观察值序列的样本自相关系数(ACF)和样本偏自相关系数(PACF)的值。
(2)根据样本自相关系数和偏自相关系数的性质,选择适当的ARMA(p,q)模型进行拟合。
(3)估计模型中位置参数的值。
(4)检验模型的有效性。如果模型不通过检验,转向步骤(2),重新选择模型再拟合。
(5)模型优化。如果拟合模型通过检验,仍然转向不走(2),充分考虑各种情况,建立多个拟合模型,从所有通过检验的拟合模型中选择最优模型。
(6)利用拟合模型,预测序列的将来走势。
u 代码实现:
#导入数据
discfile = 'd:/data/arima_data.xls'
forecastnum = 5
#读取数据,指定日期列为指标,Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(discfile, index_col = u'日期')
data = pd.DataFrame(data,dtype=np.float64)
data
#时序图
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
data.plot()
plt.show()
#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
>>>观察自相关图可以看出是非平稳序列
#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print( ADF(data[u'销量']))
>>>
(1.813771015094526, 0.9983759421514264, 10L, 26L, {'5%': -2.981246804733728, '1%': -3.7112123008648155, '10%': -2.6300945562130176}, 299.46989866024177)返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
#由上面时间序列平稳性检验结果可知是非平稳时间序列
如何确定该序列能否平稳呢?主要看:
- 1%、%5、%10是不同程度拒绝原假设(原假设是存在单位根,即非平稳)的统计值,与ADF进行比较,ADF小于1%就可以极显著的拒绝原假设,即说明数据是平稳的。
- P-value是否非常接近0.05,小于0.05,是拒绝原假设,即时间序列是平稳的
#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plt.show()
#自相关图
plot_acf(D_data).show()
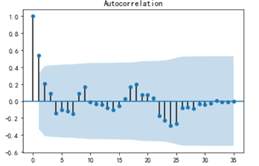
由自相关图可以知道时间序列是1阶截尾
#偏自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show()

由偏自相关图可以知道序列是拖尾的
ADF(D_data[u'销量差分'])#平稳性检测
#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(D_data, lags=1) #返回统计量和pvalue值
>>>
(array([11.30402222]), array([0.00077339])) #pvalue值远小于0.05,序列是非白噪声的
如何判断是否是白噪声序列?
原假设是序列是白噪声序列,我们只看pvalue值,如果值小于0.05,就拒绝原假设,即时间序列是非白噪声的
总结:根据上面的自相关图和偏自相关图,能够大概估计出模型是ARIMA(0,1,1),这种观察图的方法误差较大
下面使用更科学的方法:根据信息准则判断
#定阶
from statsmodels.tsa.arima_model import ARIMA
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try: #存在部分报错,所以用try来跳过报错。
tmp.append(ARIMA(data, (p,1,q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp) # bic_matrix是一个二维的矩阵
#从中可以找出最小值
bic_matrix = pd.DataFrame(bic_matrix)
p,q = bic_matrix.stack().idxmin() #先用stack展平,然后用idxmin找出最小值位置。
#打印最小值对应的p值和q值
print(u'BIC最小的p值和q值为:%s、%s' %(p,q))
#建立ARIMA(0, 1, 1)模型
model = ARIMA(data, (0,1,1)).fit()
#给出一份模型报告
model.summary()
#作为期5天的预测,返回预测结果、标准误差、置信区间。
model.forecast(5)