在介绍堆排序之前,先介绍一下堆这种数据结构:
堆是一颗完全二叉树,且具有如下性质,每个结点的值都大于等于其左右孩子结点的值,称为大顶堆;每个结点的值都小于等于其左右孩子结点的值,称为小顶堆。
我们以大顶堆为例来介绍堆排序,且采用顺序存储结构(物理结构)数组来存储堆的层序遍历结果。
堆排序的基本思想:将待排序的n个记录构造成一个大顶堆,将根结点与堆数组的倒数第一个元素交换位置,得到最大值;将剩余的(n-1)个记录调整为大顶堆,将根结点与堆数组的倒数第二个元素交换位置,得到次最大值;如此反复执行,最终可以将一个顺序表排为有序表。
以顺序表L = {3,1,5,9,8}为例,length = 5,下标从1开始。
堆排序的步骤:(1)对于顺序表L,调用调整堆算法将其构建为一个大顶堆;
(2)输出堆顶记录以后,调用调整堆算法将剩余记录调整为一个大顶堆,如此反复执行。
堆排序代码如下所示:
1 //堆排序算法
2 //将待排序的序列构造成一个大顶堆
3 //将大顶堆的根结点与堆末尾元素交换(层序遍历的最后一个结点)
4 //将剩余的序列重新调整为一个大顶堆
5 //将大顶堆的根结点与堆末尾元素交换
6 //如此反复执行
7 void HeapSort(SqList* L)
8 {
9 int i,j;
10
11 //结点i = 1... (length / 2);都是有孩子的结点
12 //构造大顶堆的过程,就是将每个非叶子结点当作根结点,将其和其子树调整为大顶堆的过程
13 //叶子结点均满足堆的定义
14 for (i = L->length / 2; i > 0; i--)//将L中的记录构造成一个大顶堆
15 HeapAdjust(L, i, L->length);//调用调整堆算法
16
17 for (j = L->length; j > 1; j--)
18 {
19 //将堆顶记录和堆尾记录交换位置
20 swap(L, 1, j);
21
22 //将剩余的序列重新调整为一个大顶堆
23 //除了根结点以外,均满足堆的定义,符合调用调整堆算法的条件
24 HeapAdjust(L, 1, j - 1);
25 }
26 }
顺序表中的记录变化如下:
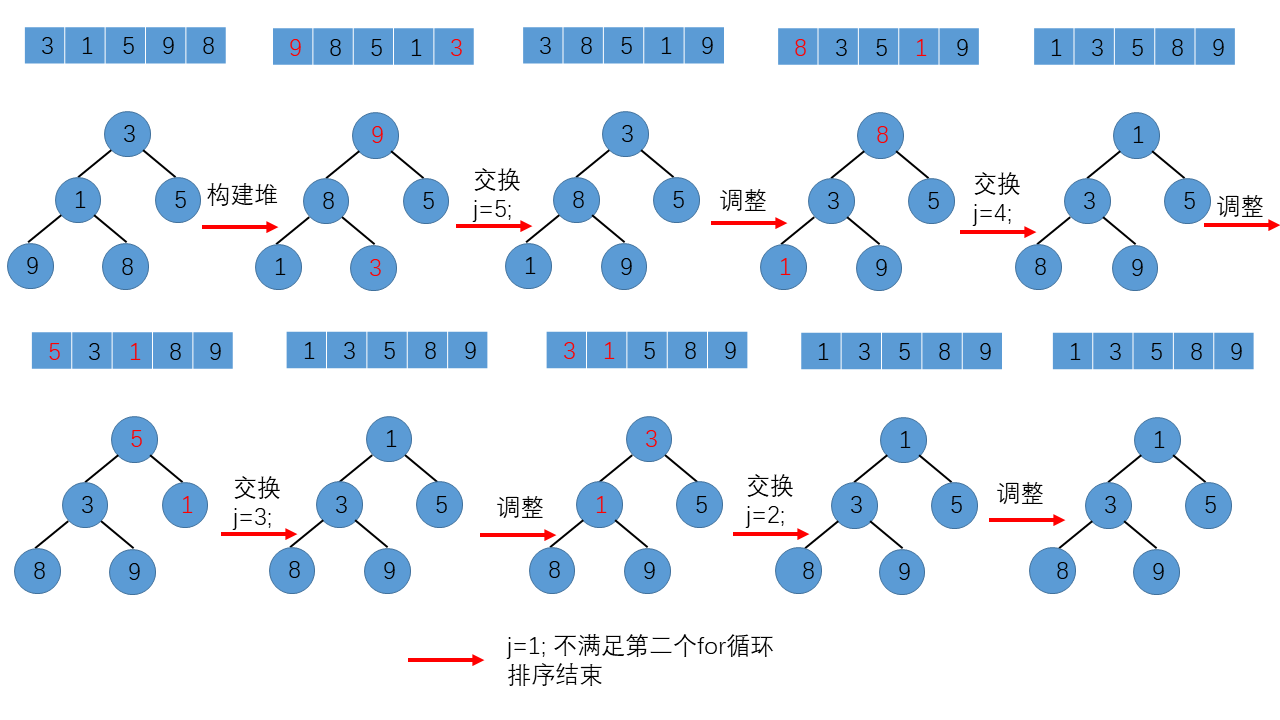
其实,堆排序的原理还是很简单明朗的,重点在于如何对堆进行调整。在调整堆算法中,要求待调整的完全二叉树除了根结点以外,其余部分均满足堆的性质。在调用调整堆算法构建堆的过程中,对于一棵完全二叉树,只有叶子节点一定满足堆的定义,其他子树不一定满足,所以我们选择从层序遍历中序号最大的且有孩子结点的结点开始,依次调用调整堆算法,直到到达完全二叉树的根结点,最终,将一个顺序表构建成一个大顶堆。总而言之,构建大顶堆的过程,就是从下往上,由右至左,将每个非叶子节点当作根结点,将其和其子树调整成大顶堆的过程。
调整堆代码如下所示:
1 //调整堆算法
2 //L中的记录除L->r[s](根结点)外均满足堆的定义
3 //调整L->r[s]的位置,使L->r[s,...m]成为一个大顶堆
4 void HeapAdjust(SqList* L, int s, int m)
5 {
6 //temp当作中间变量,存储根结点的值
7 int temp, j;
8 temp = L->r[s];//temp初始化为根结点的值
9
10 //结点j为结点(2*j)和结点(2*j+1)的双亲
11 //第x次for循环找出当前根结点的孩子结点的最大值,并赋值给当前根结点
12 for (j = 2 * s; j <= m; j *= 2)
13 {
14
15 //j < m说明还未到达最后一个结点
16 //若j <= m ,则r[j + 1]超出了索引范围
17 //L->r[j] < L->r[j + 1]表示沿着关键字较大的结点的方向向下筛选
18 if (j < m && L->r[j] < L->r[j + 1])
19 ++j;//j为关键字较大的结点的下标
20
21 if (temp >= L->r[j])//根节点的值大于等于其孩子结点的最大值
22 break;//跳出for循环
23
24 //当前根节点的值小于其孩子结点的最大值
25 L->r[s] = L->r[j];//当前根结点的孩子结点的最大值赋值给当前根结点
26
27 s = j;//关键字最大的孩子结点当作新的根结点
28 }
29
30 //将原来的根结点放在了正确的位置
31 L->r[s] = temp;
32 }
我们以调用调整堆算法构建堆的过程为例,来说明调整堆代码的实现流程,顺序表中的记录变化如下:
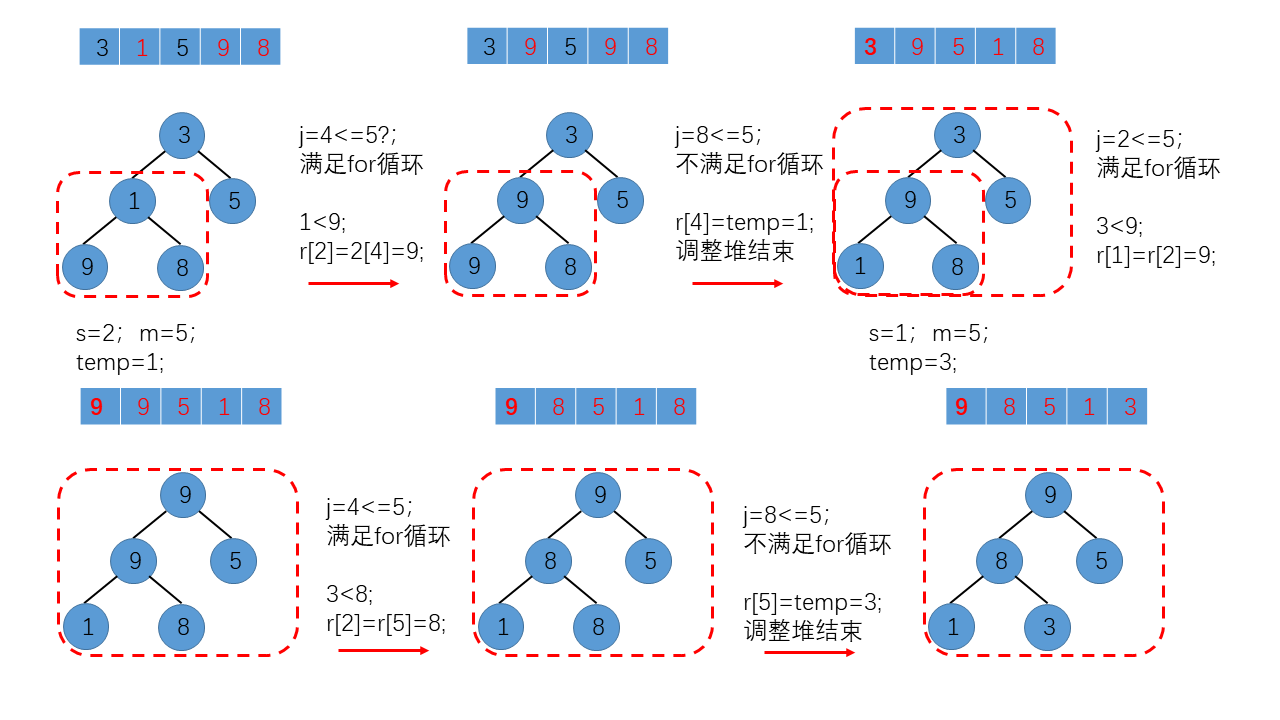
注意,红色虚线框内的部分为需要调整为堆的完全二叉树。如上图所示,为for循环条件不满足导致for循环结束的情况,与上述例子相同;为了说明另一种for循环结束的情况(break导致),我们以顺序表L = {8,1,5,9,3}为例,并做了图示说明。
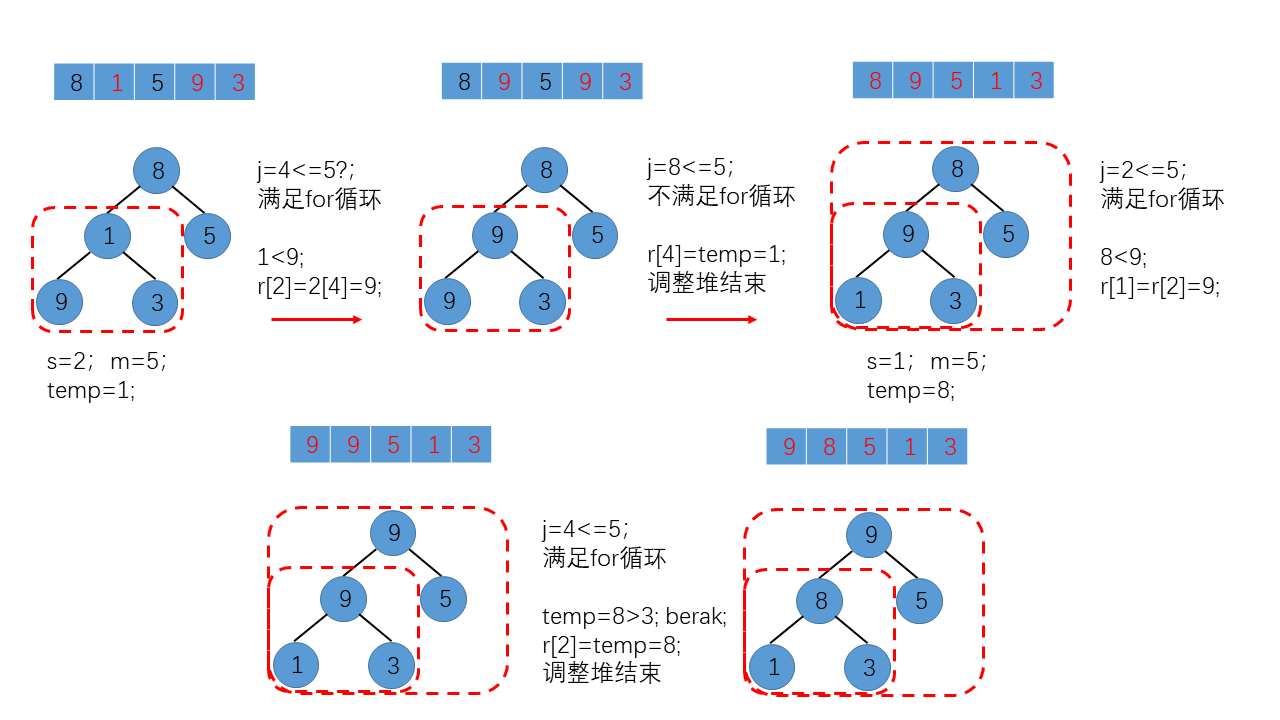
相关链接:
冒泡排序 https://www.cnblogs.com/yongjin-hou/p/13858510.html
简单选择排序 https://www.cnblogs.com/yongjin-hou/p/13859148.html
直接插入排序 https://www.cnblogs.com/yongjin-hou/p/13861458.html
希尔排序 https://www.cnblogs.com/yongjin-hou/p/13866344.html
归并排序 https://www.cnblogs.com/yongjin-hou/p/13921147.html
快速排序 https://www.cnblogs.com/yongjin-hou/p/13950379.html
参考书籍:程杰 著,《大话数据结构》,清华大学出版社。