题目描述
一列火车n节车厢,依次编号为1,2,3,…,n。每节车厢有两种运动方式,进栈与出栈,问n节车厢出栈的可能排列方式有多少种。
输入
一个数,n(n<=60000)
输出
一个数s表示n节车厢出栈的可能排列方式
样例输入
3
样例输出
5
典型的卡特兰数例子,但是阶乘要用质因数分解(算术基本定理)来算,不然会T
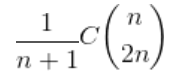 将上下阶乘质因数分解,然后约掉相同的质因数之后再乘,最后再除 n+1
将上下阶乘质因数分解,然后约掉相同的质因数之后再乘,最后再除 n+1
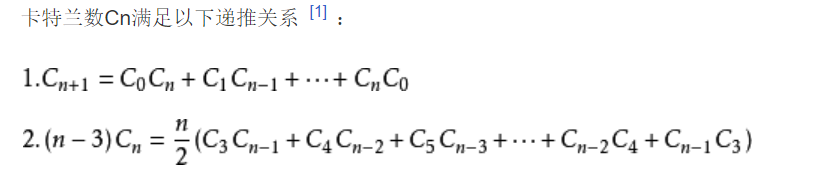
参考代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 2e5 + 10;
int f[maxn];
int main()
{
int n;
cin >> n;
f[0] = f[1] = 1;
for (int i = 2; i <= n; i++)
for (int j = 0; j < i; j++)
f[i] += f[j] * f[i - j - 1];
cout << f[n];
return 0;
}