015 冰冻集合的内置方法

简介

• 英文名：frozenset()
• 元素要求：必须是可哈希的
• 使用限制：不能随意增减自身的元素
• 集合集内部的集合必须是冻结集合
• 返回
  • 返回一个新的 set 或 frozenset
  • 若不提供任何参数，则返回一个新的空集

查看

• dir(frozenset): 列出 frozenset 的方法
• help(frozenset): 查看开发者对 frozenset 方法所编写的详细描述文档
  • help(set.copy) 可以仅查看 copy() 的用法

copy()

• 释义：返回一个浅拷贝

>>> f1 = frozenset({1, 2, 3})
>>> f2 = f1.copy()
>>> id(f1)
2040420701120
>>> id(f2)
2040420701120

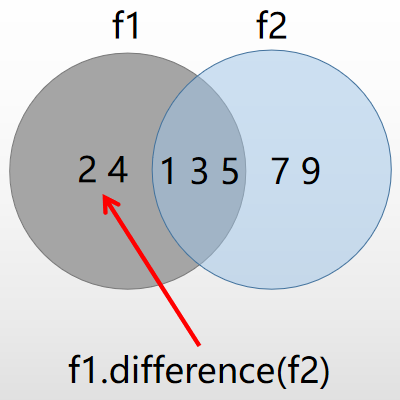
difference()

• 释义
  • 将两个或更多集合的差异作为新集合返回
  • • A.difference(B) 返回 A 中不同于 B 的元素
  • 与 set.difference() 一个意思，也可以想成概率论中的 A-B

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({1, 2, 3, 4, 5})
>>> f3 = frozenset({1, 2, 3})
>>> f1.difference(f2)
frozenset()
>>> f1.difference(f3)
frozenset({4, 5})
>>> f3.difference(f1)
frozenset()
>>> 
>>> s = {1, 2, 3}
>>> f1.difference(s)
frozenset({4, 5})
>>> 

intersection()

• 释义
  • 将两个集合的交集作为新集合返回
  • 与 set.intersection() 一个意思，也可以想成概率论中的 A∩B

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({6, 7, 8, 9, 0})
>>> f3 = frozenset({1, 2, 3})
>>> f1.intersection(f2)
frozenset()
>>> f1.intersection(f3)
frozenset({1, 2, 3})
>>> 
>>> s = {1, 2, 3}
>>> f1.intersection(s)
frozenset({1, 2, 3})
>>> 

isdisjoint()

• 释义
  • 检查两个集合的交集是否为空
  • 返回 True or False

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({6, 7, 8, 9, 0})
>>> f3 = frozenset({1, 2, 3})
>>> f1.isdisjoint(f2)
True
>>> f1.isdisjoint(f3)
False
>>> 
>>> s = {1, 2, 3}
>>> f1.isdisjoint(s)
False
>>> 

issubset()

• 释义
  • 与 issuperset() 相对
  • 检查此集合是否为另一个集合的子集
  • 返回 True or False

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({2, 3, 4})
>>> f3 = frozenset({4, 5, 6})
>>> f2.issubset(f1)
True
>>> f3.issubset(f1)
False
>>> 
>>> s = {1, 2, 3, 4, 5, 6}
>>> f1.issubset(s)
True
>>> 

issuperset()

• 释义
  • 与 issubset() 相对
  • 检查此集合是否为另一个集合的超集
  • 返回 True or False

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({2, 3, 4})
>>> f3 = frozenset({4, 5, 6})
>>> f1.issuperset(f2)
True
>>> f1.issuperset(f3)
False
>>> 
>>> s = {1, 2, 3}
>>> f1.issuperset(s)
True
>>> 

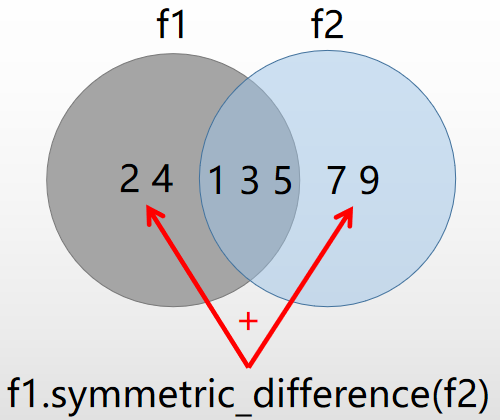
symmetric_difference()

• 释义：将两个集合的“对等差分”作为新集合返回

例1

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({1, 2, 3, 4, 5})
>>> f3 = frozenset({1, 2, 3})
>>> f1.symmetric_difference(f2)
frozenset()
>>> f1.symmetric_difference(f3)
frozenset({4, 5})
>>> 
>>> s = {1, 2, 3}
>>> f1.symmetric_difference(s)
frozenset({4, 5})
>>> 

例2

>>> f1 = frozenset({2, 4, 1, 3, 5})
>>> f2 = frozenset({1, 3, 5, 7, 9})
>>> f1.difference(f2)
frozenset({2, 4})
>>> f1.symmetric_difference(f2)
frozenset({2, 4, 7, 9})
>>> 

• difference() 输出的是自身与其它集合的不同之处

  

• symmetric_difference() 输出的是两个集合独有部分的并集

  

union()

• 释义：将集合的并集作为新集合返回

>>> f1 = frozenset({1, 2, 3, 4, 5})
>>> f2 = frozenset({4, 5, 6, 7, 8})
>>> f1.union(f2)
frozenset({1, 2, 3, 4, 5, 6, 7, 8})
>>> 
>>> s = {4, 5, 6, 7, 8}
>>> f1.union(s)
frozenset({1, 2, 3, 4, 5, 6, 7, 8})
>>>