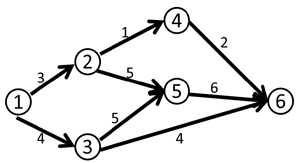
网络流的相关定义:
- 源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
- 汇点:另一个点也很特殊,只进不出,叫做汇点。
- 容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。很显然的,流量<=容量。而对于每个不是源点和汇点的点来说,可以类比的想象成没有存储功能的货物的中转站,所有“进入”他们的流量和等于所有从他本身“出去”的流量。
- 最大流:把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制,也就是,最大流。
求解思路:
首先,假如所有边上的流量都没有超过容量(不大于容量),那么就把这一组流量,或者说,这个流,称为一个可行流。
一个最简单的例子就是,零流,即所有的流量都是0的流。
- (1).我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。
- (2).那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
- (3).这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。
- (4).当找不到增广路的时候,当前的流量就是最大流,这个结论非常重要。
补充:
- (1).寻找增广路的时候我们可以简单的从源点开始做BFS,并不断修改这条路上的delta 量,直到找到源点或者找不到增广路。
- (2).在程序实现的时候,我们通常只是用一个c 数组来记录容量,而不记录流量,当流量+delta 的时候,我们可以通过容量-delta 来实现,以方便程序的实现。
最常用的算法之一是dinic,利用bfs从源点到汇点分层,然后dfs进行增广。