5 二叉树和递归

目录

1 二叉树

　LeetCode-104-二叉树的最大深度

　LeetCode-111-二叉树的最小深度

　LeetCode-226-翻转二叉树

　LeetCode-100-相同的树

　LeetCode-101-对称二叉树

　LeetCode-222-完全二叉树的节点个数

　LeetCode-110-平衡二叉树

2 递归的终止条件

　LeetCode-112-路径总和

　LeetCode-111-二叉树的最小深度

　LeetCode-404-左叶子之和

　LeetCode 257-二叉树的所有路径

　LeetCode 113-路径总和 II

　LeetCode-129-求根到叶子节点数字之和

3 更复杂的递归逻辑

　LeetCode 437-路径总和 III

4 二分搜索树

　LeetCode 235-二叉搜索树的最近公共祖先

　LeetCode 98-验证二叉搜索树

　LeetCode-450-删除二叉搜索树中的节点

　LeetCode-108-将有序数组转换为二叉搜索树

　LeetCode-230-二叉树的最近公共祖先

　LeetCode-236-二叉搜索树中第K小的元素

1 二叉树

二叉树具有天然的递归结构，可以从其定义上看，一棵二叉树就是其左右孩子都是一棵二叉树。对于一个递归方法而言都具有两部分：递归终止条件、递归过程。

例1：LeetCode 104。

class Solution {
    
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

 与此类似题目：LeetCode 111。

 例2：LeetCode·226。

class Solution {

    public TreeNode invertTree(TreeNode root) {
        if (root == null){
            return null;
        }
        // 反转左子树
        invertTree(root.left);
        // 反转右子树
        invertTree(root.right);
        // 将左右子树进行交换
        swap(root);
        return root;
    }
    // 上面的代码还是不过简洁，其实可以将交换操作放在递归中
    public TreeNode invertTree(TreeNode root) {
        if (root == null){
            return null;
        }
        // 保存右子树
        TreeNode rightTree = root.right;
        // 反转左右子树并交换
        root.right = invertTree(root.left);
        root.left = invertTree(root.right);
        return root;
    }
}

在这道题目中在交换的时候要注意区别引用，一开始在写交换的时候是下面的代码：

    //主方法中直接传入左右孩子    
    swap(root.left,root.right);

    private void swap(TreeNode left,TreeNode right) {
        TreeNode temp = left;
        left = right;
        right = temp;
    }

但这样的话其实没有修改root节点的引用，只不过是修改了左右孩子的引用，如下图所示，那么从root节点来看仍然是没有进行交换的。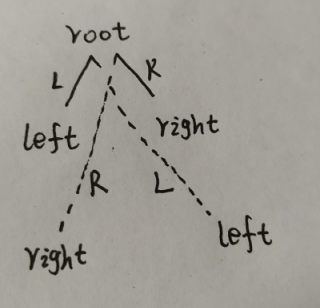

类似题目：LeetCode 100、101、222、110。

2 递归的终止条件

例1：LeetCode 112。根据题目的条件可以想出递归遍历左右子树直至sun为0即可，其代码如下：

class Solution {

    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null){
            return sum == 0;
        }
        if (hasPathSum(root.left,sum - root.left)){
            return true;
        }
        if (hasPathSum(root.right,sum - root.right)){
            return false;
        }
        return false;
    }
}

但上面的代码是错误的，当面对如下结构时就会产生误判，产生错误的主要原因就是递归时直接判断为空很有可能不是一个叶子节点因此要对递归的终止条件进行修改。

class Solution {

    public boolean hasPathSum(TreeNode root, int sum) {
        // 当直接传入一个空的树时
        if (root == null){
            return false;
        }
        if (root.right == null && root.left == null){
            return root.val == sum;
        }
        if (hasPathSum(root.left,sum-root.val)){
            return true;
        }
        if (hasPathSum(root.right,sum - root.val)){
            return false;
        }
        return false;
    }
}

 与此类似题目：LeetCode 111、404

例2：LeetCode 257。这里不再是简单的返回数值了，而是需要返回一个字符串。

class Solution {

    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        //递归的终止条件
        if (root.left == null && root.right == null){
            res.add(root.val+"");
            return res;
        }
        // 遍历左侧元素存入list集合中
        List<String> lefts = binaryTreePaths(root.left);
        // 遍历list集合
        for (int i = 0; i < lefts.size(); i++) {
            res.add(root.val+"->"+lefts.get(i));
        }
        // 遍历右侧元素存入list集合中
        List<String> rights = binaryTreePaths(root.right);
        // 遍历list集合
        for (int i = 0; i < rights.size(); i++) {
            res.add(root.val+"->"+rights.get(i));
        }
        return res;
    }
}

与此类似题目：LeetCode 113、129。

3 更复杂的递归逻辑

例1：LeetCode 437。本题中对路径的要求的更为宽泛，在前面的题目中采用的递归逻辑如下图所示，在左右子树递归时有sum-node.v其实已经默认了一个条件那就是节点node在路径中。

 在这道题目中直接采用上述递归肯定会有问题的，因此应该分类讨论：当这个节点在路径中时；这个节点不再路径中时。如下图所示：

class Solution {

    public int pathSum(TreeNode root, int sum) {
        //
        if (root == null){
            return 0;
        }
        // 包含root节点
        int res = findPath(root,sum);
        // 不包含root节点,只需要递归其左右子树即可
        res += pathSum(root.left,sum);
        res += pathSum(root.right,sum);

        return res;
    }
    // 在以node为根节点的二叉树中，寻找包含node节点的路径，和为num
    // 返回这样的路径个数
    private int findPath(TreeNode node, int num) {
        // 递归的终止条件
        if (node == null){
            return 0;
        }
        // 存储符合条件的路径的个数
        int res = 0;
        // 当找到符合条件的路径时不要立刻返回，因为节点中有负数可能后面还会有符合条件的路径
        if (node.val == num){
            res += 1;
        }
        // 在左子树中寻找
        res += findPath(node.left,num - node.val);
        // 在右子树中寻找
        res += findPath(node.right,num - node.val);

        return res;
    }
}

4 二分搜索树

定义：每个节点的键值大于左孩子，小于右孩子；以左右孩子为根的子树仍为二分搜索树。

例1：LeetCode 235。先对可能出现的情况进行讨论：当p和q在其同一侧时需要进行递归判断；当p和q一个大于node一个小于node时，node必然为其公共祖先；或者其祖先就是p或者q。

 

 

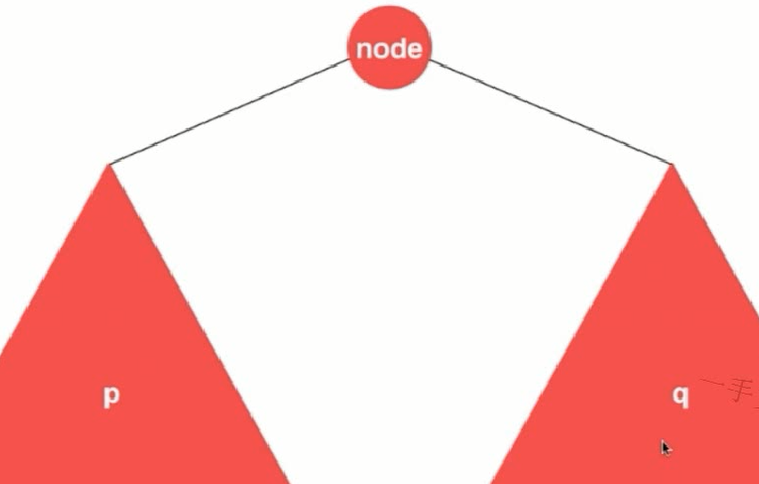
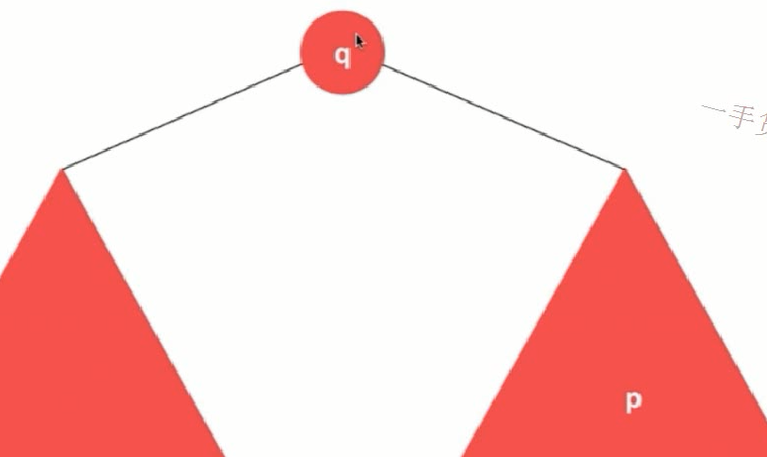
class Solution {

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 题目中已经明确说明p和q都在树中因此不用再检查了
        if (root == null){
            return null;
        }
        // 由二分搜索树的性质可知，当p和q均小于节点时必然在其左侧
        if (p.val < root.val && q.val < root.val){
            return lowestCommonAncestor(root.left,p,q);
        }
        // 由二分搜索树的性质可知，当p和q均大于节点时必然在其右侧
        if (p.val > root.val && q.val > root.val){
            return lowestCommonAncestor(root.right,p,q);
        }
        // 由二分搜索树的性质可知，当p和q一大一小时当前节点必然是其最近的公共祖先，因为递归的时候是从上向下的
        return root;
    }
}

 与此类似题目：LeetCode 98、450、108、230、236

0